Методика моделирования тепловизионных изображений

Методика моделирования  

тепловизионных изображений.

 

В теории и практике проектирования тепловизионных оптико-электронных систем немаловажную роль играет моделирование тепловизионных изображений. Яркость тепловизионных изображений зависит как от распределения температуры по поверхности наблюдаемого объекта, так и от коэффициента излучения и ориентации визируемых элементов его поверхности - его формы. Кроме того, качество тепловизионного изображения зависит от передаточных характеристик оптической системы и всех звеньев тепловизора.

В основу теории моделирования тепловизионных изображений заложен процесс формирования видеосигналов, пропорционально потоку теплового излучения объекта для всего тепловизионного кадра, в котором содержится L строк и N элементов в строке. Величина видеосигнала U( N, L ) элемента разложения кадра описывается выражением:

l₂

U ( N, L ) = ( 1/ p)×e (y)×w ×cosy(N,L)×dS(N,L)×ò S_l×W(l,T,y,z)×t₀(l)×t_a(l)×dl  ( 1 );

l₁

где  w  - передний апертурный угол оптической системы тепловизора;

y  - угол между нормалью к элементу dS( N,L ) поверхности объекта и направлением наблюдения;

W(l,T,y,z) - спектральная светимость элемента dS(N,L) поверхности объекта, имеющего абсолютную температуру T;

e(y) - индикатриса спектрального коэффициента излучения поверхности объекта;

S_l - абсолютная спектральная чувствительность приёмника излучения тепловизора;

l₁ ,l₂ - границы спектральной чувствительности приемника излучения;

t₀(l),t_a(l) - спектральный коэффициент пропускания оптической системы и слоя атмосферы;

y,z - координаты элемента dS(N,L) поверхности объекта в пространстве предметов [ 2 ] .

Для анализа влияния на качество изображения передаточных характеристик оптической системы тепловизора, приёмника излучения, электронного блока обработки информации и видеоконтрольного устройства (ВКУ) используется распределение освещённости E(y’, z’), которое определяется по формуле:

 

_{00 j×2×p×(n×y’+m×z’)}

E(y’, z’)= t₀×w’×òò L(n, m)×h₀(n,m)×h_п(n,m)×h_э(n,m)×h_в(n,m)×e dn×dm. (2)

^-00

где w’ - задний апертурный угол оптической системы тепловизора с интегральным коэффициентом пропускания t;

 h₀(n,m),h_п(n,m),h_э(n,m),h_в(n,m) - модуль передаточной характеристики соответственно оптической системы, приёмника излучения, электронного блока обработки информации и ВКУ тепловизора;

y’, z’ - координаты элемента dS поверхности объекта в пространстве изображений;

L(n,m) - пространственно-частотный спектр яркости поверхности объекта;

(n,m) - пространственные частоты, приведённые к плоскости изображений.

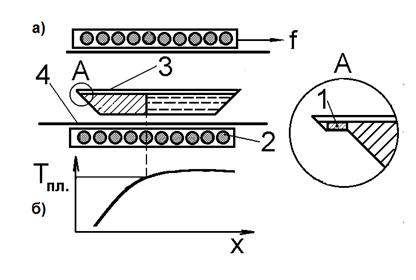
Тепловизионные методы в настоящее время широко используются в задачах распознавания и идентификации объектов. Но следует отметить, что пользуясь только обычными тепловизионными изображениями, величина видеосигналов в которых определяется выражением ( 1 ), распознать объекты внутри их контура практически невозможно. В чём причина потери информации о форме объекта внутри контура в обычных тепловизионных изображениях? Чтобы это выяснить рассмотрим рис.1. Согласно этому рисунку, справедливо равенство:

dS₁ × cos y₁ = dS ₂ × cos y₂ = dS₃ × cos y₃  ( 3 )

 

Анализируя рис.1 и эту связь, можно сделать вывод, что именно здесь и происходит потеря информации о форме объекта внутри контура. Сопряжённость всех элементов dS’ и dS, соответственно, приводит к тому, что площадки, расположенные под меньшими углами(yÞ0, cosyÞ1), должны иметь меньшие размеры dS, чтобы равняться тем площадкам, которые расположены под большими углами(yÞ90⁰, cosyÞ0).

В связи с этим становится ясной необходимость использования таких информационных оптических характеристик теплового излучения объектов, которые исключали бы пропорциональную связь параметров dS и cosy. К таким величинам относятся поляризационные свойства теплового излучения поверхности объектов. По этой причине и представляют интерес задачи моделирования и обработки поляризационных тепловизионных изображений.

2.Теория и методы моделирования поляризационных

тепловизионных изображений объектов.

 

2.1.Теория моделирования поляризационных тепловизионных

изображений на основе вектор-параметра Стокса теплового

излучения.

Для подробного описания теории моделирования поляризационных тепловизионных изображений рассмотрим объект произвольной формы, который в декартовой системе координат описывается уравнением:

f(x,y,z) = 0.

Допустим, что этот объект ( рис.2 ) наблюдается из точки Н, где расположен чувствительный элемент тепловизионной системы. Выбираем на поверхности этого объекта элемент dS, который соответствует одному элементу разложения кадра. Наклон площадки dS по отношению к элементу приёмника определяется

углом y между нормалью и направлением наблюдения r_н. Тогда векторы n и r_н  определяют плоскость наблюдения. Коэффициент излучения рассматриваемого объекта имеет две составляющие: параллельную e_ïï, которая лежит в плоскости наблюдения ( n*r_н ), и перпендикулярную e_ûë , которая перпендикулярна плоскости наблюдения. Положение элемента dS определяется в декартовой системе координат радиус-вектором R , а в сферической системе координат углами q и j.

Один из методов анализа поляризации пучка света - это метод вектор-параметра Стокса [ 3 ], характеризующий все виды и формы поляризации излучения поверхности объекта, который для нашего случая собственного излучения элементов dS(N, L) имеет вид:

é U₀ ( N, L) + U₉₀ ( N, L) ù

U_i( N, L ) =   ê U₀ ( N, L) - U₉₀ ( N, L) ê  , ( 4 )

ê U₄₅ ( N, L) - U₁₃₅ ( N, L) ç

ë 0    û

где i = 1, 2, 3, 4;

U₀, U₄₅, U₉₀, U₁₃₅  - величины сигналов, поляризованные, соответственно, под углами 0⁰, 45⁰, 90⁰, 135⁰ относительно плоскости референции ( плоскости отсчёта ).

Степень поляризации теплового изображения зависит от величины видеосигналов поляризационных составляющих тепловизионных изображений элементов поверхности объекта с азимута поляризации соответственно равны 0⁰, 45⁰, 90⁰, 135⁰. Величины видеосигналов U₀, U₉₀ в соответствии с тем, что коэффициент излучения e(y) можно представить в виде параллельной e_÷÷ и перпендикулярной e_ûë составляющих, запишем в виде:

U₀ (N, L) = A (N, L) ×[e_÷÷ (y) × (n * j)² + e_ûë(y) × (e_ûë × j)² ],  ( 5 )

 U₉₀ (N, L) = A (N, L) ×[e_÷÷ (y) × (n * k)² + e_ûë(y) × (e_ûë × k)² ]. ( 6 )

где  l₂

A ( N, L ) = ( 1/ p)×e (y)×w ×cosy(N,L)×dS(N,L)×ò S_l×W(l,T,y,z)×t₀(l)×t_a(l)×dl.

l₁

Тогда, например, зависимость степени поляризации теплового изображения, с азимутом t_n=0, от величины видеосигналов двух поляризационных тепловизионных изображений элементов поверхности объекта, с азимутами поляризации 0⁰, 90⁰, можно представить в виде:

P’ (N, L) = [ U₀ (N, L) - U₉₀(N, L)] / [U₀ (N, L)+U₉₀(N, L)], ( 7 )

где

P’ (N, L) - степень поляризации изображений с азимутом t_n=0.

Если пронумеровать вектор-параметр Стокса, то формула (4) примет вид:

é 1 ù

U₁(N, L) = U(N, L) ô P(N, L) ×cos2×t(N, L)    ê , ( 8 )

  ô P(N, L) ×sin2×t(N, L) ê

ë 0 û

где P(N, L) - степень поляризации излучения элемента dS(N, L) объекта;

t(N, L) - азимут поляризации излучения элемента dS(N, L).

На основе выражений (7) и (8) получим:

P’(N, L) = P(N, L) × cos2 ×t(N, L). ( 9 )

 

Подставив формулы (5) и (6) в выражение (7), получим следующее выражение для степени поляризации P’(N, L):

e_÷÷ (y)×[(n*j)² - (n*k)²] + e_ûë(y)×[(e_ûë*j)² - (e_ûë*k)²]

P’(N, L) = ------------------------------------------------------------------ , ( 10 )

e_÷÷ (y)×[(n*j)² + (n*k)²] + e_ûë(y)×[(e_ûë*j)² + (e_ûë*k)²]

где j , k - единичные орты координатных осей OY и OZ;

e_ûë, e_÷÷  - единичные векторы, соответственно, параллельной и перпендикулярной компонент коэффициента излучения элемента dS.

Преобразуем выражение (10) в виде:

[e_÷÷ (y)/e_ûë ]×[(n*j)² - (n*k)²] + [(e_ûë*j)² - (e_ûë*k)²]

P’(N, L) = ------------------------------------------------------------------ , ( 11 )

[e_÷÷ (y)/e_ûë ]×[(n*j)² + (n*k)²] + [(e_ûë*j)² + (e_ûë*k)²]

Принимая во внимание выражение:

P(y) =[ e_÷÷ (y) - e_ûë (y)] / [ e_÷÷ (y) + e_ûë (y)] ,

получим связь величин e_÷÷ (y) и e_ûë (y) со степенью поляризации P(y):

 

e_÷÷ (y)/e_ûë (y)= [1+ P(y)] / [1- P(y)]. ( 12 )

Анализируя данные исследований степени поляризации различных материалов, индикатрису P(y) можно представить в виде зависимости:

P(y) = a × (1- cosy),

где а - параметр, зависящий от типа и шероховатости материала.

Принимая во внимание, что косинус угла y между нормалью к элементу dS и единичным вектором наблюдения r_н  определяется как скалярное произведение этих векторов, получим:

P(y) = [ 1-(n*r_н) ] × a . ( 13 )

Подставив это выражение в формулу (12) получим:

e_÷÷ (y) 1+ [ 1 - (n*r_н)] × a

--------- = ------------------------- . ( 14 )

e_ûë (y) 1 - [ 1 - (n*r_н)] × a

Тогда, с учётом соотношения (12), из формулы (11) получим основное уравнение, выражающее зависимость между степенью поляризации P’(N, L) и формой объекта через функцию распределения нормали n для каждого элемента поверхности объекта:

1+ [ 1 - (n*r_н)] × a

------------------------ [(n*j)² - (n*k)²] + [(e_ûë*j)² - (e_ûë*k)²]

1- [ 1 - (n*r_н)] × a

 P’(N, L) = ---------------------------------------------------------------------- . ( 15 )

1+ [ 1 - (n*r_н)] × a

------------------------- [(n*j)² - (n*k)²] + [(e_ûë*j)² + (e_ûë*k)²]

1- [1 - (n*r_н)] × a

С помощью этой формулы можно определить степень поляризации всех элементов наблюдаемой тепловизором части поверхности объекта любой формы. Для этого нужно знать направление нормали n для каждого элемента поверхности в зависимости от его положения в декартовой системе координат. Оно определяется как оператор Гамильтона ( набла-оператор ) от функции f(x,y,z) = 0, описывающий форму объекта:

[( df/dx ) × i + ( df/dy ) × j + ( df/dz ) × k ]

n = ---------------------------------------------------- . ( 16 )

[( df/dx )² + ( df/dy )² + ( df/dz )² ] ^1/2

Единичный вектор наблюдения r_н определяется как разница векторов l и R по формуле:

 

r_н = ( l - R ) / | ( l - R ) |,  ( 17 )

 

где l - вектор, определяющий положение декартовой системы координат по отношению к точке наблюдения H;

R - радиус-вектор элемента dS поверхности объекта, определяющий его положение в декартовой системе координат x, y, z с единичными ортами i, j, k.

Радиус-вектор задаётся R формулой :

R = x × i + y × j + z × k . ( 18 )

Если направление наблюдения центра декартовой системы координат выбрано вдоль оси х, то есть направление вектора l и оси х совпадают, то вектор l выразится в виде:

l = l × i , ( 19 )

где l - расстояние от центра декартовой системы координат О до точки наблюдения Н;

i - единичный орт оси ОХ .

В этом случае выражение (17) примет вид:

r_н = [( l-x)i + y × j +z × k ] / [( l-x)²+ y² + z²]^1/2 . ( 20 )

Вектор перпендикулярной составляющей коэффициента излучения e_ûë перпендикулярен плоскости, определяемой векторами n и r_н ( плоскости наблюдения ), и находится как векторное произведение этих векторов по формуле:

 e_ûë = [ n* r_н ] / | [ n* r_н ] | . ( 21 )

 

Таким образом, определив степень поляризации P’ от всех элементов видимой части объекта, можно построить оптико-математическую модель поляризационных тепловизионных изображений объектов любой формы.