Навигация
Модель переходных процессов в манипуляторе МРЛ-901П
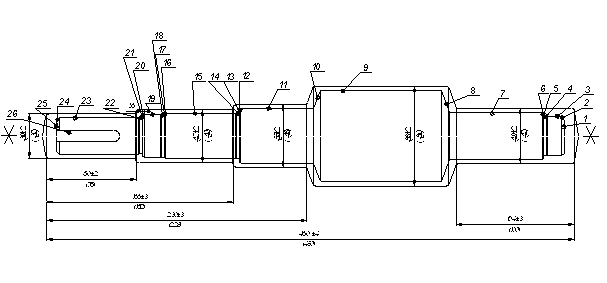
2.1 Модель переходных процессов в манипуляторе МРЛ-901П
М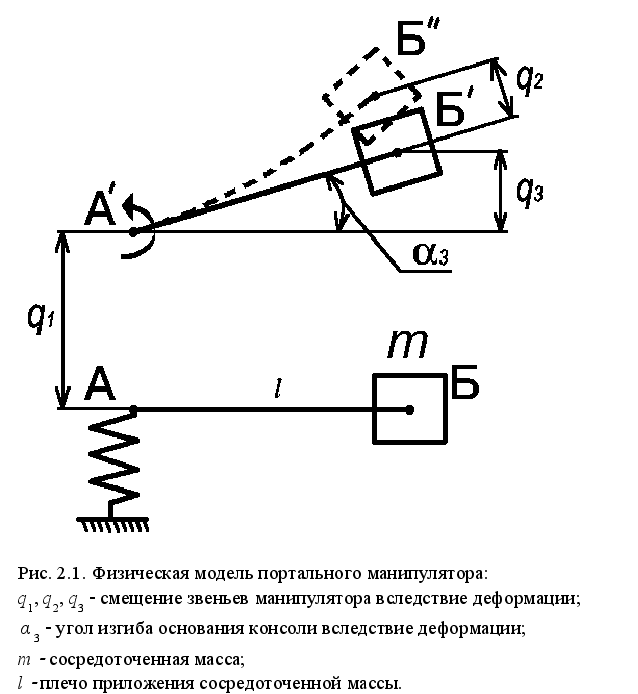
одель
портального
манипулятора
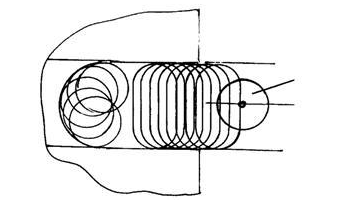
МРЛ-901П представлена
на рис. 2.1. Деформирующимися
элементами
в манипуляторе
являются: зубчатый
ремень, обозначенный
пружиной; консольная
часть, на которой
имеется сосредоточенная
масса m. Деформация
поперечной
консоли обозначена
на схеме углом
![]() .
Исходными
данными для
расчета такой
модели будут:
значение подвижной
массы m, плечо
приложения
этой массы l,
а также коэффициент
натяжения
зубчатого
ремня, определяемый
как отношение
прогиба ремня
к его длине и
влияющий на
жесткость, и
демпфирование
модуля линейного
перемещения.
.
Исходными
данными для
расчета такой
модели будут:
значение подвижной
массы m, плечо
приложения
этой массы l,
а также коэффициент
натяжения
зубчатого
ремня, определяемый
как отношение
прогиба ремня
к его длине и
влияющий на
жесткость, и
демпфирование
модуля линейного
перемещения.
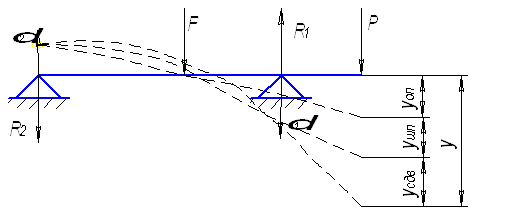
При остановке
электроприводов
подвижные массы
будут продолжать
движение под
действием
инерционных
сил, в результате
чего точки А
и Б займут положение
![]() и
и ![]() соответственно,
затем остановятся
и под действием
сил упругой
деформации
пружины и балки
начнут совершать
колебательное
движения.
соответственно,
затем остановятся
и под действием
сил упругой
деформации
пружины и балки
начнут совершать
колебательное
движения.
Рассматриваемая
модель имеет
три степени
свободы, обозначим
независимые
обобщенные
координаты
как ![]() ,
,
![]() и
и ![]() .
Для описания
данной модели
воспользуемся
уравнением
Лагранжа второго
рода:
.
Для описания
данной модели
воспользуемся
уравнением
Лагранжа второго
рода:
|
| (2.1) |
где T кинетическая энергия системы; Q обобщенная сила; k количество степеней свободы.
Кинетическая энергия системы с тремя степенями свободы является однородной квадратичной формой обобщенных скоростей [5]:
|
| (2.2) |
Коэффициенты
![]() являются
функциями
координат
являются
функциями
координат ![]() ,
,
![]() и
и ![]() .
.
Предположим,
что обобщенные
координаты
отсчитываются
от положения
равновесия,
где ![]() .
.
Располагая
коэффициенты
![]() по степеням
и пологая для
упрощения
записи
по степеням
и пологая для
упрощения
записи ![]() ,
получим:
,
получим:
|
| (2.3) |
Потенциальная
энергия ![]() системы:
системы:
|
| (2.4) |
При этом учитываем,
что в положении
равновесия
![]() обобщенные
силы также
обращаются
в нуль.
обобщенные
силы также
обращаются
в нуль.
В (2.4) для упрощения приняты следующие обозначения:
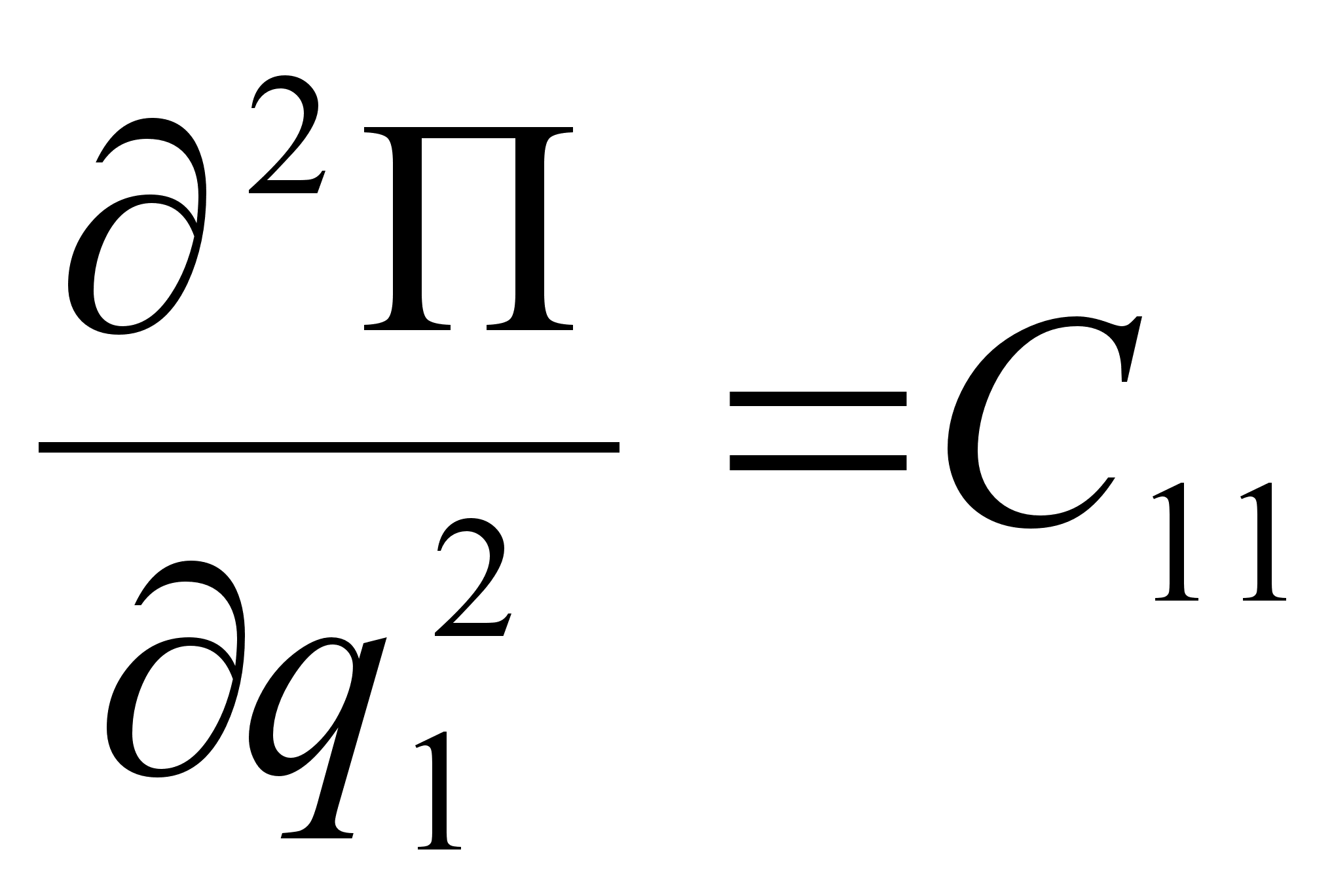 ,
,
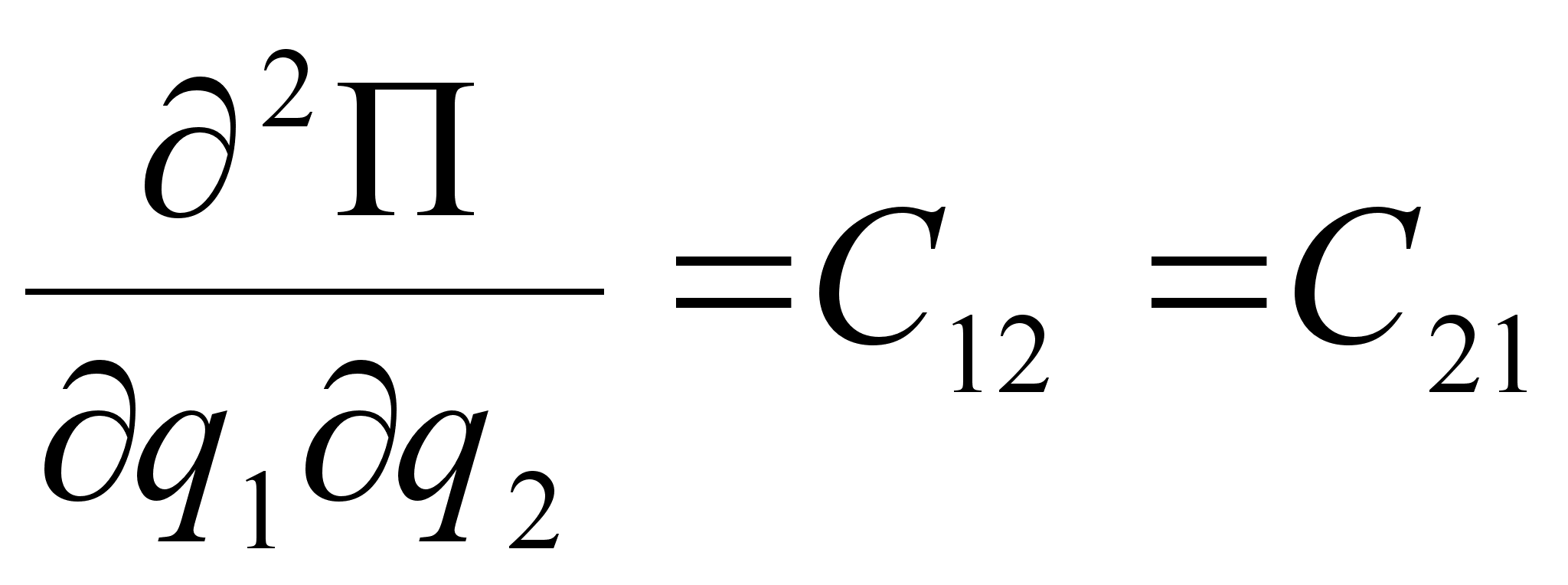 ,
,
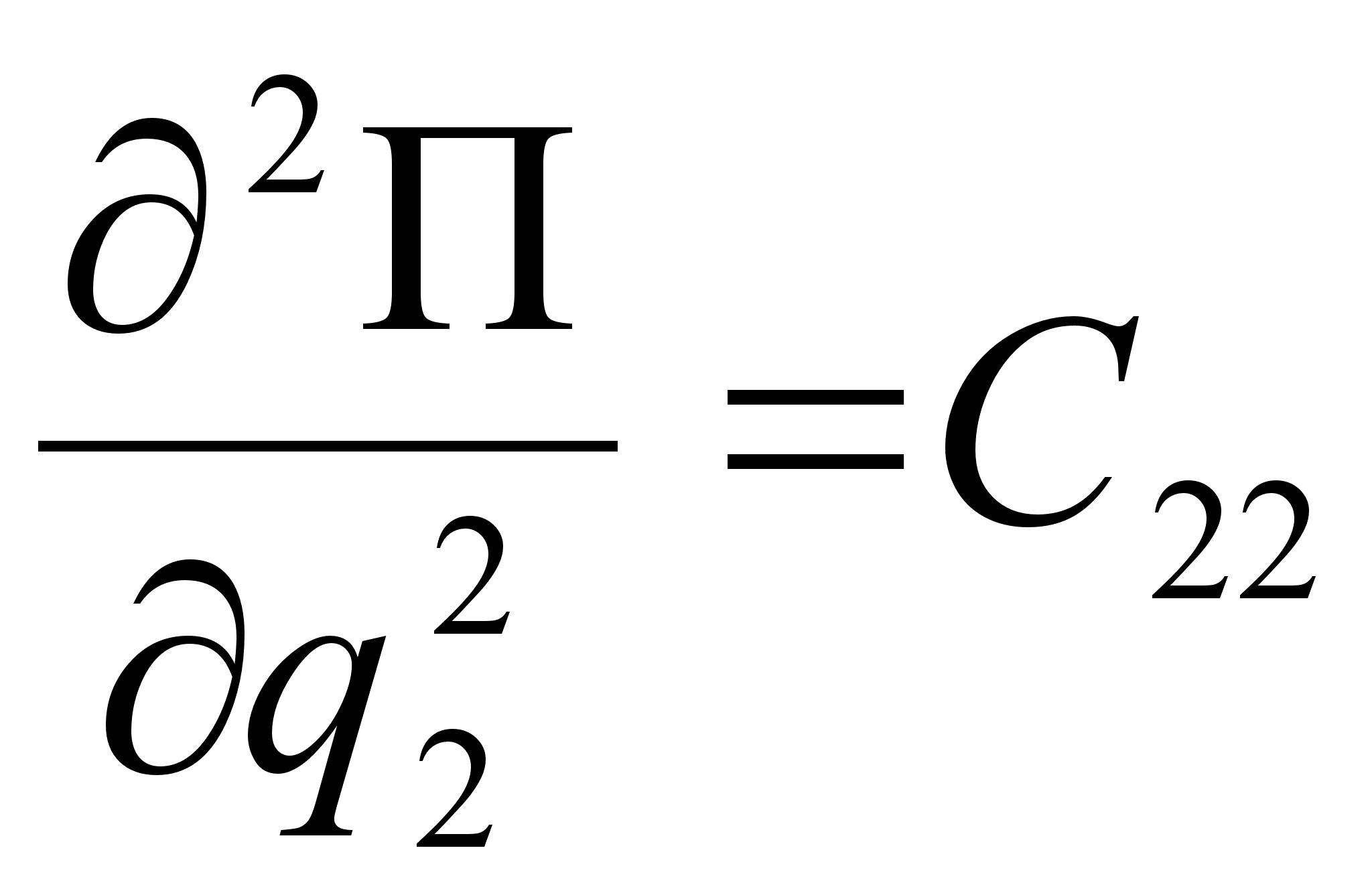 ,
,
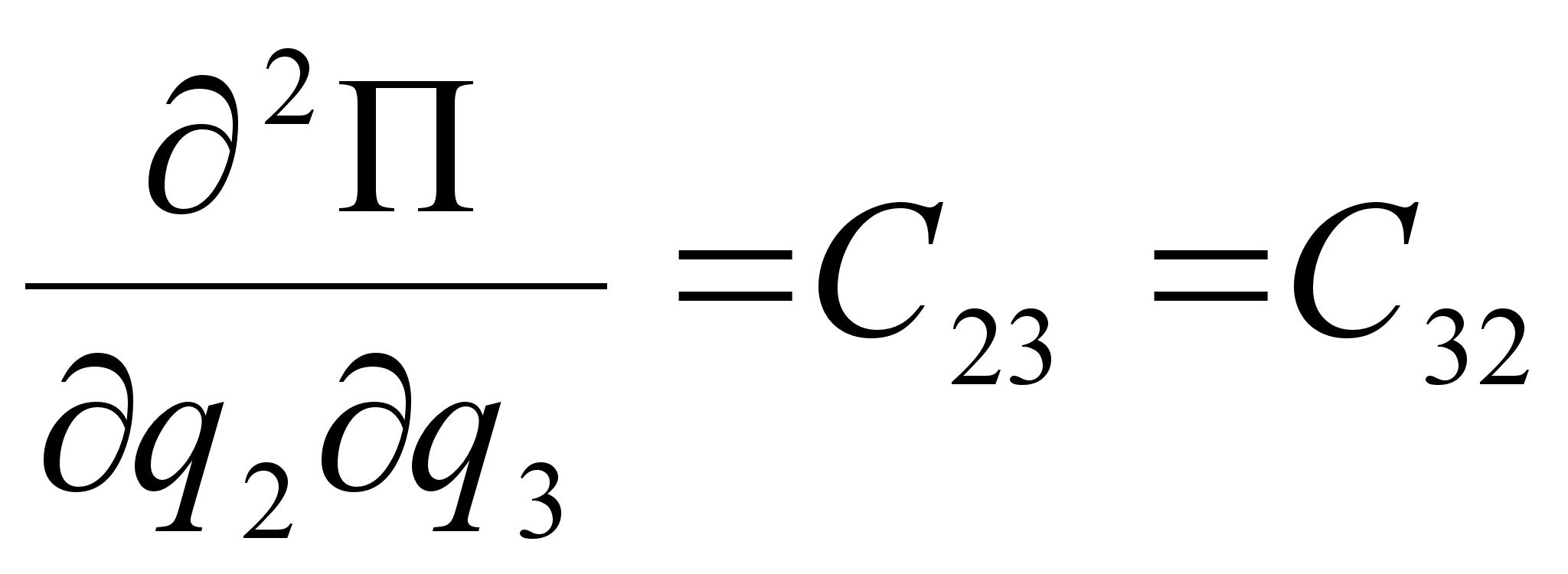 ,
,
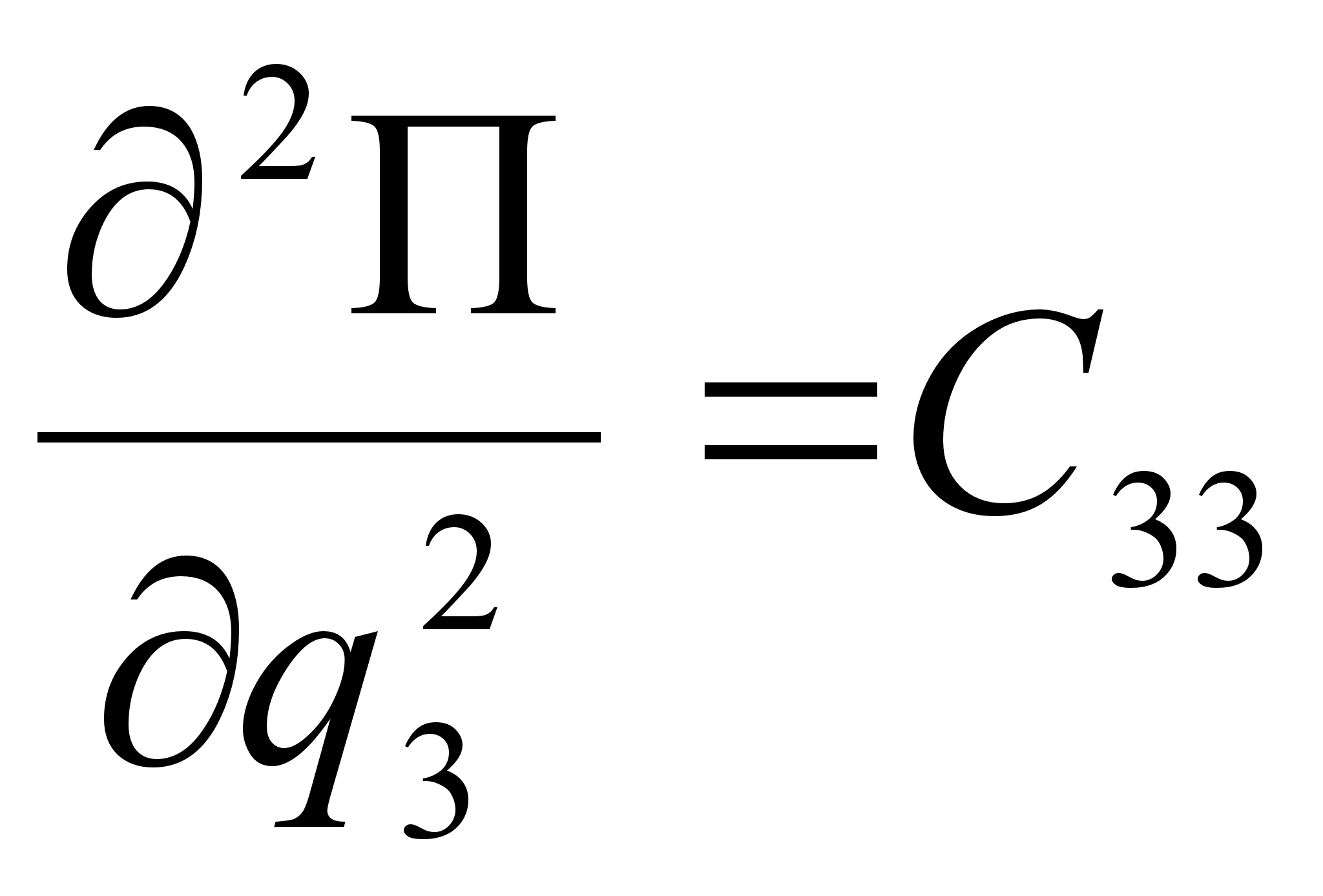 ,
,
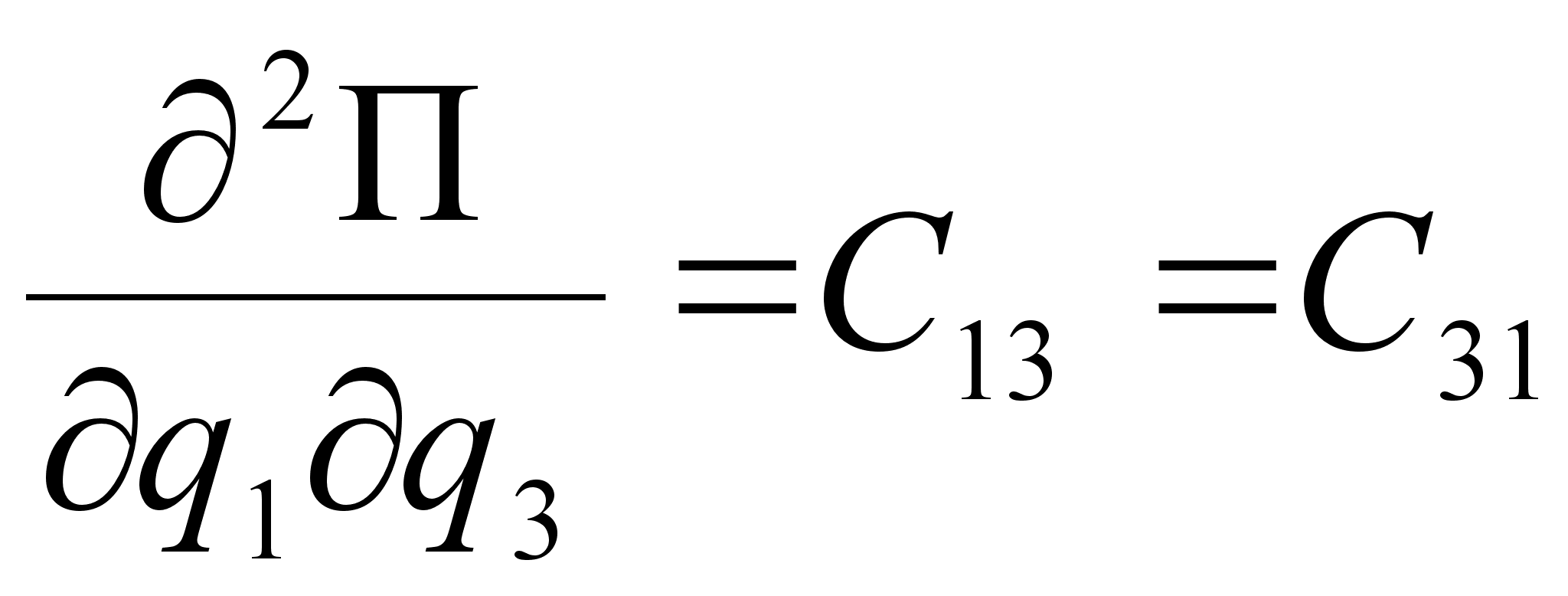 .
.
Для составления
дифференциальных
уравнений
свободных
колебаний в
форме уравнений
Лагранжа второго
рода, выразим
потенциальную
энергию через
обобщенные
координаты.
Рассмотрим
равновесие
системы, на
которую действуют
силы ![]()
![]() …,
…,![]() .
Потенциальная
энергия в состоянии
устойчивого
равновесия
имеет минимум,
равный нулю,
а при вызванном
действием сил
.
Потенциальная
энергия в состоянии
устойчивого
равновесия
имеет минимум,
равный нулю,
а при вызванном
действием сил
![]() отклонении
от него выражается
квадратичной
формой вида
(2.4).
отклонении
от него выражается
квадратичной
формой вида
(2.4).
Элементарная работа всех сил действующих на систему, по принципу возможных перемещений должна быть равна нулю:
|
| (2.5) |
Замечая, что
| |
а также приравнивая
к нулю коэффициенты
при независимых
вариациях ![]() ,
,
![]() и
и ![]() ,
получаем три
уравнения:
,
получаем три
уравнения:
|
| (2.6) |
Здесь ![]() ,
,
![]() и
и ![]() обобщенные
силы для системы
сил
обобщенные
силы для системы
сил ![]()
![]() …,
…,![]() ,
уравновешивающих
потенциальные
силы, возникающие
при отклонении
системы из
положения
равновесия
,
уравновешивающих
потенциальные
силы, возникающие
при отклонении
системы из
положения
равновесия
![]() .
Заменяя в (2.6)
производные
потенциальной
энергии их
выражениями
согласно (2.4),
получим систему
уравнений,
определяющих
значение координат
.
Заменяя в (2.6)
производные
потенциальной
энергии их
выражениями
согласно (2.4),
получим систему
уравнений,
определяющих
значение координат
![]() ,
,
![]() и
и ![]() в положении
равновесия:
в положении
равновесия:
|
| (2.7) |
причем ![]() ,
,
![]() и
и ![]() .
.
Решение системы (2.7) имеет вид:
|
| (2.8) |
где
|
| (2.9) |
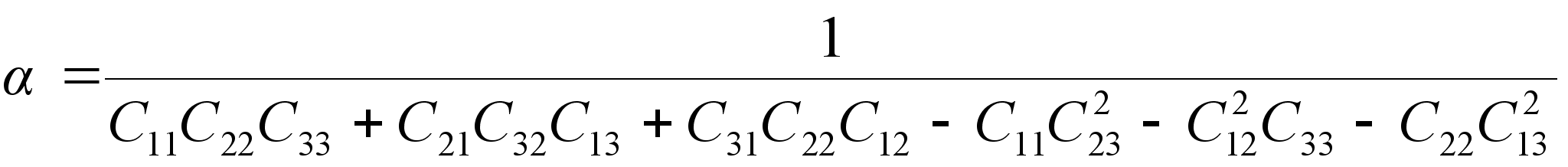 .
.
На систему
действуют
обобщенные
силы, которыми
являются инерционные
силы и силы
сопротивления
движению. Обычно
в сложных системах
в целях упрощения
[4, 5]
силу сопротивления
принимают
пропорциональной
первой степени
скорости движения.
С целью упрощения
условимся, что
угол ![]() мал и координаты
массы m можно
записать как
мал и координаты
массы m можно
записать как
![]() .
Поэтому на
основании
кинетостатики
можем записать:
.
Поэтому на
основании
кинетостатики
можем записать:
|
| (2.10) |
где ![]()
обобщенная
сила,
обобщенная
сила, ![]() коэффициент
сопротивления
пропорциональный
первой степени
скорости движения
массы m. Так
как масса собственно
консоли манипулятора
МРЛ-901П меньше
массы закрепленных
на ней рабочих
головок, захватов
и деталей, для
упрощения
примем условие,
что точка
исследования
колебаний
(практически
рабочий
орган манипулятора)
совпадает с
точкой приложения
сосредоточенной
массы m.
коэффициент
сопротивления
пропорциональный
первой степени
скорости движения
массы m. Так
как масса собственно
консоли манипулятора
МРЛ-901П меньше
массы закрепленных
на ней рабочих
головок, захватов
и деталей, для
упрощения
примем условие,
что точка
исследования
колебаний
(практически
рабочий
орган манипулятора)
совпадает с
точкой приложения
сосредоточенной
массы m.
Сила ![]() действует на
все звенья
манипулятора следовательно:
действует на
все звенья
манипулятора следовательно:
| | (2.11) |
Коэффициенты
![]() в
(2.7) будем определять
из того, что
согласно (2.11)
звенья можно
рассматривать
независимо
друг от друга.
Положим сначала,
что
в
(2.7) будем определять
из того, что
согласно (2.11)
звенья можно
рассматривать
независимо
друг от друга.
Положим сначала,
что
![]() действует
только по координате
действует
только по координате
![]() ,
затем только
по координате
,
затем только
по координате
![]() и наконец только
по координате
и наконец только
по координате
![]() ,
тогда в выражение
(2.7) можно переписать:
,
тогда в выражение
(2.7) можно переписать:
| | (2.12) |
таким образом
![]() ,
используя (2.9)
находим:
,
используя (2.9)
находим:
| | (2.13) |
Коэффициенты
![]() ,
,
![]() и
и ![]() определяют
податливость
звеньев манипулятора
по координатам
определяют
податливость
звеньев манипулятора
по координатам
![]() ,
,
![]() и
и ![]() соответственно.
Выражая податливость
звеньев через
их жесткость,
запишем:
соответственно.
Выражая податливость
звеньев через
их жесткость,
запишем:
|
| (2.14) |
где ![]() ,
,
![]() и
и ![]() жесткости
звеньев по
координатам
жесткости
звеньев по
координатам
![]() ,
,
![]() и
и ![]() соответственно.
соответственно.
Подставляя (2.14) , (2.11) и (2.10) в (2.8) получим:
|
| (2.15) |
Для решения этой системы нужно выразить скорость и ускорение массы m через их составляющие:
|
| (2.16) |
Поскольку в
манипуляторе
суммарную
жесткость
удобно экспериментально
определять,
прикладывая
соответствующее
усилие к
его рабочему
органу, и так
как в конечном
итоге необходимо
определить
положение массы
m, координаты
которой выражаются
как ![]() ,
то для этого
достаточно
сложить уравнения
в выражении
(2.15):
,
то для этого
достаточно
сложить уравнения
в выражении
(2.15):
|
| (2.17) |
или:
|
| (2.18) |
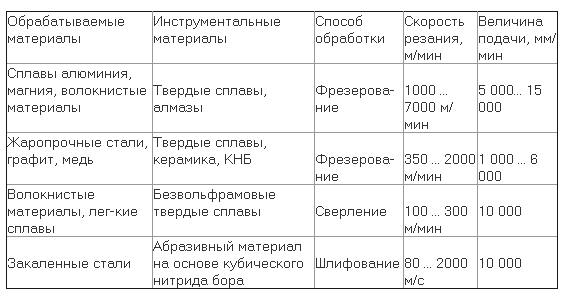
где С суммарная жесткость звеньев манипулятора.
Анализ показывает, что величина C является переменной и зависит от плеча приложения l сосредоточенной массы m.
Преобразуя (2.18), получаем уравнение описывающие переходный процесс в системе:
|
| (2.19) |
Уравнение (2.19) легко решается классическим способом при следующих начальных условиях:
| | (2.20) |
где ![]() скорость
рабочего органа
манипулятора
в момент выхода
на конечную
точку.
скорость
рабочего органа
манипулятора
в момент выхода
на конечную
точку.
Выражение (2.19) представляет собой линейное дифференциальное уравнение второго порядка. Будем искать частное решение уравнения в виде:
| | (2.21) |
где ![]() и
и ![]() произвольные
постоянные,
которые могут
быть определены
из начальных
условий: при
t = 0;
произвольные
постоянные,
которые могут
быть определены
из начальных
условий: при
t = 0; ![]() и
и ![]() корни
характеристического
уравнения:
корни
характеристического
уравнения:
| | (2.22) |
Решение уравнения (2.22) будет иметь вид:
| | (2.23) |
Определим
произвольные
постоянные
![]() и
и ![]() ,
решая систему
уравнений:
,
решая систему
уравнений:
| | (2.24) |
Решение системы (2.24) будет иметь вид:
| | (2.25) |
если учесть (2.20) то:
| | (2.26) |
подставляя (2.26) в (2.21) и с учетом (2.23) имеем:
| | (2.27) |
где ![]() реальная
часть;
реальная
часть; 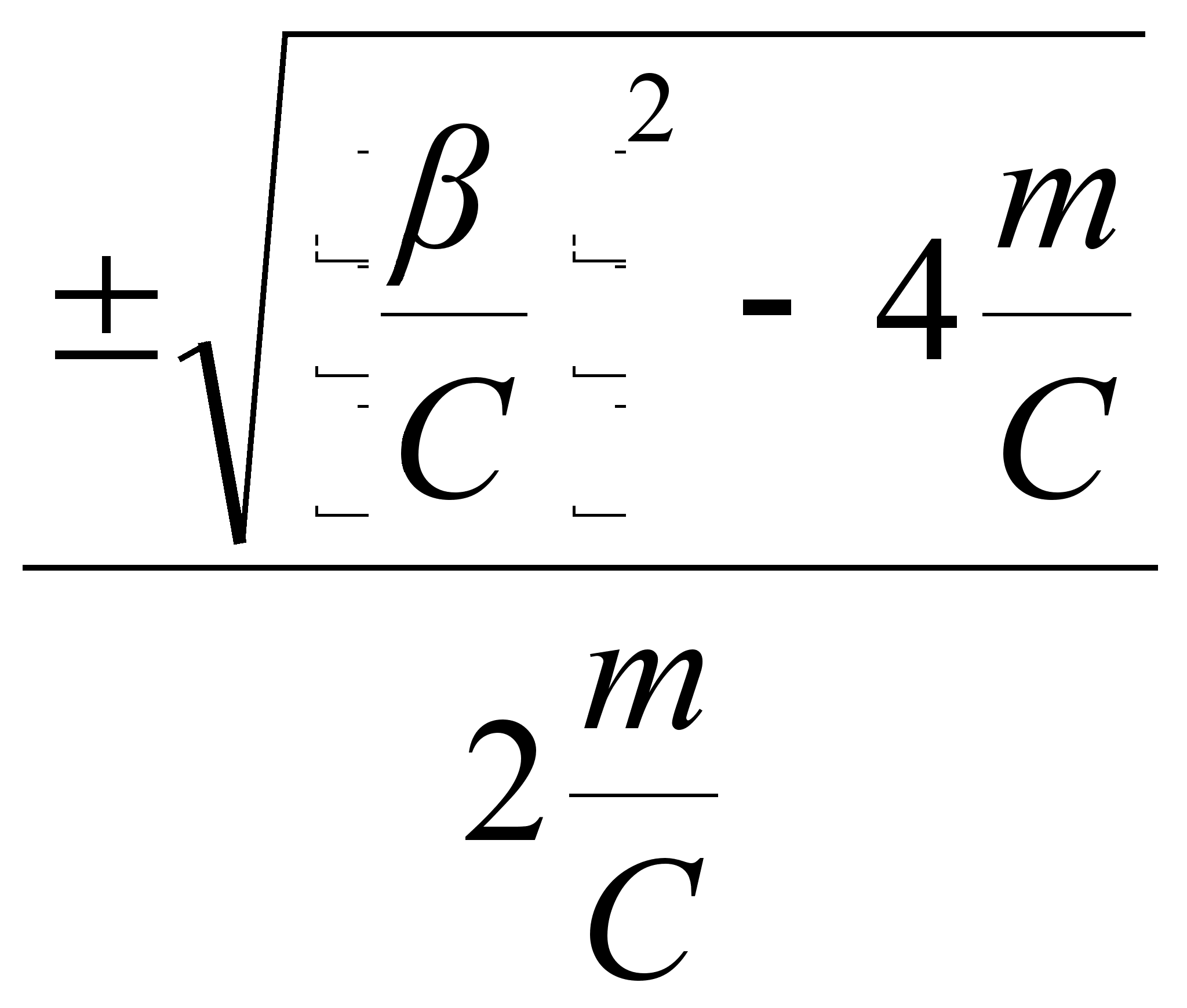 мнимая
часть.
мнимая
часть.
Тогда разделяя реальную и мнимую части в (2.27) получим:
| | (2.28) |
Учитывая что:
|
| (2.29) |
имеем:
|
| (2.30) |
Преобразуя (2.30) получим решение уравнения (2.19):
| | (2.31) |
Прологарифмируем выражение (2.31) предварительно подставив в него значение допустимой погрешности позиционирования:
| | (2.32) |
где ![]() допустимая
погрешность
позиционирования.
допустимая
погрешность
позиционирования.
Преобразуя (2.32) получим выражение для определения времени переходного процесса:
| | (2.33) |
Для расчета
жесткости C
и коэффициента
демпфирования
![]() в модели используются
экспериментально
полученные
зависимости.
В частности
коэффициент
демпфирования
определяется
по осциллограмме
затухания
колебаний
рабочего органа.
в модели используются
экспериментально
полученные
зависимости.
В частности
коэффициент
демпфирования
определяется
по осциллограмме
затухания
колебаний
рабочего органа.
Таким образом, время переходного процесса, для данного типа манипулятора при заданной массе положении рабочего органа определяется по выражению (2.33), в котором коэффициенты жесткости и демпфирования предварительно определены экспериментально.
Похожие работы
... уменьшение времени перемещения, что можно использовать на операциях с низким требованием к точности, хотя это уменьшение весьма не значительное. 4. Программные средства для исследования динамической модели портального манипулятора 4.1 Программа для вычисления параметров переходного процесса портального манипулятора Для исследования полученной динамической модели, построения графиков приведенных в ...
... рабочей позиции, фиксацию устройства или спутника на рабочей позиции оформляются в виде таблицы 3.1. В данной работе предлагается разработка автоматической линии для осуществления той части техпроцесса, которая связана со сверлильной и фрезерной обработкой поверхностей и отверстий. Таким образом, проектируемая линия должна обеспечивать указанную в задании производительность. Для этого произведем ...
... за две-три недели. Во время обследований необходимо избегать нарушений в работе других видов транспорта четкой координацией управления ими. Изучение пассажиропотоков позволяет выявить основные закономерности их колебания для использования результатов обследований в планировании и организации перевозок. Иначе говоря, характер изменения пассажиропотоков на маршрутах и в целом по конкретному ...
... системой ЧПУ и обеспечивает надежную работу также в условиях безлюдного производства. При этом предотвращаются повреждения шпинделя и тем самым ненужные дорогостоящие простои. высокоскоростной механический обработка инструмент шпиндель Рис. 2. Порядок точности – единицы μ обеспечивается датчиком (1) для измерения аксиального смещения вала шпинделя; 2 – датчик измерения температуры. 3. ...
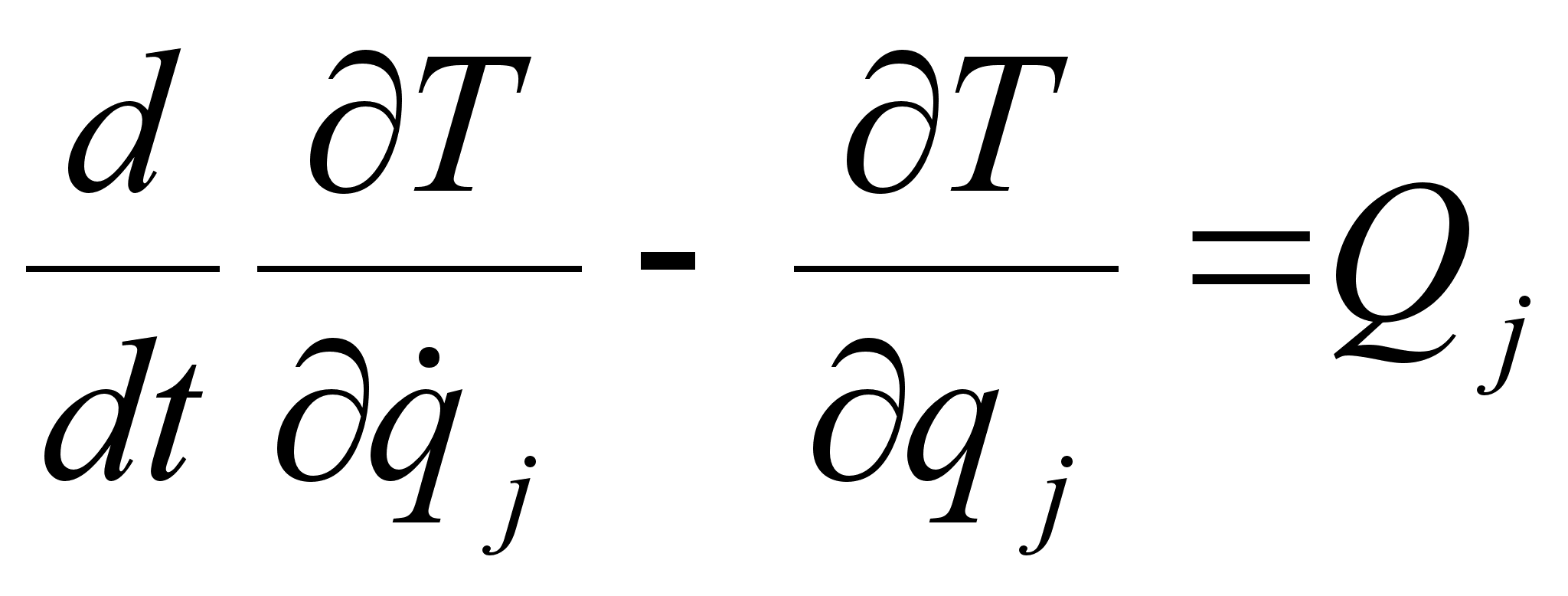 (j = 1,2,…,k),
(j = 1,2,…,k),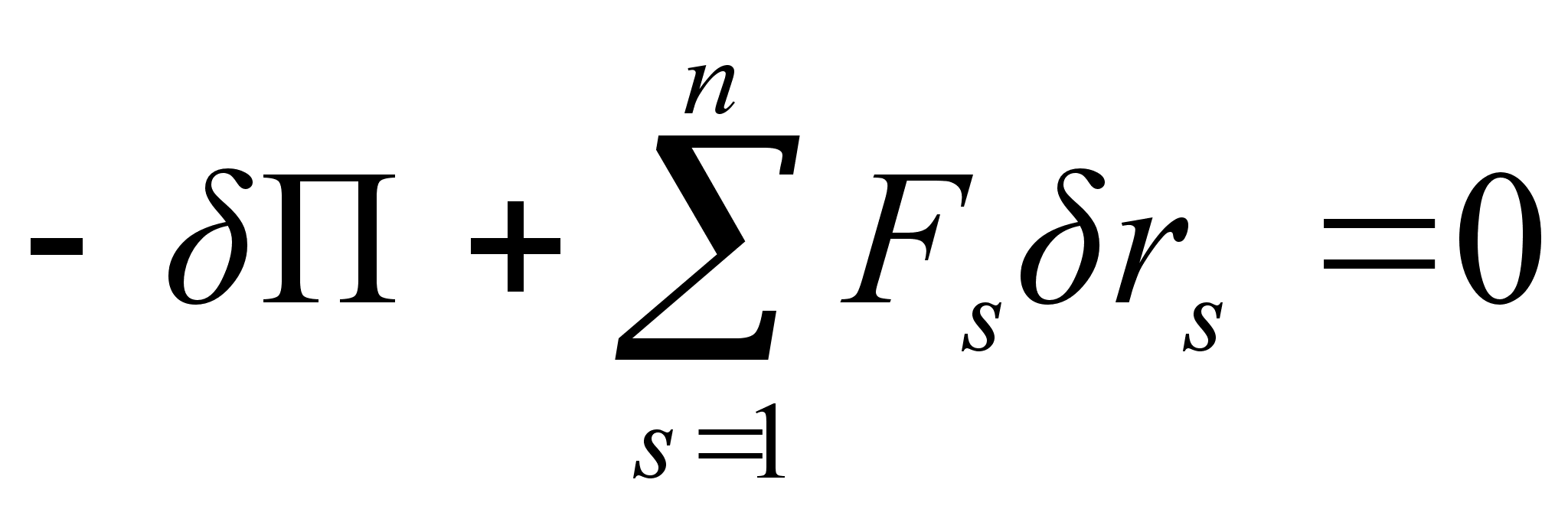 .
.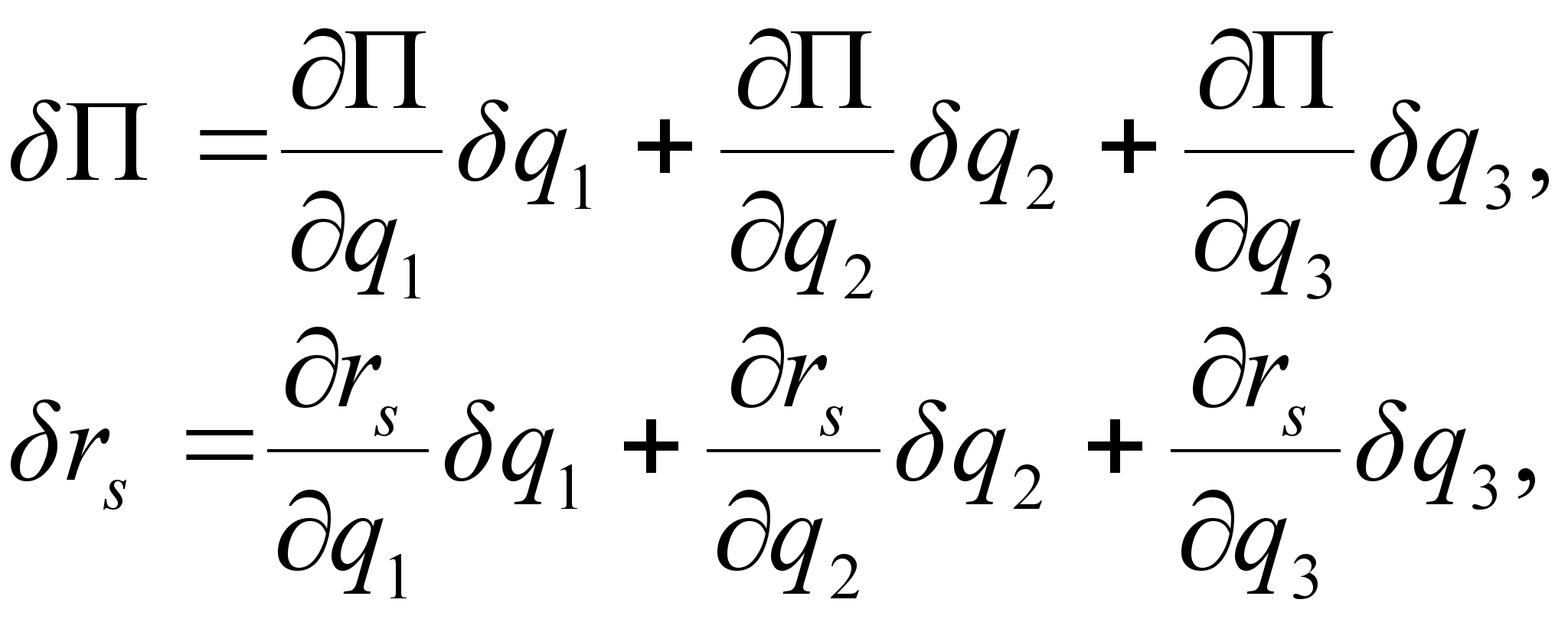
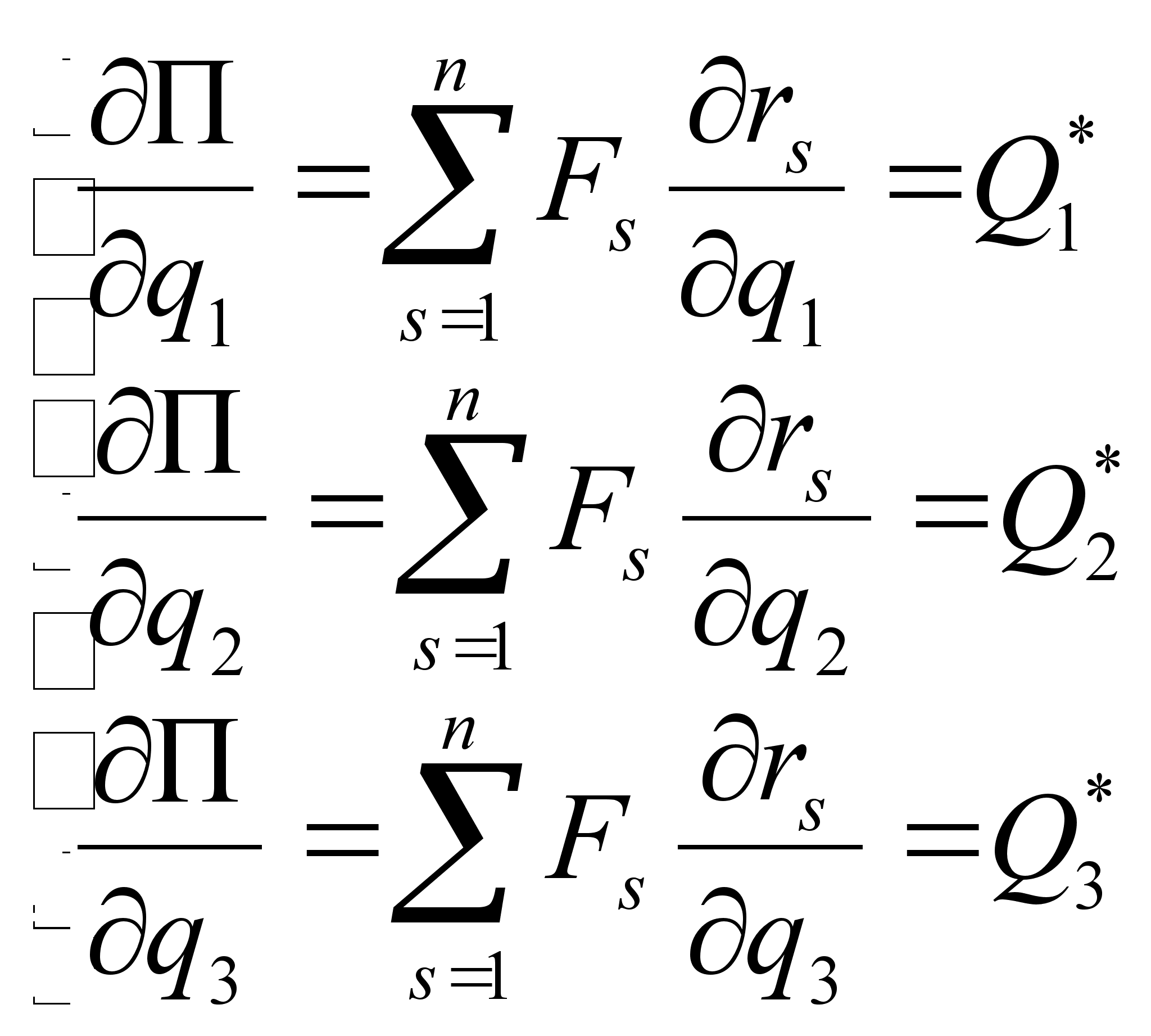 ,
,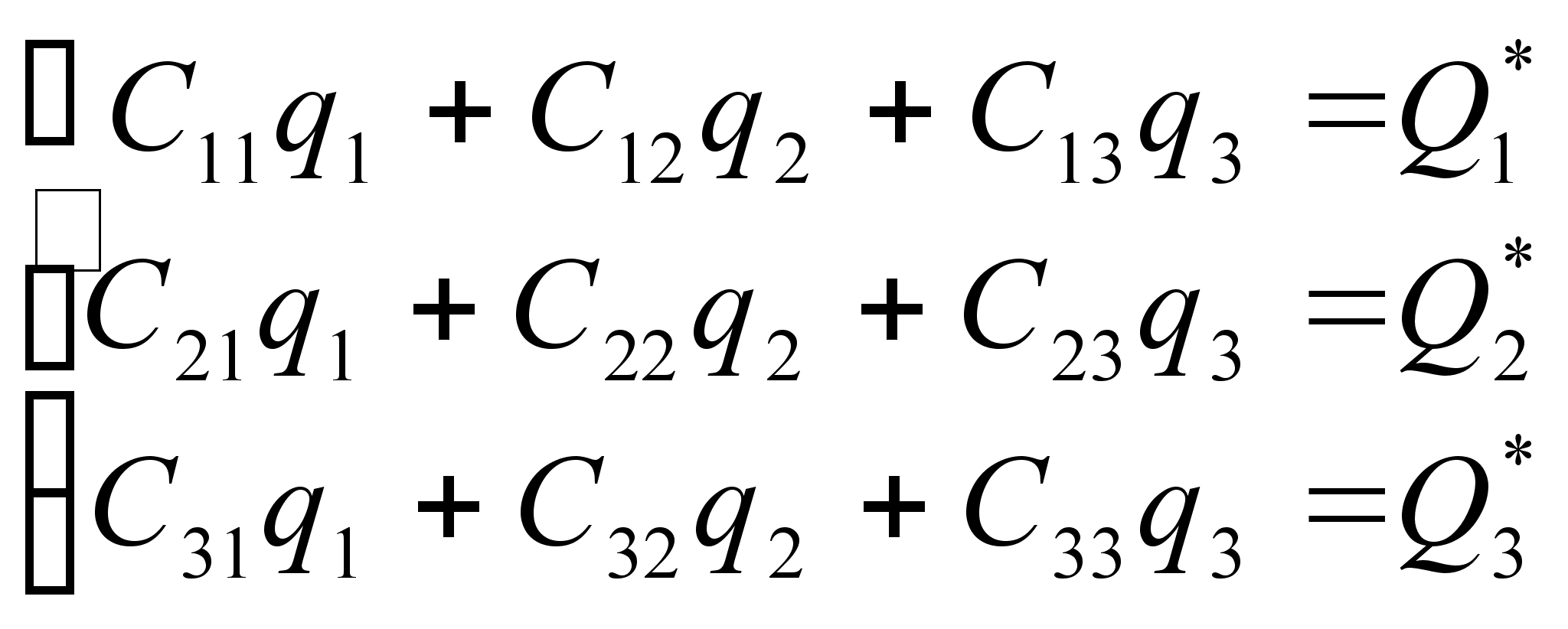 ,
,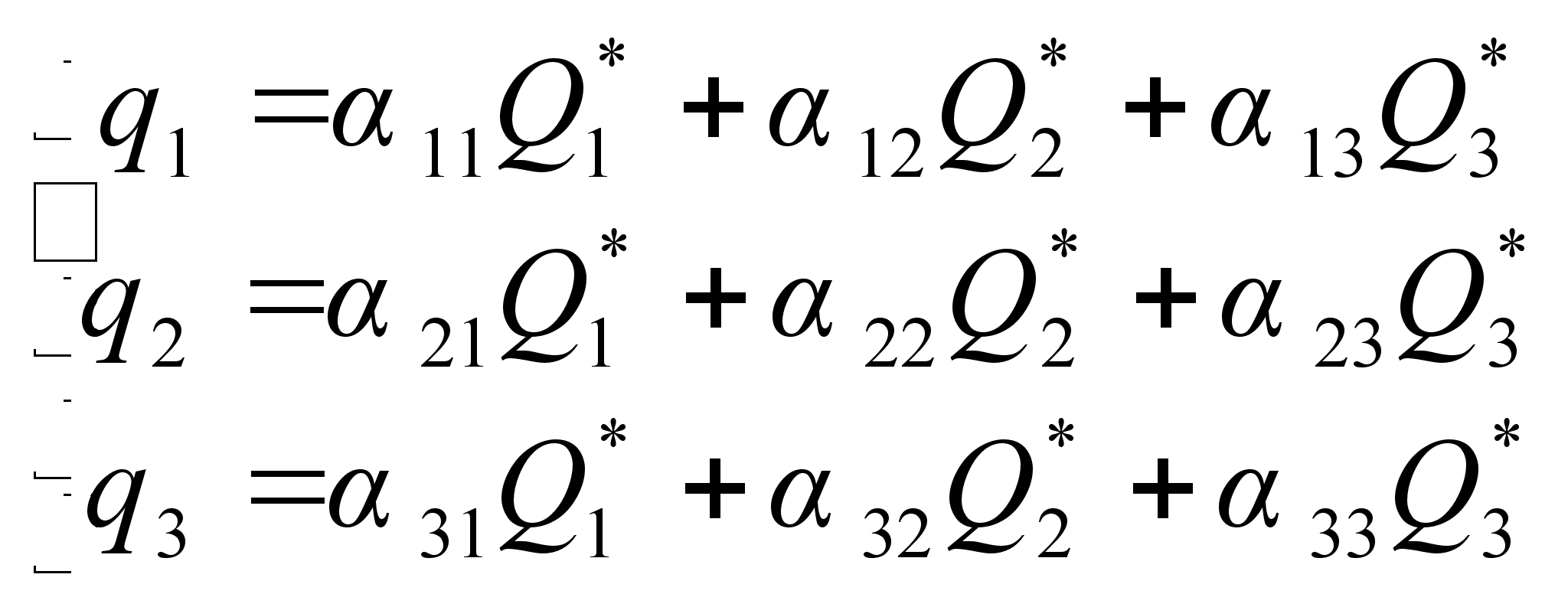 ,
,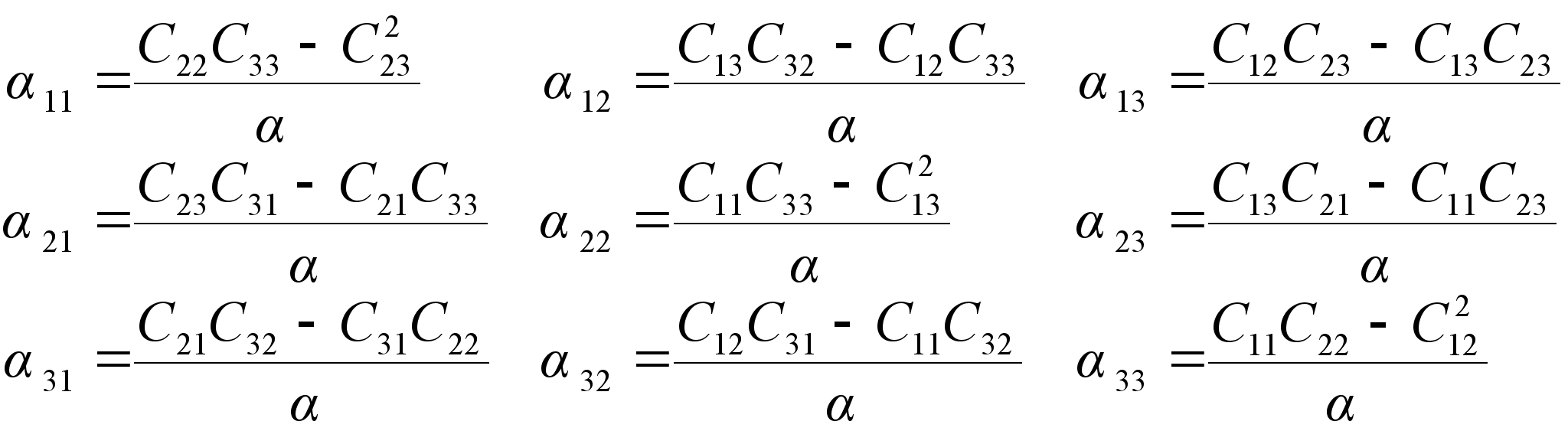
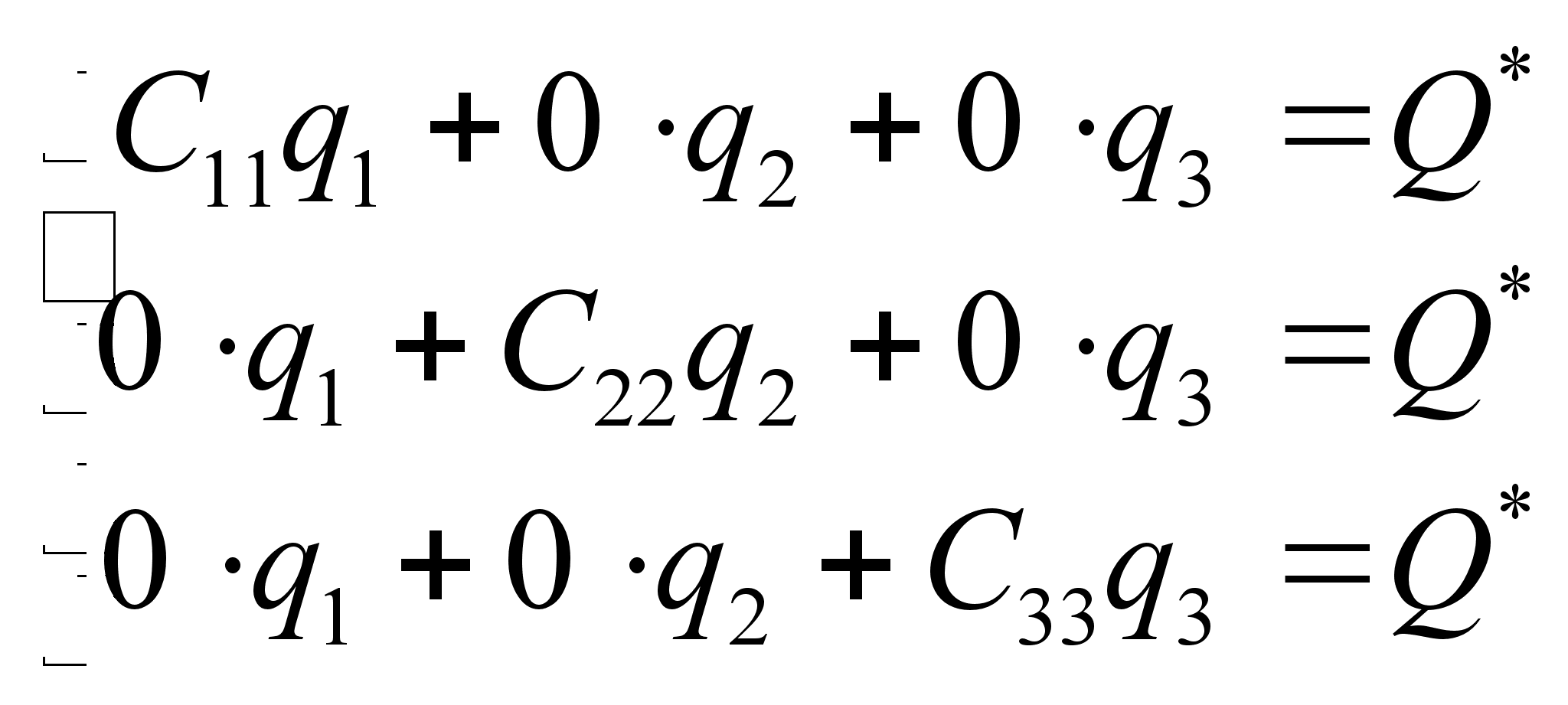 ,
,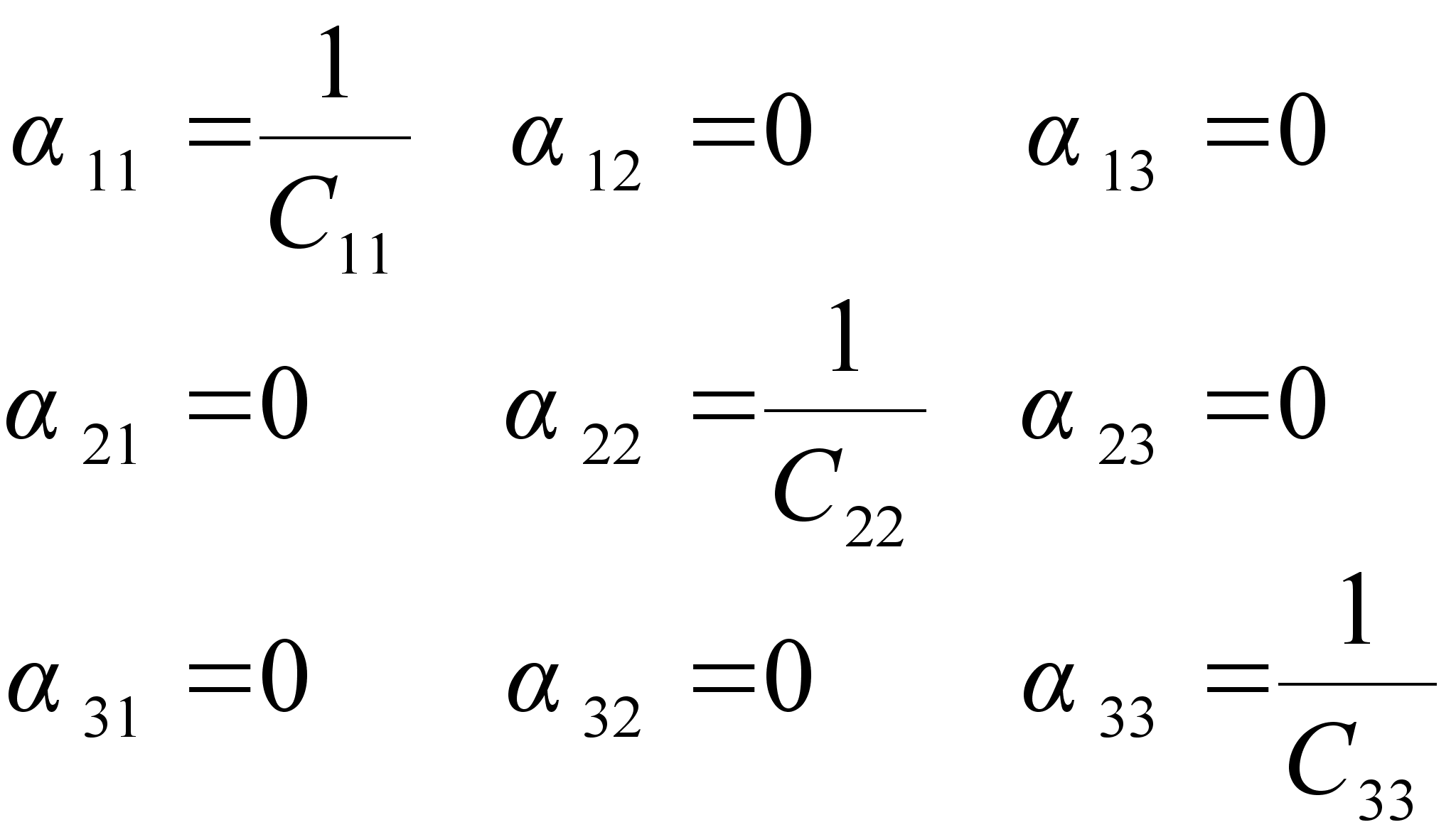
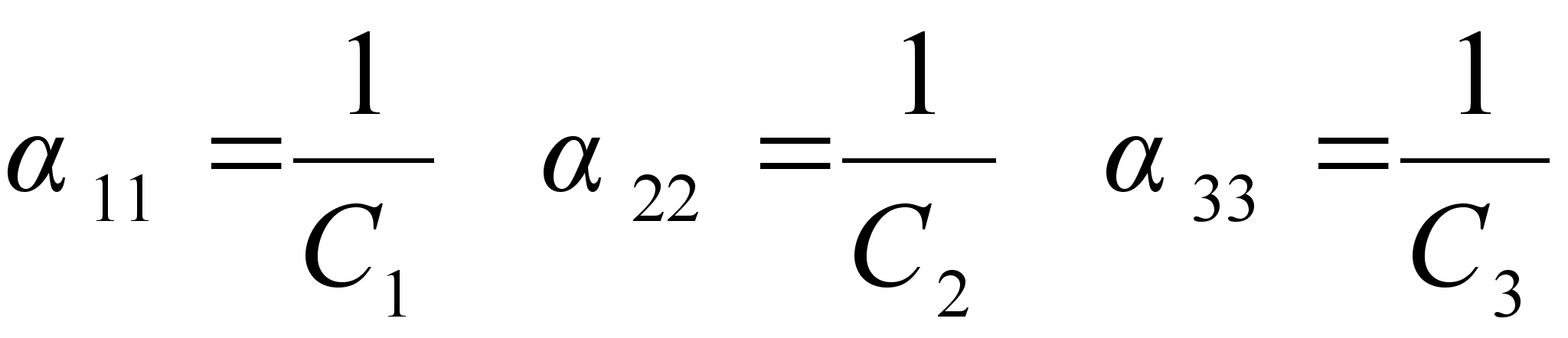 ,
,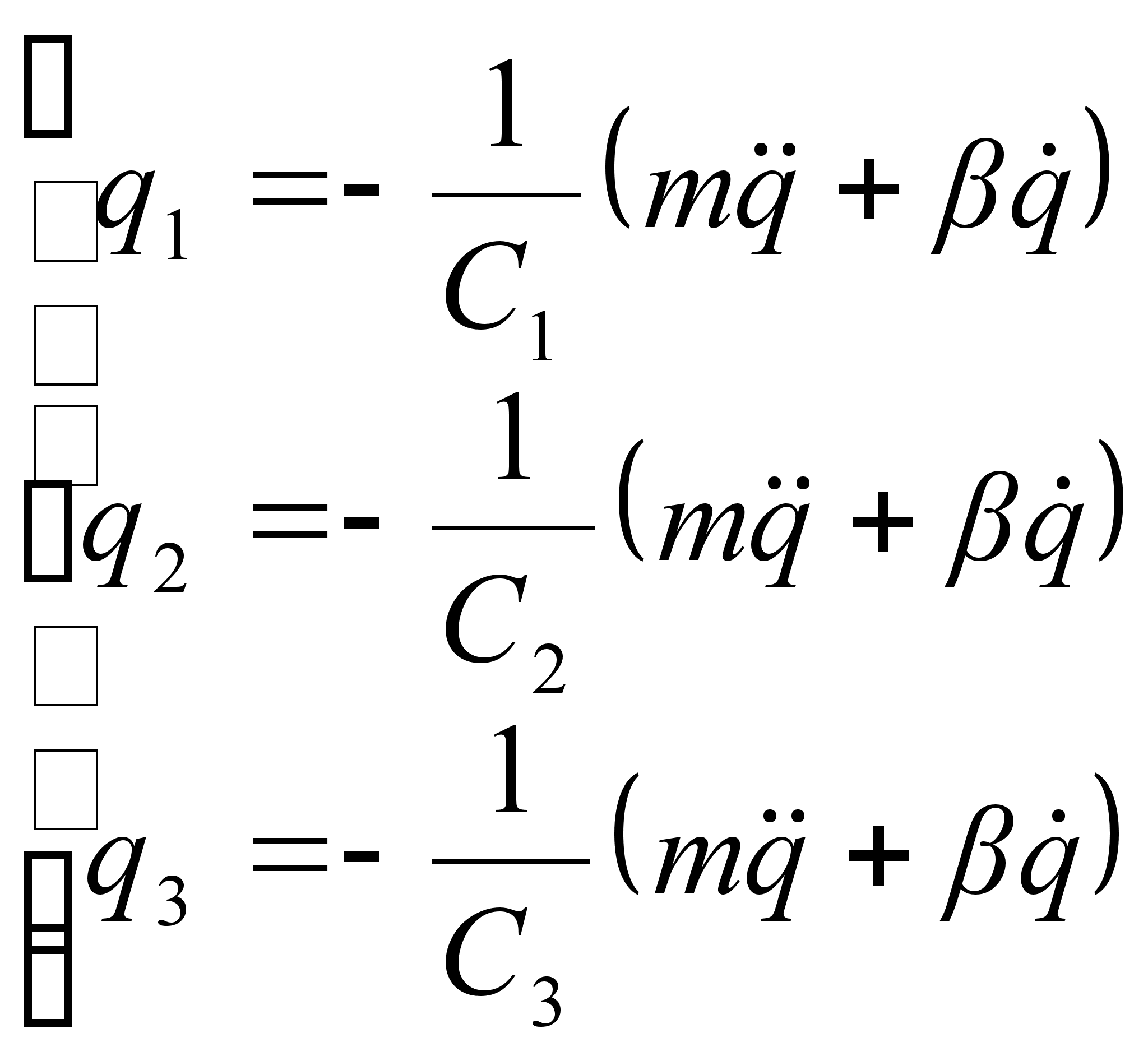
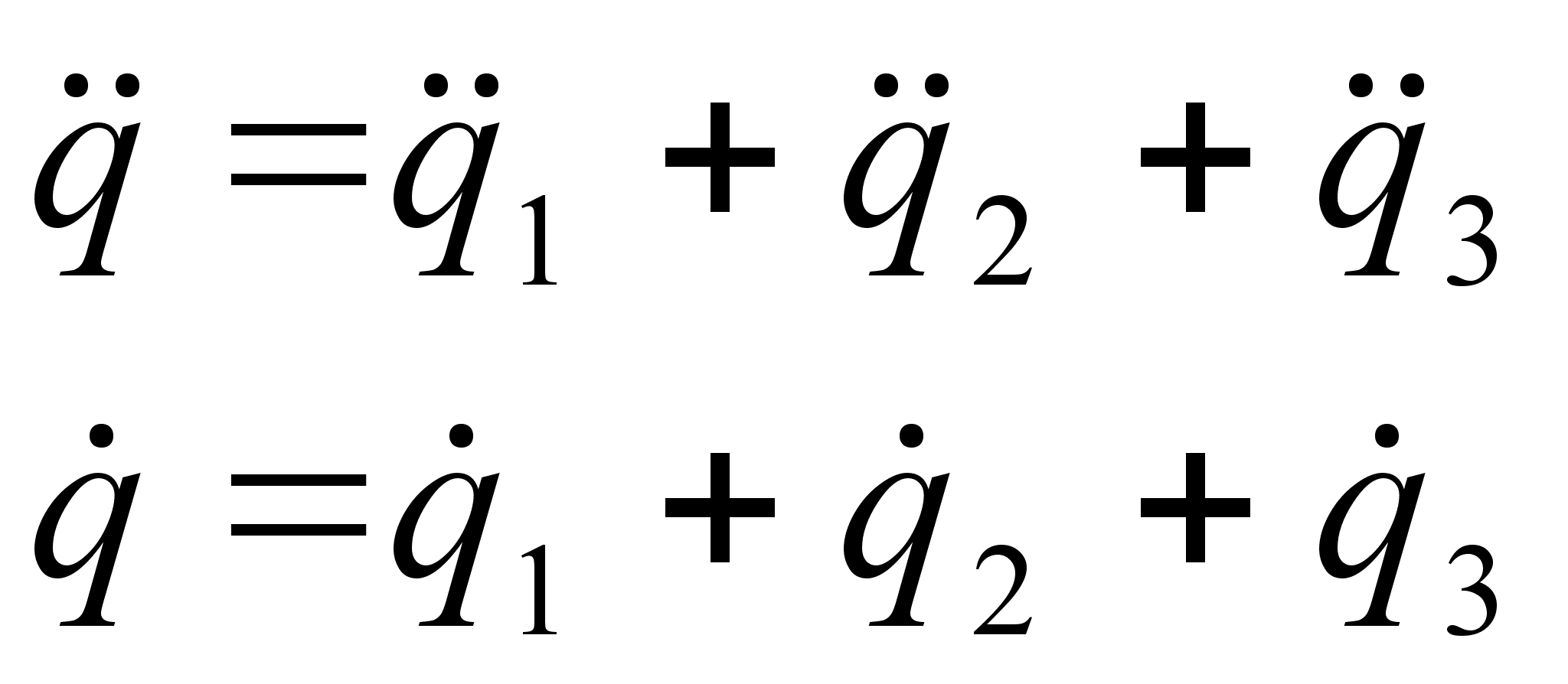 .
.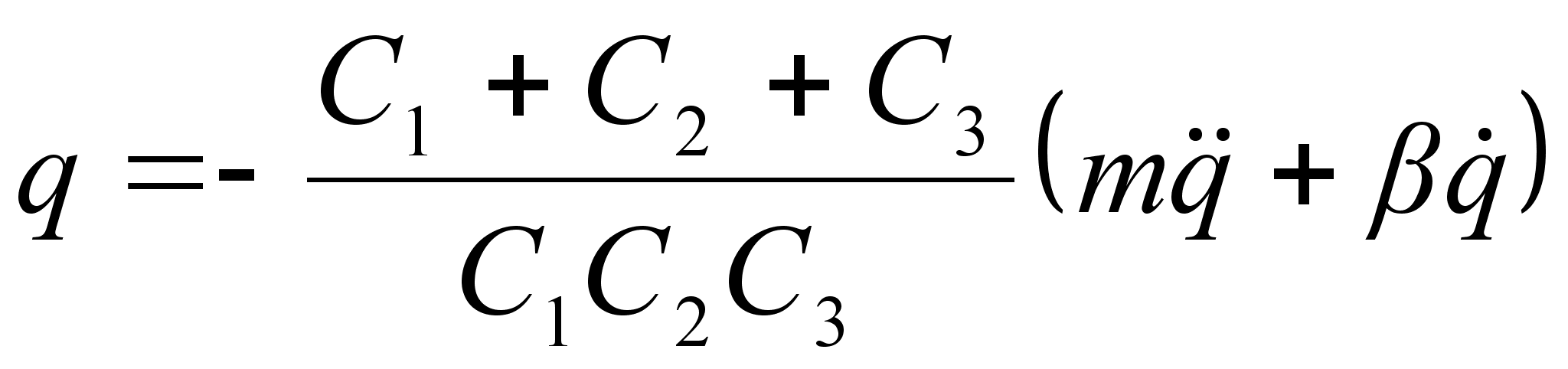
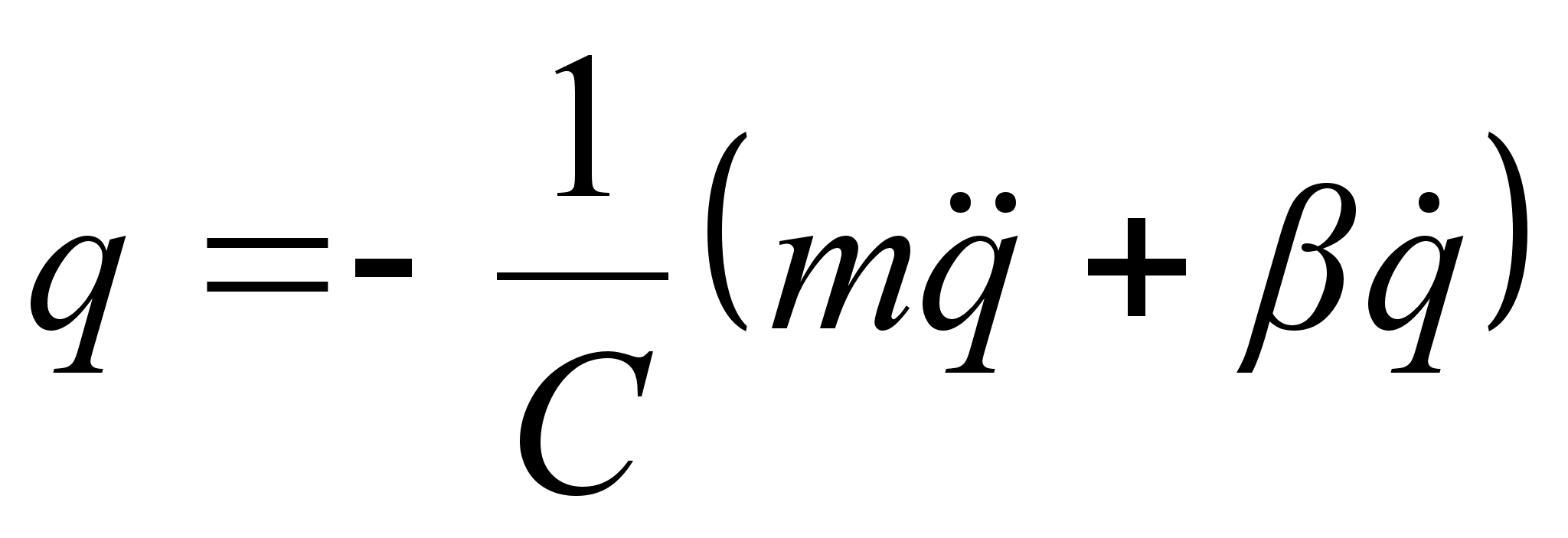 ,
,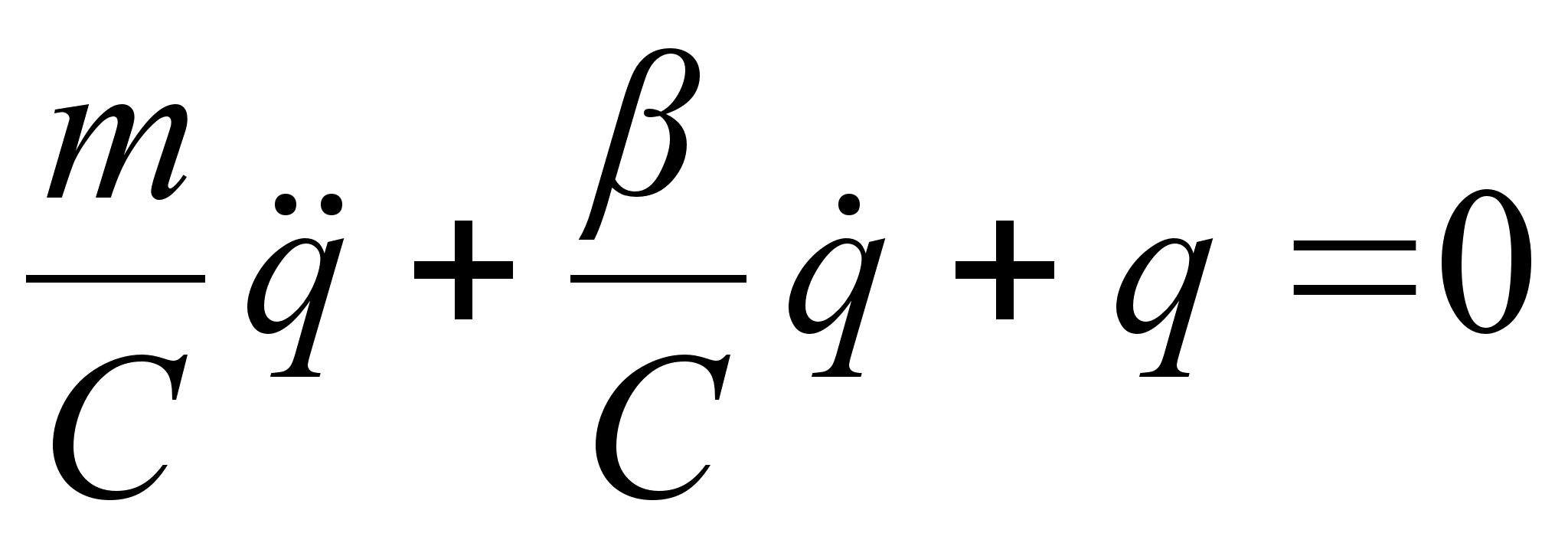 .
.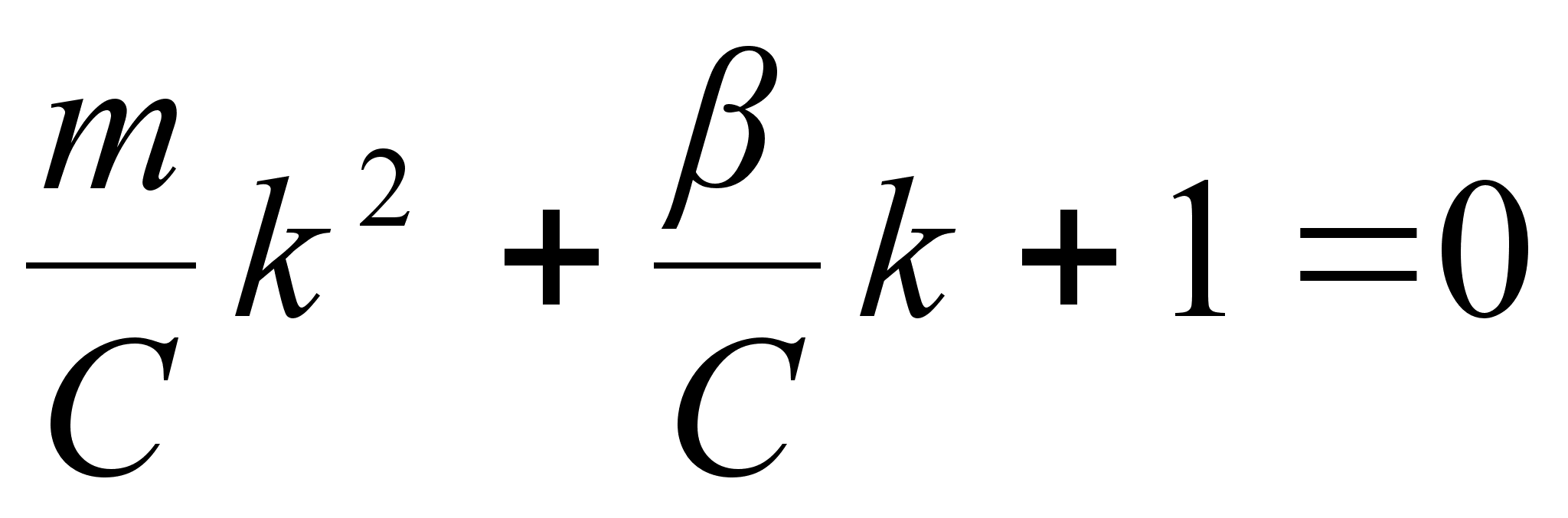 .
.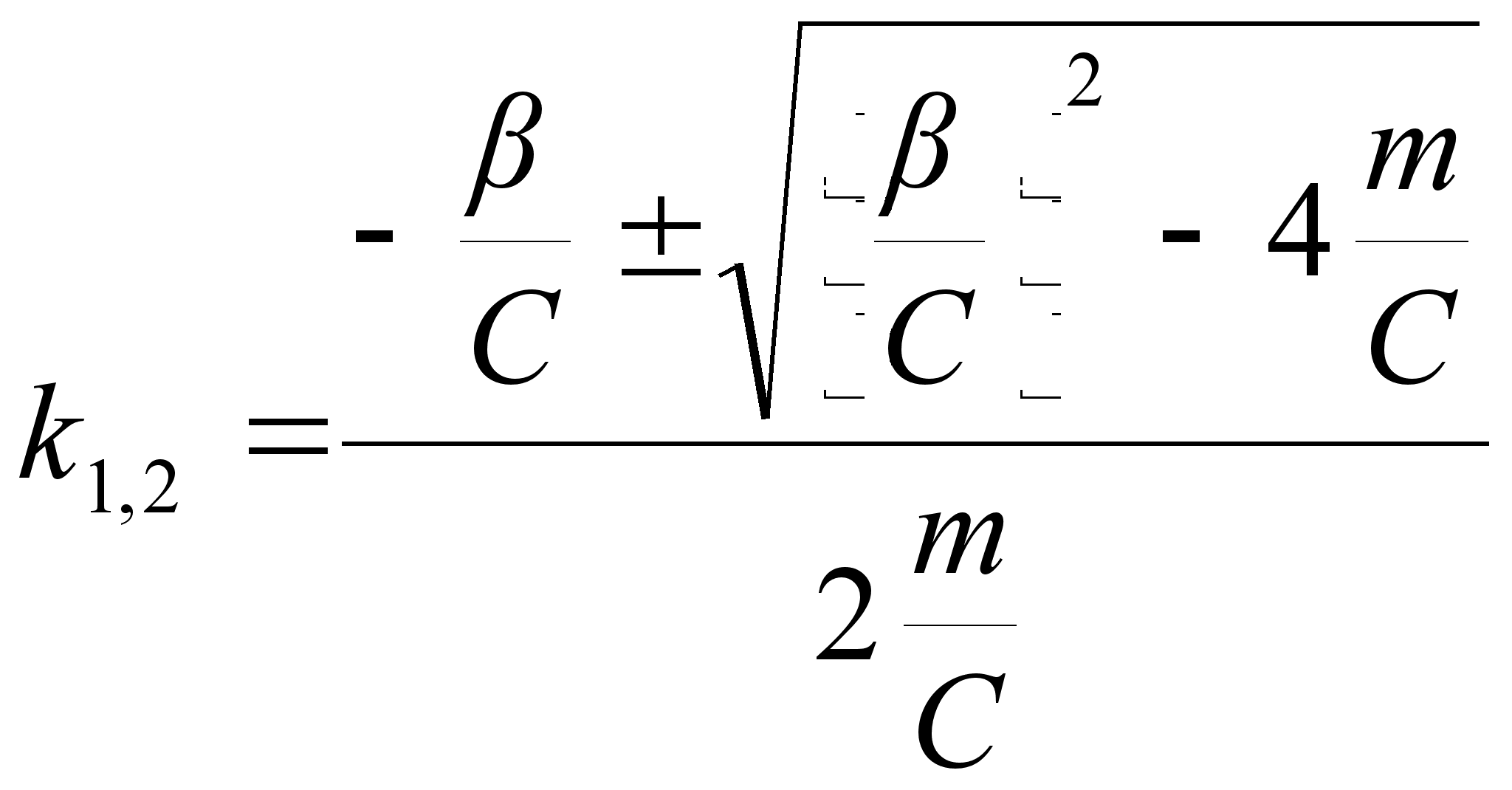
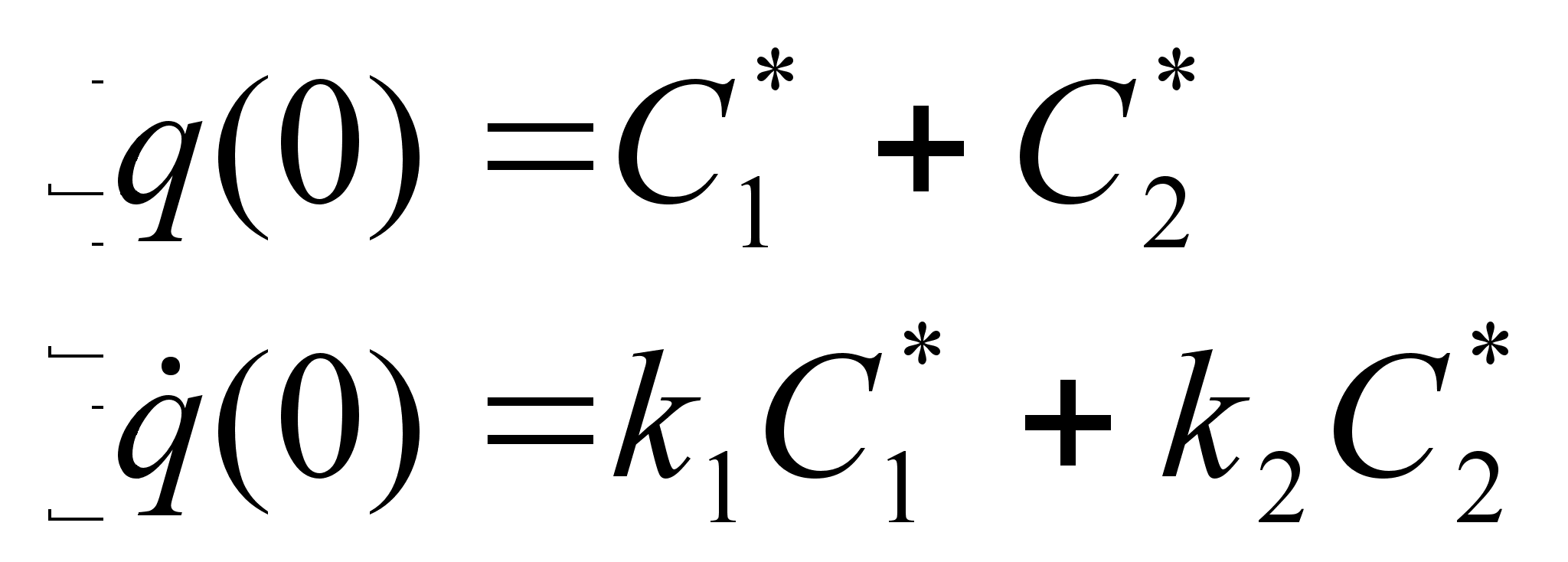 .
.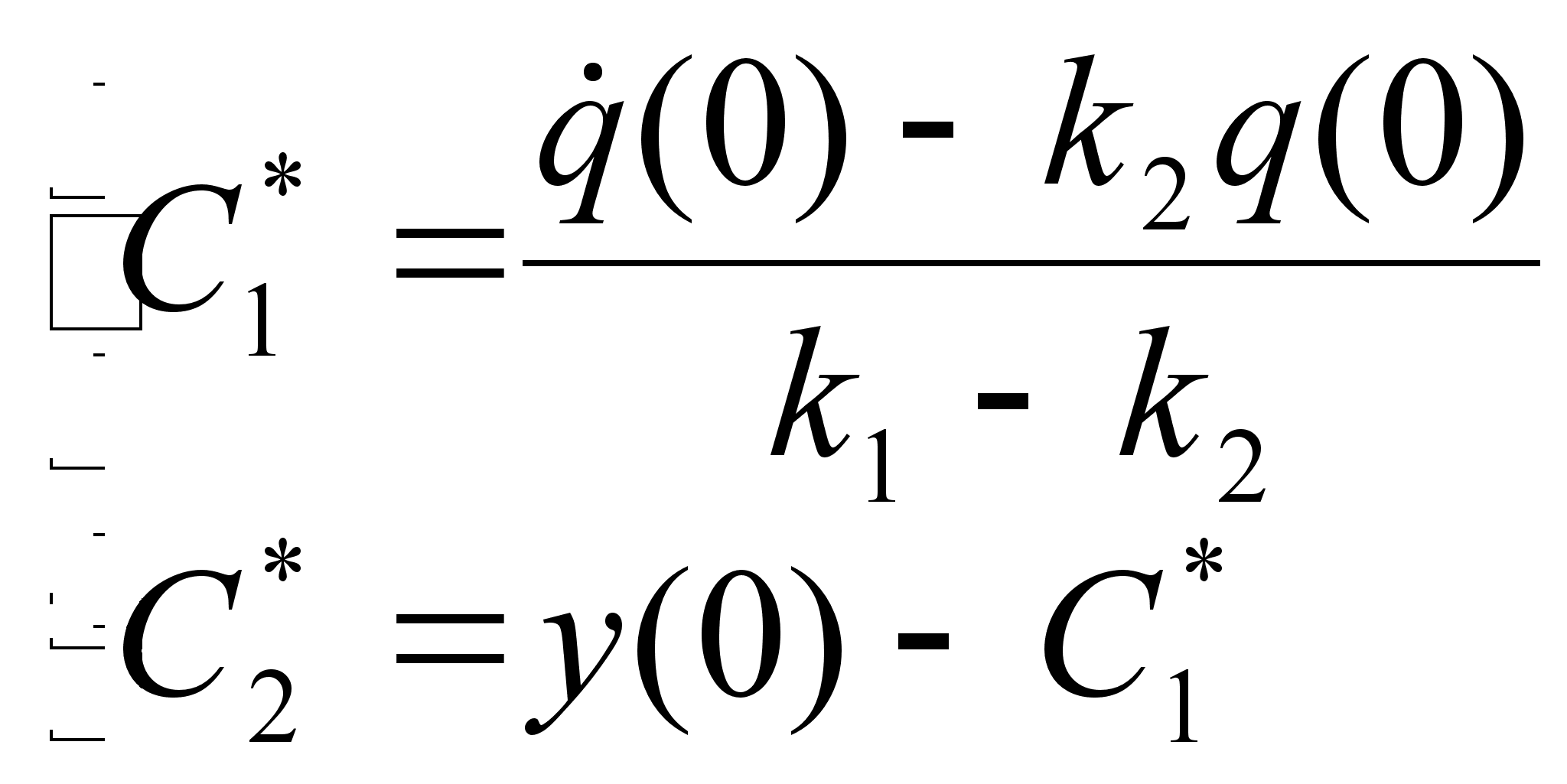 ,
,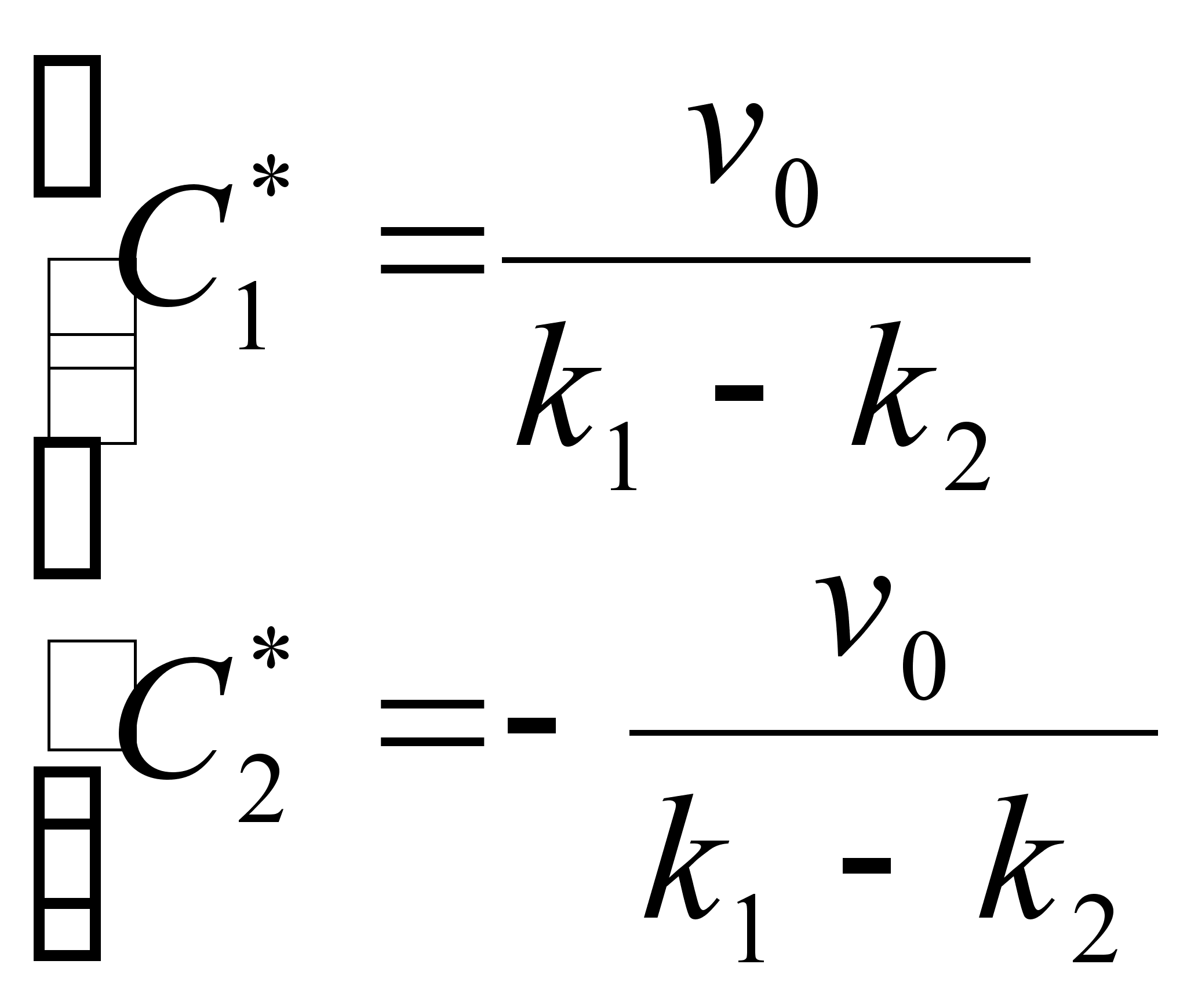
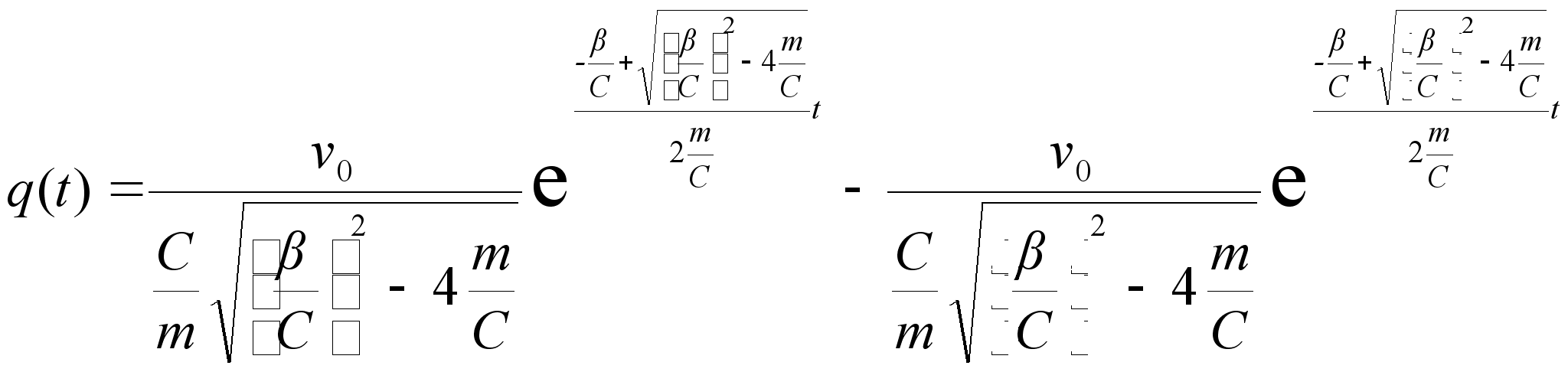
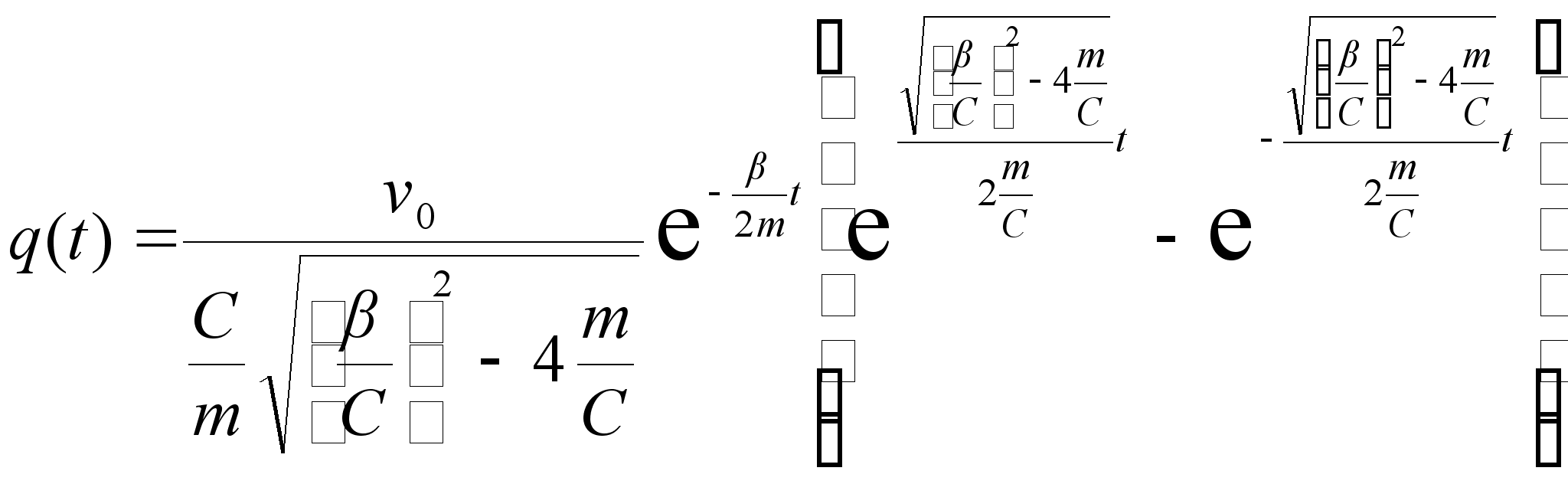 .
.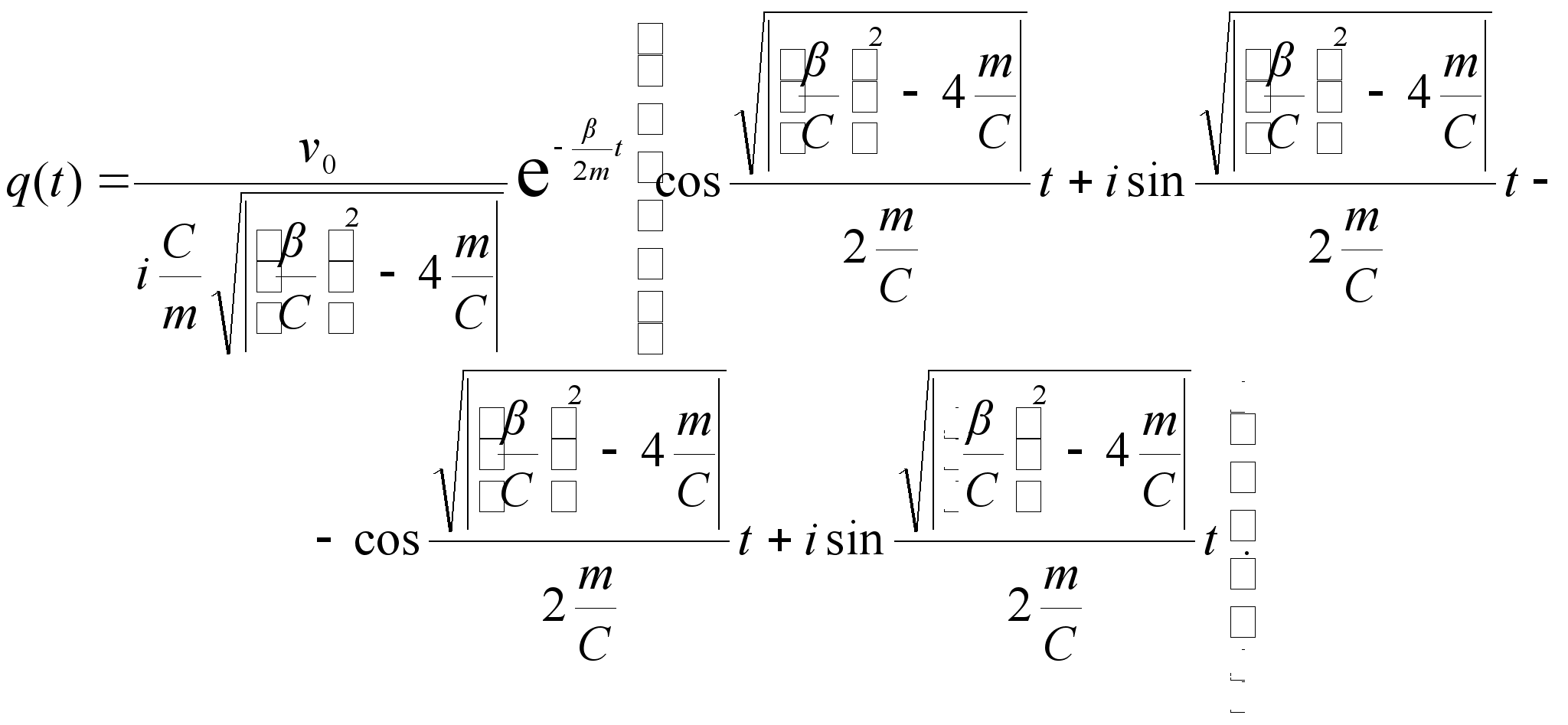
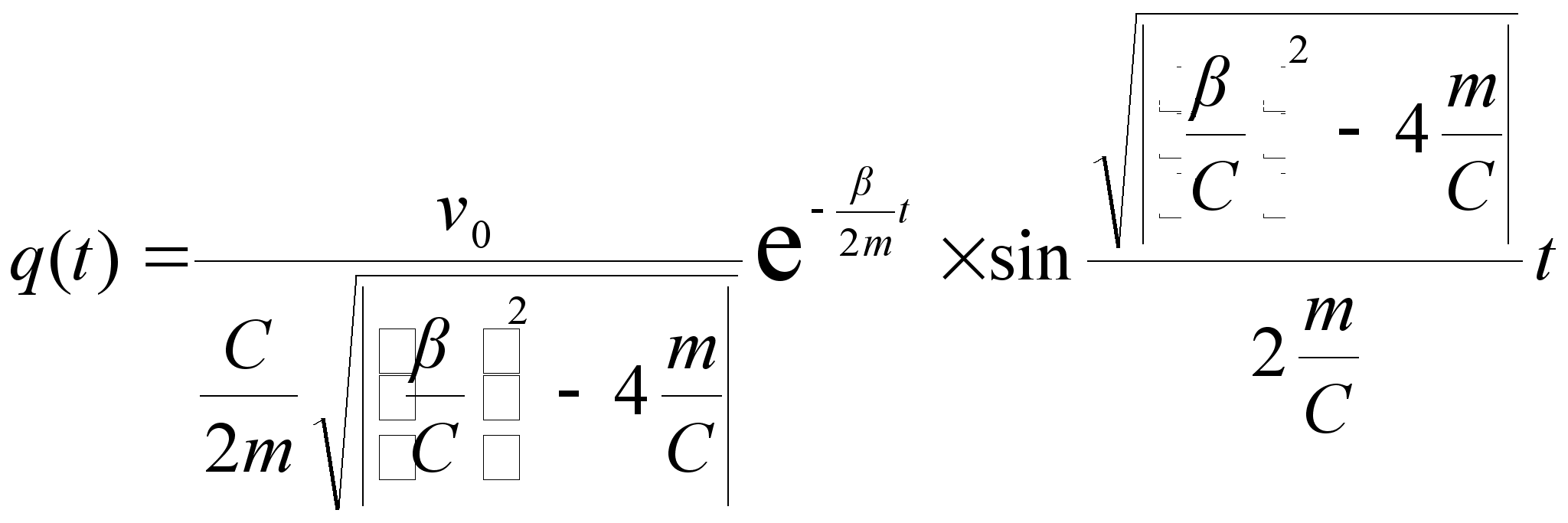
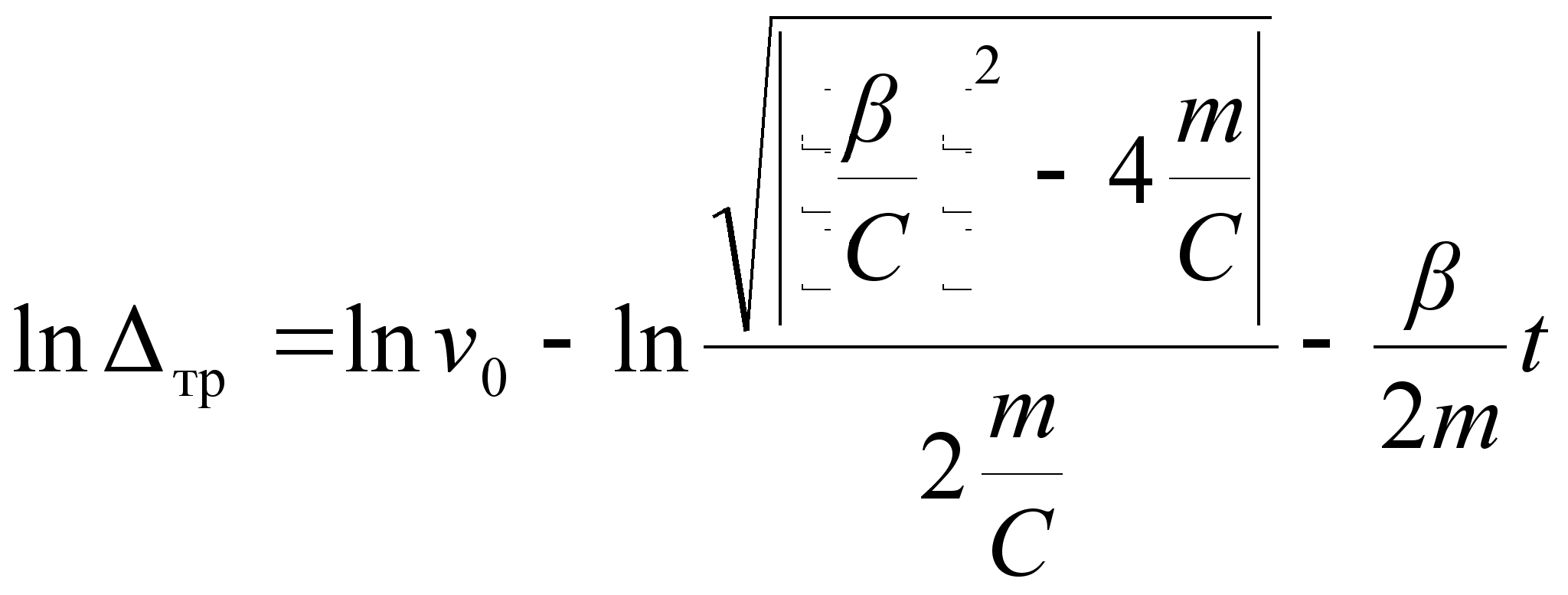 ,
,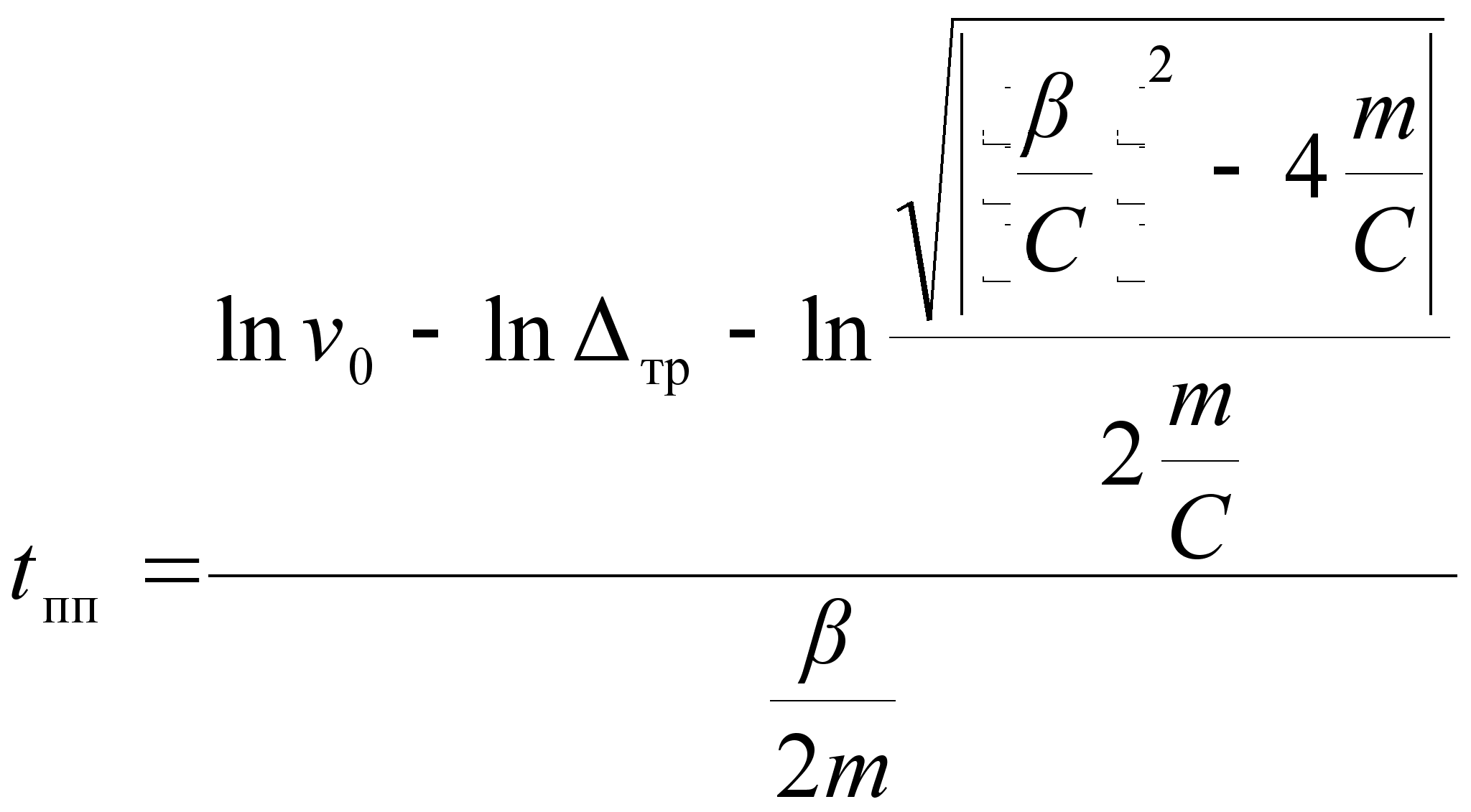


0 комментариев