ВЕЩЕСТВО И МАССА, ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
ВЗАИМОДЕЙСТВИЕ. ПОЛЕ. ПРИНЦИПЫ БЛИЗКОДЕЙСТВИЯ И ДАЛЬНОДЕЙСТВИЯ
СОСТОЯНИЕ СИСТЕМЫ, ЕЕ ИЗМЕНЕНИЕ ВО ВРЕМЕНИ
КЛАССИЧЕСКАЯ МЕХАНИКА
Принцип относительности Галилея. Преобразования Галилея
Законы классической механики и их инвариантность относительно преобразований Галилея
Детерминизм классической механики
РАБОТА, ЭНЕРГИЯ
СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Релятивистская механика
Релятивистская динамика, масса покоя, связь массы и энергии
ЗАКОНЫ СОХРАНЕНИЯ
Фундаментальные законы сохранения
Эволюция закона сохранения массы - энергии - материи
Навигация
Релятивистская механика
Концепция современного естествознания
113437
знаков
2
таблицы
5
изображений
12.2 Релятивистская механика.
Обратимся к преобразованиям Лоренца (12.1). Из них следует, что максимальная скорость движения материальных систем ограничена скоростью света в вакууме с. Если бы скорость движения тела превысила скорость света, то, как следует из преобразований Лоренца, координаты и время станут мнимыми т.е. потеряют реальный физический смысл.
Теперь рассмотрим некоторые следствия из преобразований Лоренца. В классической механике расстояние между двумя точками и время были одинаковым во всех инерциальных системах отсчета. В релятивистской механике они оказались разными в различных инерциальных системах отсчета, т.е. перестали быть инвариантами. Но инварианты относительно преобразований Лоренца должен быть. Одним из них является скорость света в вакууме - с. Она действительно одинакова во всех инерциальных системах отсчета. Другим инвариантом этих преобразований является так называемый интервал между событиями. Его квадрат равен: 
.
Благодаря инвариантности интервала пространство и время оказываются взаимосвязанными. Они образуют единое четырехмерное пространство-время. Вдоль четвертой оси откладывается мнимая величина 
. Четырехмерное пространство-время было впервые введено Г.Минковским (1864-1909) и сейчас носит его имя. Попробуем представить себе такое пространство. Мы умеем делать проекции трехмерного пространства на двухмерное. Например, таким образом мы рисуем на доске трехмерную систему координат на плоскости - двухмерном пространстве. Представим себе в объемном трехмерном пространстве проекцию четырехмерного куба. Это будут два куба, каждая из вершин одного куба соединена с соответствующей вершиной второго куба линией четвертого измерения. Расстояние между двумя точками в четырехмерном пространстве и будет интервал в соответствии с законами геометрии.
Проанализируем теперь на основе преобразований Лоренца одновременность событий в разных системах отсчета. В классической механике использовался принцип дальнодействия, когда взаимодействие между телами осуществлялись мгновенно через любое расстояние. В этом случае мы могли бы ставить одно и тоже время в разных системах координат. Попросту говоря синхронизовать время и задавать его одним и тем же.
1 1 2
 | |||||
 |  | ||||
2
Рис.12.2
Рассмотрим эксперимент по синхронизации часов, базируясь на постулатах теории относительности. Представим себе следующую ситуацию (см. рис.12.2). Первый наблюдатель 1 стоит на земле и мимо него двигается вагон, в середине которого стоит второй наблюдатель 2. В начале и конце вагона расположены часы (1) и (2) которые нужно синхронизовать. Это проще всего сделать следующим образом. Второй наблюдатель в вагоне посылает свет в две стороны и в момент прихода света на часы, они включаются с нуля и идут синхронно. С точки зрения наблюдателя в вагоне часы показывают одинаковое время. Рассмотрим, что покажут часы первому наблюдателю, стоящему на земле.
Скорость распространения света постоянна в любой системе отсчета. Пока свет распространяется в конец вагона, часы 1 переместятся ему навстречу и будут включены раньше. Часы 2 уйдут за время распространения света и будут включены позднее. Таким образом, с точки зрения первого наблюдателя часы будут показывать разное время , а с точки зрения второго наблюдателя - одинаковое. Время будет разное для двух разных наблюдателей, находящихся в различных инерциальных системах отсчета.
К этому же результату можно прийти и чисто формально, при помощи преобразований Лоренца. Покажем это. Пусть в неподвижной системе отсчета К два события происходят одновременно, т.е. 
. Найдем разность 
в системе отсчета К’, перемещающейся относительно К вдоль оси x со скоростью u. Для этого воспользуемся преобразованием Лоренца для времени.
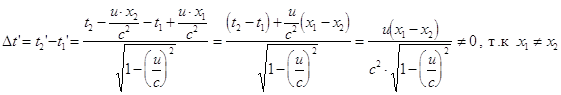
Не вдаваясь в детальный анализ, укажем, что изменение длительности промежутков времени не касается принципа причинности: если из двух событий, одно является следствием другого и разделены промежутком времени, то в любой инерциальной системе отсчета эти события также разделены промежутком времени, и последовательность событий не нарушается. Т.е. следствие всегда идет после причины.
Рассмотрим парадокс, следующий из преобразований Лоренца. Пусть в одной точке пространства в системе отсчета К произошли два события (например рождение и смерть человека) в моменты времени t1 и t2, соответственно. Промежуток времени между этими событиями в системе отсчета К равен 
. В движущейся системе отсчета K’ промежуток времени между этими событиями другой, что следует из преобразований Лоренца для времени. Теория относительности позволяет связать длительности промежутков времени в системе отсчета наблюдателя 
и в системе отсчета, связанной с наблюдаемыми объектами 
(собственное время).
.
В разных системах отсчета, двигающихся относительно друг друга время течет по разному, причем в системе отсчета, связанной с объектом наблюдения часы идут медленнее всего, т.е. собственное время всегда минимальное. Собственное время - еще один инвариант преобразований Лоренца, в какой бы инерциальной системе отсчета его ни вычисляли, всегда должен получиться одинаковый результат. Формула (12.3) неоднократно обыгрывалась в фантастических романах, когда отец улетал к звездам на космолете с большой скоростью, возвращался обратно молодым, а его сын, остававшийся на Земле уже успевал состарится.
Обратимся еще раз к примеру, приведенному в параграфе 12.1, в котором рассматривалось взаимодействие двух движущихся зарядов, и ответим на вопрос, почему же все-таки силы взаимодействия окажутся для разных наблюдателей разными. Ответ на него заключается в том, что в движущейся системе отсчета время течет медленнее, и ускорение, а значит, и сила взаимодействия уменьшится.
Кроме изменения хода часов наблюдается изменение размеров (укорочение) быстро движущихся объектов. Этот эффект тоже может быть выведен из преобразований Лоренца. Связь длины отрезка, направленного вдоль скорости движения, в системе К (наблюдаемая длина 
) и в системе K’ (собственная длина 
) задается формулой:
.
Таким образом собственная длина всегда максимальна. Отметим, что сокращаются лишь размеры тела вдоль направления скорости системы K’. Изменение размеров - кажущийся, ненаблюдаемый эффект. Размеры мы определяем, сравнивая длину линейки с размерами тела. Но, и сама линейка в другой системе координат будет менять свои размеры одновременно с телом. Этот эффект напрямую нельзя наблюдать.
Как ни странно, именно сокращение длины и замедление хода времени, предсказанные в теории относительности, удалось наблюдать еще в 30-е годы нашего века. Исследовались нестабильные частицы m-мезоны. Время жизни m-мезонов было измерено, 
. За это время частица могла пролететь расстояние не превышающее 
. Однако, m-мезоны могли рождаться лишь на высоте 20-30 км при столкновении космического излучения с ядрами атомов в атмосфере. Казалось бы, все они должны распасться еще в верхних слоях атмосферы, но приборы на земле уверенно регистрировали их. Объясняется это тем, что рождались они с очень большими скоростями, близкими к скорости света. В соответствии с формулой (12.3) течение времени в их их системе отсчета замедлялось и они успевали пройти расстояние в несколько десятков километров. Но как объяснить это же явление, если наблюдать за частицами в их собственной системе отсчета, ведь в этой системе время жизни частиц составляет действительно . А в этом случае для частиц сокращается длина пройденного ими пути. m-мезоны пролетают десятки километров и достигают земли, но для них в полном соответствии в формулой (12.4) длина этого пути сокращается до нескольких сотен метров. Таким образом, наблюдение одного природного явления подтвердило сразу два, казалось бы, абсурдных следствия из преобразований Лоренца.
В настоящее время существуют очень точные часы, которые показали, что время на движущихся искусственных спутниках Земли отстает от земного времени на 1 секунду за 44 года.
В релятивистской механике предсказан еще целый ряд парадоксальных с точки зрения классической механики явлений. В настоящее время большинство из них наблюдались в экспериментах. При этом не наблюдалось отклонений от предсказаний специальной теории относительности.
Похожие работы
... инерциальных системах отсчета. Пространственно-временной континуум – неразрывная связь пространства и времени и их зависимость от системы отсчета. Тема 11. Основные концепции химии 1. Химия как наука, ее предмет и проблемы Важнейшим разделом современного естествознания является химия. Она играет большую роль в решении наиболее актуальных и перспективных проблем современного общества. К ...
... сущность теории химической эволюции и биогенеза. Опишите историю открытия и изучения клетки. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету КОНЦЕПЦИИ СОВРЕМЕННОГО ЕСТЕСТВОЗНАНИЯ Билет № 30 Назовите и охарактеризуйте междисциплинарные естественные науки. Сформулируйте третий закон механического движения Ньютона. Каким ...
... вещей (»арден 1987: 53-68, Назаретян 1991: 60, Абдеев 1994: 150- 160). Атрибутивная концепция информации - информация как мера упорядоченности структур и их взаимодействий на всех стадиях организации материи (Абдеев 1994: 162). Одна из самых сложных проблем современного естествознания - функционирование отражения в неживом мире (существует ли в неживом мире опосредующее звено между ...
... , или концепция биогенеза). В XIX веке ее окончательно опроверг Л. Пастер, доказав, что появление жизни там, где она не существовала, связано с бактериями (пастеризация – избавление от бактерий). 3. Концепция современного состояния предполагает, что Земля и жизнь на ней существовали всегда, причем в неизменном виде. 4. Концепция панспермии связывает появление жизни на Земле с ее занесением из ...
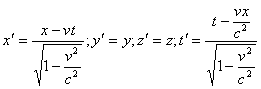
0 комментариев