Навигация
Построение математической модели
3. Построение математической модели.
. Регрессионный анализ.
Для построения математической модели выдвинем гипотезу о наличии линейной зависимости между прибылью и фактором времени, на нее влияющим. Следовательно, математическая модель может быть описана уравнением вида:
![]() , (3.1)
, (3.1)
где
![]() - линейно-независимые
постоянные
коэффициенты.
- линейно-независимые
постоянные
коэффициенты.
Для их отыскания применим регрессионный анализ. Результаты регрессии сведены в табл. 3.2 – 3.4.
Таблица 3.2 – Регрессионная статистика
| Множественный R | 0,096181456 | |
| R-квадрат | 0,009250873 | |
| Нормированный R-квадрат | -0,012287152 | |
| Стандартная ошибка | 537056,4999 | |
| Наблюдения | 48 | |
Таблица 3.3. –Дисперсионная таблица
| df | SS | MS | F | Значимость F | |
| Регрессия | 1 | 1,23884E+11 | 1,23884E+11 | 0,429513513 | 0,515492131 |
| Остаток | 46 | 1,32678E+13 | 2,8843E+11 | ||
| Итого | 47 | 1,33916E+13 |
Таблица 3.4 – Коэффициенты регрессии.
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y | 672637,41 | 157489,387 | 4,27100 | 9,65555E-05 | 355628 | 989646, | 355628 | 989646 |
| X | -3667,1732 | 5595,55298 | -0,65537 | 0,51549 | -14930,4 | 7596,07 | -14930,4 | 7596,07 |
Таким образом, уравнение, описывающее математическую модель, приобретает вид:
Y= 672637,4113-3667,173252X1. (3.2)
F-критерий из табл. 3.3 показывает степень адекватности, полученной математической модели.
4. Временной анализ и прогнозирование.
По условию задания необходимо проанализировать прибыль предприятия за четыре года его работы, и на основе полученных данных построить прогноз на пятый год. Для решения поставленной задачи воспользуемся методом временных рядов.
Для расчета сезонных индексов зададимся мультипликативно-аддитивной моделью тренда:
Y=kX+b, (4.1)
и, используя метод простой линейной регрессии, построим гипотетическую модель (Приложение А). Отклонения от модели, выраженные в процентах, представлены в табл. 4.1.
Таблица 4.1 – Отклонение от модели
| 1994 | 1996 | 1997 | 1998 | |
| Январь | 224% | 264% | 241% | 317% |
| Февраль | 135% | 137% | 154% | 225% |
| Март | 106% | 97% | 96% | 87% |
| Апрель | 46% | 20% | 44% | 42% |
| Май | 61% | 49% | 18% | 0% |
| Июнь | 38% | 74% | 27% | 48% |
| Июль | 31% | 100% | 24% | 63% |
| Август | 23% | 125% | 26% | 69% |
| Сентябрь | 47% | 50% | 46% | 30% |
| Октябрь | 39% | 44% | 64% | 20% |
| Ноябрь | 63% | 77% | 83% | 52% |
| Декабрь | 318% | 291% | 185% | 383% |
Для того чтобы рассчитать прогноз на следующий год, рассчитаем сезонные индексы по табл. 4.1, а затем, по уравнению тренда, найдем теоретические значения прибыли на следующий год. Для получения окончательного прогноза проведем нормирование, умножив значения тренда на сезонные индексы. Значения расчетов приведены в табл. 4.2.
Таблица 4.2 – Результаты прогноза.
| Сезонные индексы | Тренд | Прогноз на 1999 | |
| Январь | 209% | 492946 | 1031069 |
| Февраль | 130% | 489279 | 637311 |
| Март | 77% | 485612 | 374399 |
| Апрель | 30% | 481944 | 146354 |
| Май | 26% | 478277 | 122574 |
| Июнь | 37% | 474610 | 177951 |
| Июль | 43% | 470943 | 204531 |
| Август | 49% | 467276 | 227353 |
| Сентябрь | 35% | 463609 | 160283 |
| Октябрь | 33% | 459941 | 153419 |
| Ноябрь | 55% | 456274 | 250688 |
| Декабрь | 235% | 452607 | 1064985 |
График прогнозируемой прибыли представлен в Приложении Б.
ВЫВОДЫ
В результате проведенной работы был произведен статистический анализ исходных данных, полученных при исследовании основных показателей деятельности предприятия, с целью выявления доминирующих факторов влияющих на прибыль и построена адекватная математическая модель и спрогнозирована прибыль на последующие периоды.
В процессе выполнения работы изучили и научились применять на практике следующие методы математической статистики:
линейный регрессионный анализ,
множественный регрессионный анализ,
корреляционный анализ,
проверка стационарности и независимости выборок,
метод временных рядов,
выявление тренда,
критерий ![]() .
.
Перечень ссылок
Бендод Дж., Пирсол А. Прикладной анализ случайных данных: Пер. с англ. – М.: Мир, 1989.
Математическая статистика. Под ред. А. М. Длина, М.: Высшая школа, 1975.
Л.Н.Большев, Н.В.Смирнов. Таблицы математической статистики.-М.: Наука, 1983.
Н.Дрейпер, Г.Смит. Прикладной регрессионный анализ. Пер. с англ.- М.: Статистика, 1973.
ПРИЛОЖЕНИЕ А
Г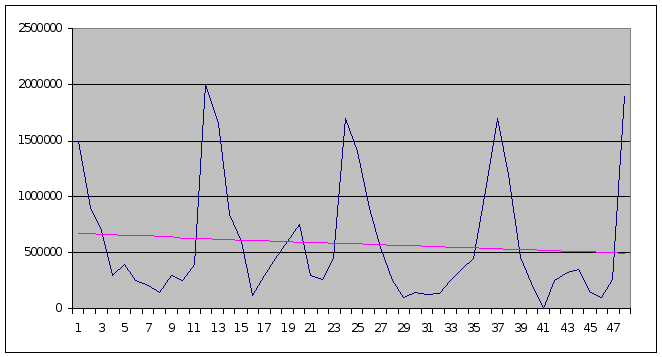
рафик
зависимости
колебаний
прибыли предприятия
от времени.
Рисунок А.1 – График зависимости прибыли предприятия от времени.
ПРИЛОЖЕНИЕ Б
График прогноза изменения прибыли по месяцам.
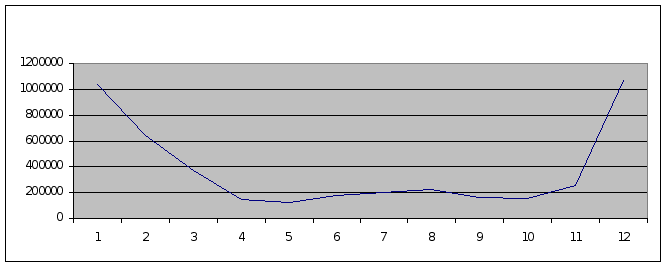
Рисунок Б.1 – График прогноза изменения прибыли по месяцам.
УДК
КП
Министерство образования Украины
Харьковский государственный технический университет радиоэлектроники
Кафедра ПОЭВМ
Комплексная курсовая работа
по курсу «Вероятностные процессы и математическая статистика в автоматизированных системах»
Тема: «Провести экономическую оценку эффективности работы предприятия. Провести долгосрочное планирование работы методом множественной линейной регрессии. Построить математическую модель повышения эффективности работы».
Выполнил:
Ст. гр. ПОВТАС-96-3 Фурсов Я. А.
Руководитель: асс. Шамша Т. Б.
Комиссия: проф. к. т. н. Дударь З. В.
проф. к.. т. н. Лесная Н. С.
асс. Шамша Т. Б.
1999
РЕФЕРАТ
Пояснительная записка к комплексной курсовой работе: 30 с.,
Похожие работы
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
... ПО “Уралмаш”, “АвтоВАЗ”, МИИТ, Казахского политехнического института, Донецкого государственного университета и многих других. Затем Институт в качестве Лаборатории эконометрических исследований разрабатывал эконометрические методы анализа нечисловых данных, а также процедуры расчета и прогнозирования индекса инфляции и валового внутреннего продукта. Институт высоких статистических технологий и ...
... на задний план традиционными постановками. Несколько лет назад при описании современного этапа развития статистических методов нами были выделены [29] пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять "точек роста": непараметрика, робастность, бутстреп, интервальная статистика, статистика объектов нечисловой природы. Обсудим их. 5. ...
... и боятся бедности и как следствие воспитывают своих детей в такой же привычке к труду и благосостоянию, а удача доставляет удовлетворение их родительским чувствам и самолюбию. Принадлежит первое в истории экономической мысли достаточно глубокое теоретическое обоснование положений о капитале. Считал, “что деньги сами по себе представляют собой бесплодное богатство, которое ничего не производит”. ...
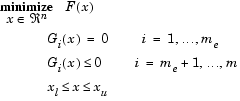

0 комментариев