СТАТИСТИКА

Министерство по налогам и сборам Российской Федерации

В с е р о с с и й с к а я г о с у д а р с т в е н н а я н а л о г о в а я а к а д е м и я

СТАТИСТИКА

 

КОНТРОЛЬНая работа

 Выполнила: студентка группы К4

Фак-та Управления

Могученко Анна Павловна

Проверил: Соколин В.П.

Москва – 2001

Задача 1

Требуется определить значения следующих показателей:

1. Средняя трудоемкость изготовления изделия

2 Средний уровень выработки

3. Средний уровень оплаты труда

4. Средний уровень фондоотдача

 

Рассчет в таблицах 1,2,3,4.

 

Методические указания

Расчёт средних по результатам группировки.

Данные для расчета и анализа средних величин могут быть представлены в сгруппированном виде, когда для каждого значения усредняемого признака Х сообщается частота его повторения. В этих случаях средняя величина рассчитывается по обычным формулам средних взвешенных (арифметических либо гармонических). Если в сгруппированных данных указывается не конкретное значение признака Х по каждой группе, а лишь интервал его изменения, то в этом случае необходимо получить среднее значение признака по каждой группе. А далее используются обычные формулы средних взвешенных. Если же средние значения признака в группах определить по имеющимся сведениям нельзя, то их заменяют условно значениями центра интервалов. В результате получают ряд распределения, аналогичный дискретному, где в качестве значений дискретного признака будут выступать центры интервалов а_i, а в качестве весов признака F_i  - количество элементов ряда для интервала i.

Таким образом, расчет средней арифметической делают по формуле

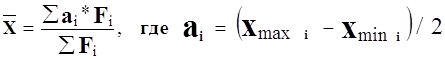
Показатель себестоимости является вторичным признаком, так как он задан на единицу первичного признака (объем продукции, выраженный абсолютной величиной) и может быть представлен как отношение двух первичных признаков, а именно затрат на производство и объём продукции:

С = ЗП / ОП, где С — себестоимость, ЗП — затраты на производство, ОП —. объем продукции.

Следовательно, для расчета средней себестоимости по каждому предприятию следует вычислить среднюю взвешенную. Нужно выбрать: арифметическую или гармоническую?

Выбор вида средней усредняемого признака выполняется по следующим правилам.

1. Если в условии задачи даны численные значения числителя и знаменателя логической формулы показателя, средняя величина вычисляется непосредственно по этой формуле.

2. Если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить среднюю величину, и при этом известны численные значения знаменателя её логической формулы, а значения числителя не известны, но могут быть найдены как произведения этих показателей, то средняя должная вычисляться по формуле средней арифметической взвешенной.

3. Если известны численные значения числителя логической формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя вычисляется по формуле средней гармонической.

 Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности — носители признака, а произведения этих единиц на значения признака (т. е. m = X*f). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т. д.) предприятиям, рабочим, занятым изготовлением одного итого же вида продукции, одной и той же детали, изделия.

Общее требование к формуле расчета среднего значения состоит в том, чтобы все этапы расчета имели реальное содержательное значение. Полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей. Иначе говоря, средняя величина должна исчисляться так, чтобы при замене каждого индивидуального значения усредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный с усредняемым. Этот итоговый показатель является определяющим в том смысле, что его связь с индивидуальным значением признака определяет способ расчета средней величины.

 

Расчет средних через показатели структуры

Средние арифметические и средние гармонические могут быть как простыми, так и взвешенными. Веса в формулах средних показывают повторяемость данного значения признака.

Величина средней зависит не от самих абсолютных значений весов отдельных элементов, а от пропорций между ними. Поэтому вместо абсолютных значений для взвешивания можно брать веса вариантов, выраженные в долях единицы или в процентах. Допустим, что требуется вычислить среднюю величину для некоторой совокупности вариантов (x₁ + x₂+...+ x_n) с соответствующи­ми частотами (n₁ + n₂+...+ n_n). Отношения отдельных частот n₁, n₂ и т. д. к сумме частот представляют доли рi отдельных вариантов из всей совокупности или удельные веса этих вариантов (частности).

Можно записать, что X = X1*p1+Х2* р2+...+Хп*рп= ∑х_i * р_i ;
 т. е. мы от абсолютных значений весов частот перешли к относительным (частностям).

Из этого свойства вытекает очень важное практическое правило. Если неизвестны абсолютные значения весов, но известны пропорции между ними, то мы можем пользоваться этими пропорциями для взвешивания. Допустим, что одно предприятие будет выпускать продукт по цене 10 руб., а второе - этот же продукт по цене 15 руб. Неизвестно точно, сколько продукции выпустит каждое предпри­ятие, но известно, что второе предприятие выпустит продукции в 2 раза больше, чем первое. Тогда можно вычислить среднюю цену так: х = (10 *1 + 15 *2) / 3= 13,3 руб.

То же правило применяется в тех случаях, когда неизвестны абсолютные величины весов, но известны какие-то другие значения, которые связаны с этими весами. Вместо абсолютных значений можно брать эти производные величины. Например, если известно, что на первом предприятии в 2 раза больше рабочих, чем на втором, то можно условно предположить, что и продукции первое предприятие выпускает больше, чем второе тоже вдвое.

Если удельные веса заданы не в долях, а в процентах, тогда:

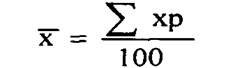
где р - удельный вес каждого варианта в процентах.

1.   Средняя трудоемкость изготовления изделия одного и того же вида несколькими рабочими (t):

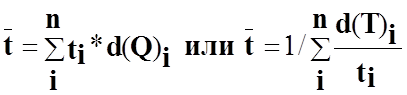где t, — трудоемкость изготовления единицы продукции конкретным рабочим;

d(Q)— доля рабочего в общем объеме произведенной продукции;

d(T) — доля рабочего в общих затратах рабочего времени.

Средняя трудоёмкость изготовления изделия

Таблица1

Рабочий	Трудоёмкость изготовления изделия, чел. час./ шт.	Центральное значение интервала,  чел. час./шт.	Объем продукции, штук	Доля рабочего в общем объеме произведенной продукции, %	Затраты рабочего времени, чел. час.	Доля рабочего в общих затратах рабочего времени, %,
1	2	3	4	6	5	7
1.	9-12	10,5	30	35	350	20
2.	12-15	13,5	26	26	160	29
3.	15-18	16,5	32	23	390	34
4.	18 — 21	19,5	47	16	280	17
Итого:		---	135	100 %	1180	100 %
Средняя трудоёмкость изготовления изделия, чел. час./шт.			15,67	14,11	14,30	14,29

1)

2)

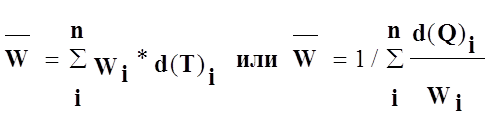2. Средний уровень выработки продукции в единицу рабочего времени (W).

Рассчитывается он по формулам

где W—уровень выработки для отдельного объекта (предприятия, цеха, участка, рабочего);

d(Т) — доля данного объекта (предприятия, цеха, участка, рабочего) в общих по всей совокупности затратах рабочего времени;

d(Q) — доля объекта i в общем выпуске продукции.

Средний уровень выработки на одного рабочего

 Таблица 2

Рабочий		Выработка на одного рабочего,  шт. / день	Центральное значение интервала,  шт. / день		Объем продукции, штук		Доля рабочего в общем объеме произведенной продукции, %		Затраты труда рабочего, чел. дней.		Доля рабочего в общих затратах труда рабочего, %,
1		2	3		4		5		6		7
1.		7 - 8	7,5		15		34		14		34
2.		8 - 9	8,5		29		29		26		11
3.		9 - 10	9,5		38		19		37		26
4.		10 - 11	10,5		57		18		54		29
	Итого:			--		139		100		131		100
	Средняя выработка на одного рабочего,  шт. / день			---		9,9		9,0		9,7		9,0

1)

2)

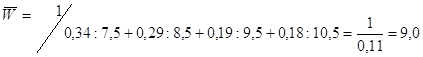
3. Средний уровень оплаты труда (Т):

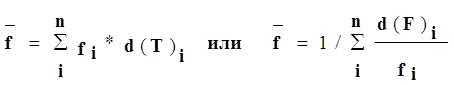
,где f — уровень оплаты в единицу времени на объекте i;

d(Т) — доля объекта i. в общих трудозатратах;

d(F)—доля объекта i в общем суммарном фонде оплаты труда.

Средний уровень оплаты труда рабочего

Таблица 3

Рабочий		Уровень оплаты труда рабочего, тыс. руб. / мес.	Центральное значение интервала,  шт. / день		Фонд оплаты труда, тыс. руб.		Доля рабочего в общем Фонде оплаты труда, %		Затраты труда рабочего, чел. мес.		Доля рабочего в общих затратах труда рабочего, %,
1		2	3		4		6		5		7
1.		1 – 3	2		16		18		18		29
2.		3 – 5	4		29		34		27		34
3.		5 – 7	6		64		29		16		11
4.		7 - 9	8		159		19		19		26
	Итого:			--		268		100		80		100
	Средний уровень оплаты труда рабочего, руб. / мес.			---		5,88		4,05		5,44		4,68

1)

2)

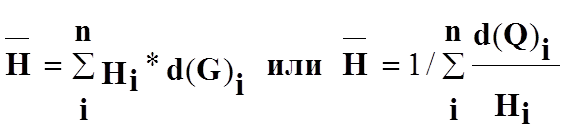4. Средний уровень фондоотдачи (Н):

где Н — уровень фондоотдачи (стоимость произведенной продукции, руб.) на 1 руб. основных производственных фондов по объекту (отрасли, предприятию) i;

d(G) — доля объекта i в общей стоимости фондов по всей изучаемой совокупности;

d(Q) — доля объекта i в общем выпуске продукции.

 

 

 

 

 

 

Средний уровень фондоотдачи

 Таблица 4

Вид оборудования	Уровень фондоотдачи, руб. / на 1 руб. стоимости производственных фондов.	Центральное значение интервала,	Объем произведенной продукции, тыс. руб.	Доля оборудования в общей стоимости фондов, %	Стоимость основных производственных фондов, тыс. руб.	Доля оборудования в общем объеме выпуска продукции, %,
1	2	3	4	6	5	7
А.	1 – 3	2	164	31	325	18
Б.	3 – 5	4	117	24	450	19
В.	5 – 7	6	133	12	250	31
Г.	7 - 9	8	221	33	300	32
Итого:		--	635	--	1325
Средний уровень фондоотдачи		---	3,45	4,94	5,30	4,37

1)

2)

1. Средняя трудоёмкость изготовления изделия

d(Q)1=30:135=0,22; d(Q)2=26:135= 0,19 ;d(Q)3 = 32:135=0,24 ; d(Q)4=47:135=0,35

d(T)1=350:1180=0,3; d(T)2=160:1180=0,14; d(T)3=390:1180=0,33; d(T)4=280:1180=0,24

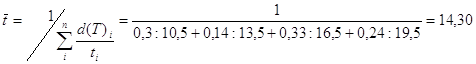
2. Средний уровень выработки на одного рабочего

d(Q)1=15:139=0,11; d(Q)2=0,21; d(Q)3=0,27; d(Q)4=0,41

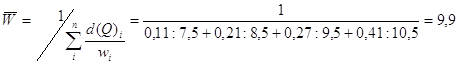
d(T)1=14:131=0,11; d(T)2=0,20; d(T)3=0,28; d(T)4=0,41