Абсолютное значение одного процента прироста

4. Абсолютное значение одного процента прироста

Показатель абсолютного значения одного процента прироста представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах. В буквенном выражении этот показатель может быть представлен в виде следующего соотношения:

(Xi - Xi – 1) / ∆Кприр. *100, где ∆Кприр. - цепной рост прироста.

Так как ∆Кприр. = (Xi - Xi –1) / Хi –1, то из приведенного выше соотношения нетрудно установить, что абсолютное значение одного процента прироста равно 0,01 предшествующего уровня.

Показатель абсолютного значения одного процента прироста играет весьма важную роль в экономическом анализе.

5. Исчислим средние показатели, характеризующие динамический ряд, т.е. изменение численности работников предприятия в среднем за 6 лет. Этими показателями являются средние или среднегодовые абсолютные приросты и средние или среднегодовые темпы роста. Исчисляются они по следующим формулам:

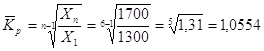
Среднегодовой темп роста исчислили по формуле через значения уровней ряда. Но для расчета этого показателя может применяться и другая формула - средняя геометрическая. Она основана на перемно­жении цепных темпов роста (так как проценты и коэффициенты нико­гда не суммируются, что является грубой ошибкой, их можно только перемножать):

Между цепными и базисными темпами роста существует следую­щее правило (взаимосвязь): произведение цепных темпов роста равно конечному базисному.

В нашем примере можно обойтись без перемножения, а взять из табл.5  последнее значение базисного темпа роста (отношение уровня 2000 г. к уровню 1995 г.). Оно равно 131,0%, или в коэффициентах 1,310.. Из этого числа извлекаем корень пятой степени и получаем 1,0554 , или 105,54%.

 

1,0554

Зная среднегодовой темп роста, можно определить среднегодовой темп прироста по формуле

Розничный товарооборот за период с 1995г. по 2000 г. в среднем возрастал за год на 5,54% (в абсолютном выражении - на 17 чел.).

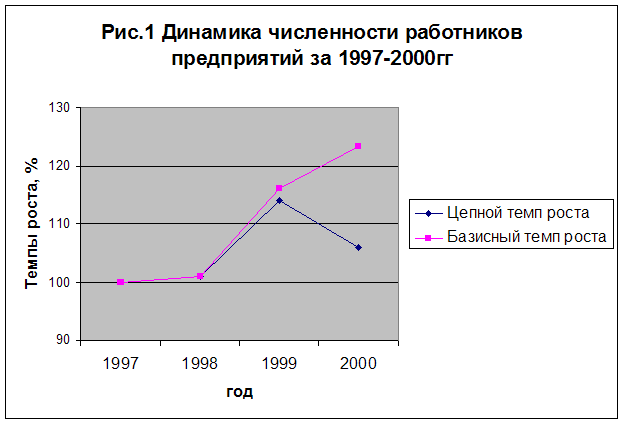
6. На основании исчисленных темпов роста (базисных и цепных) по­строим график (рис..1).

7. На основании расчетов и графика сделаем следующие выводы. Рассмотрим базисные темпы роста. Так, численность работников предприятия в 2000 г. по сравнению с 1995 г. возросла на 131%; в 1996,1997,1998 гг. численность возрастает довольно плавно и не значительно на 104,106,108 % соответственно.

Цепные показатели указывают на рост или снижение значения по сравнению с предшествующим годом. Так, в 1996г по сравнению с базисным возрасла на 104%. 1997 и 1998гг – тенденция к уменьшению численности. В 1999 г. по сравнению с 1998 резко подскачила численность (114%), а в 2000г. опять упал до 106%.

Задача 3

 

СЕЗОННЫЕ КОЛЕБАНИЯ. МЕТОД ПОСТОЯННОЙ СРЕДНЕЙ

По данным о выгрузке вагонов по отделению железной дороги (тыс. усл. ваг.) :

1) измерить сезонные колебания выгрузки вагонов по отделению железной дороги ( тыс. усл. ваг.), применяя соответствующую формулу индекса сезонности:

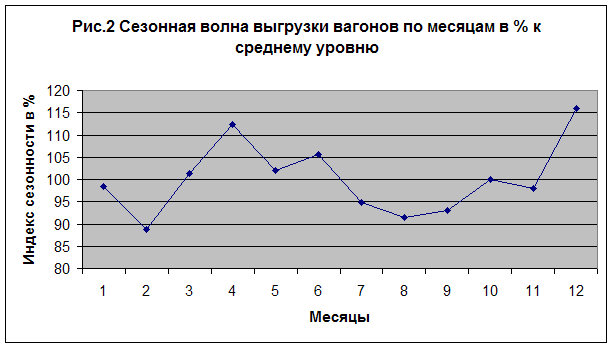
2) показатели сезонной волны изобразить графически;

3) на основе синтезированной модели сезонной волны сделайте прогноз объёмов выгрузки вагонов по отделению железной дороги (тыс. усл. ваг.) по месяцам 2001 г. возможного объёма работы в 500 (тыс. усл. ваг.).

Рассчеты представлены в таблице 6.

Методические указания

Сезонными называются периодические колебания, возникающие под влиянием смены времени года.

На изменение уровней ряда динамики внутри года (внутригодовой динамики) оказывают влияние периодические колебания, случайные отклонения и тренд, т.е. общая тенденция развития ряда динамики

Если изучаются сезонные колебания за отдельный год, то обычно тренд не принимается во внимание и отклонения месячных 30-дневных уровней исчисляются от среднемесячного уров­ня за год.

Для измерения сезонных колебаний важное значение имеет форма сезонной волны, изучаемая с помощью индекса сезонно­сти.

Существует несколько методов расчета индекса сезонности.

Для рядов внутригодовой динамики, в которых повышающий или понижающий тренд отсутствует или незначителен,
средний индекс сезонности определяется отношением месячных уровней

к среднемесячному за год по следующей формуле:

Применение этой формулы для расчетов индекса сезонности носит название способа постоянной средней, так как базой срав­нения для всех эмпирических уровней анализируемого ряда динамик является общий средний уровень.

Сезонные колебания выгрузки вагонов по отделению железной дороги (тыс. усл. ваг.)

 

Таблица 6

Год  Месяц	1997 уi	1998 уi	1999 уi	Всего за 3 года åуi	В среднем за 3 года	Индекс сезонности i si, %	Отклонение от среднего Di = уi - y	Квадрат отклонения Di2	Прогноз на 2001 г. уi
А	1	2	3	4	5	6	7	8	9
Январь	36,3	32,1	37,3	105,70	35,23	98,35	-0,59	0,35	40,98
Февраль	33,2	30,0	32,2	95,40	31,80	88,78	-4,02	16,16	36,99
Март	34,0	33	42	109,00	36,33	101,42	-0,51	0,26	42,26
Апрель	41,9	35,8	40,9	118,60	39,53	112,30	3,71	13,76	46,79
Май	36,8	29,1	36,8	102,70	36,57	102,09	0,75	0,56	42,54
Июнь	42,3	30,9	40,3	113,50	37,83	105,61	2,01	4,04	44,01
Июль	35,3	31,4	35,3	102,00	34,00	94,92	-1,82	3,31	39,55
Август	35,0	29,3	34	98,30	32,77	91,49	-3,05	9,30	38,12
Сентябрь	33,7	32,5	33,7	99,90	33,30	92,96	-2,52	6,35	38,74
Октябрь	36,9	35,6	34,9	107,40	35,80	99,94	-0,02	0	41,64
Ноябрь	35,3	34,7	35,3	105,30	35,10	97,99	-0,72	0,52	40,83
Декабрь	43,7	38,2	42,7	124,6	41,53	115,94	5,71	32,60	48,31
Итого:	444,4	392,6	445,4	1282,40	429,79	100,0	---	87,21	500,76
В среднем	37,03	32,72	37,12	106,87	35,82		---		41,67

Рассмотрим применение метода постоянной средней на примере данных таблицы 6.

Данные графы 1 берутся из таблицы исходных данных. Данные граф 2 и 3 остаются неизменными по всем вариантам расчета задания.

В графе 4 табл. 6 сначала суммируются данные по месяцам за три года: для января åу_i =36,3+32,1+37,3=105,7 и т.д.

По формуле простой средней арифметической для каждого месяца в графе 5 табл. 6 находим среднее значение выгрузки в среднем за три года:
для января =105,7 : 3 = 35,23 тыс. усл. ваг. и т.д.

В итоговой строке "В среднем" графы 5 определен также по формуле средней арифметической простой знаменатель формулы индекса сезонности в виде общего для всего ряда динамики среднего уровня за год:
=429,79 : 12 = 35,82 тыс. усл. ваг.

Этот общий средний уровень и используется в качестве постоянной базы сравнения при определении средних индексов сезонности, кото­рые определены в графе 6 табл. 6: за январь i_si= 35,23 : 35,82 * 100=96,03 %.

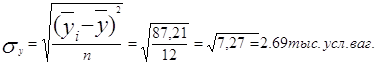Мерой сезонных колебаний является среднее квадратическое отклонение


Коэффициент сезонной колеблемости будет:

Характер сезонных колебаний показан на рис. 2. На графике видно, что сезонные колебания выгрузки вагонов характеризуются довольно-таки резким спадом в феврале (-9,57) и тут же резким скачком в марте (+12,64), еще один скачек в декабре (+17,95). В другие месяцы повышения и понижения гладкие.

На основе значений сезонной волны по месяцам выполним прогноз выгрузки вагонов по месяцам 2001 г., если общий объем работы равен за год 500 тыс. усл. вагонов.

Сначала определим средний месячный за год объем выгрузки:

Y = 500 : 12 = 41,67 тыс. усл. ваг.

Прогноз объемов выгрузки вагонов на каждый месяц требует полученную сумму 41,67 умножить на значения соответствующих индексов сезонности для каж­дого месяца.
 Например, для января 41,67 *0,9835 = 40,98тыс. усл. ваг.

Полученные результаты расчетов помещены в графе 9 табл.6.

Общая сумма реализации за все 12 месяцев равна исходной сумме 500 тыс. усл. ваг, что свидетельствует о правильности проведенных расчетов.

Задача 4.

 

СЕЗОННЫЕ КОЛЕБАНИЯ. МЕТОД СКОЛЬЗЯЩЕЙ СРЕДНЕЙ

По данным о выгрузке вагонов по отделению железной дороги (тыс. усл. ваг.) табл.6,7

1) определите характер общей тенденции динамики выгрузки вагонов по отделению железной дороги (тыс. усл. ваг.);

2) применяя соответствующую формулу среднего индекса сезонности, измерить сезонные колебания выгрузки вагонов по кварталам данного четырёхлетия;

3) показатели сезонной волны внутригодового цикла изобразить графически;

4) сделайте краткие выводы.

Рассчет в таблице 7,8.

Методические указания