Навигация
При изучении сезонных колебаний за ряд лет в которых наблюдается повышающий или понижающий тренд применяется методика скользящей средней
1. При изучении сезонных колебаний за ряд лет в которых наблюдается повышающий или понижающий тренд применяется методика скользящей средней.
В этом случае индекс сезонности за период определяется отношением эмпирических уровней за период времени к среднему за тот же период по следующей сглаженному уĈi формуле:
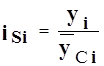
Применение этой формулы для расчетов индекса сезонности носит название способ скользящей средней.
В основу методов положено определение по исходным данным теоретических уровней, в которых случайные колебания погашаются (сглаживаются), а основная тенденция развития явления выражается в виде некоторой плавной линии
В практике встречаются случаи, когда уровень ряда динамики не обнаруживает явно выраженной тенденции роста или падения. Примером этому могут служить нижеприводимые данные о выгрузке вагонов. Чтобы охарактеризовать в подобных случаях основное направление изменения уровня ряда, применяют различные приемы и способы, в частности прибегают к укрупнению интервалов и механическому или аналитическому сглаживанию.
Подсчитав на основе исходных данных количество выгруженных вагонов за каждый квартал года, получим новый ряд динамики.
Этот новый ряд динамики отчетливо показывает, что объем выгрузки вагонов постепенно увеличивается, чего нельзя было сказать на основе месячных данных. Укрупнение интервалов позволило, таким образом, выявить в данном конкретном случае основное направление в изменении уровня ряда динамики.
Расчет базисных темпов роста в табл.7 представлен за четырехлетний период. Он показывает некоторый рост выгрузки вагонов по годам. Так, во втором году по сравнению с первым годом реализация возросла на 6,0% , в третьем году - на 10,7% , в четвертом на 11,0%.
Среднегодовой темп роста

Средний темп прироста равен 5,37% и свидетельствует о незначительной тенденции роста.
| Выгрузка вагонов по отделению железной дороги (тыс.усл.ваг.) Таблица 7 | |||||||||
| Месяц | 1 год | 2 год | 3 год | 4 год | квартал | 1 год | 2 год | 3 год | 4 год |
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Январь | 32,10 | 32,80 | 37,30 | 36,30 | I | 95,10 | 98,60 | 111,50 | 103,50 |
| Февраль | 30,00 | 31,90 | 32,20 | 33,20 | |||||
| Март | 33,00 | 33,90 | 42,00 | 34,00 | |||||
| Апрель | 35,80 | 39,50 | 40,90 | 41,90 | II | 99,80 | 111,10 | 114,00 | 121,00 |
| Май | 29,10 | 36,20 | 36,80 | 36,80 | |||||
| Июнь | 34,90 | 35,40 | 36,30 | 42,30 | |||||
| Июль | 31,40 | 32,40 | 35,30 | 34,30 | III | 93,20 | 101,40 | 103,00 | 103,00 |
| Август | 29,30 | 34,30 | 34,00 | 35,00 | |||||
| Сентябрь | 32,50 | 34,70 | 33,70 | 33,70 | |||||
| Октябрь | 35,60 | 34,60 | 34,90 | 36,90 | IV | 111,50 | 112,50 | 113,90 | 116,10 |
| Ноябрь | 35,70 | 36,30 | 35,30 | 35,30 | |||||
| Декабрь | 40,20 | 41,60 | 43,70 | 43,90 | |||||
| Итого: | 399,60 | 423,60 | 442,40 | 443,60 | 399,60 | 423,60 | 442,40 | 443,60 | |
| В среднем | 35,55 | 32,72 | 37,12 | 36,97 | 99,90 | 105,90 | 110,60 | 110,90 | |
| Базисные темпы роста | 100,00 | 106,01 | 110,71 | 111,01 | |||||
Расчет индекса сезонности
Таблица 8
| Периоды | Исходные уровни, тыс. усл. ваг., уi | Скользящие средние, ус | Индекс сезонности, isi | ||
| Год | Квартал | ||||
1 | I. | 95,1 | -- "" -- | ---- | --- |
| II. | 99,8 | (95,1+ 99,8+ 93,2) / 3 = | 96,00 | 1,0392 | |
| III. | 93,2 | (99,8+93,2+111,5) / 3 = | 101,50 | 0,9182 | |
| IV. | 111,5 | и т. д. | 101,10 | 1,1029 | |
2 | I. | 98,6 | -- "" -- | 107,10 | 0,9209 |
| II. | 111,1 | -- "" -- | 103,70 | 1,0714 | |
| III. | 101,4 | -- "" -- | 108,30 | 0,9360 | |
| IV. | 112,5 | -- "" -- | 108,50 | 1,0372 | |
3 | I. | 111,5 | -- "" -- | 112,70 | 0,9896 |
| II. | 114,0 | -- "" -- | 109,50 | 1,0411 | |
| III. | 103,0 | -- "" -- | 110,30 | 0,9338 | |
| IV. | 113,9 | (103+113,9+103,5) / 3 = | 106,80 | 1,0700 | |
|
| I. | 103,5 | (113,9+103,5+121) / 3 = | 112,80 | 0,9200 |
| 4 | II. | 121,0 | (103,5+121+103) / 3 = | 109,17 | 1.1100 |
|
| III. | 103,0 | (121+103+116,1) / 3 = | 113,37 | 0.9100 |
|
| IV. | 116,1 | ------ | ---- | ----- |
2. Данные за каждый квартал используем для расчета индекса сезонности в табл. 8. Скользящие средние определим за каждые три последовательные квартала. Полученное значение скользящей средней относится к середине интервала. При вычислении каждой новой средней исключаем начальный член интервала и присоединяем очередной уровень ряда: первая скользящая средняя у1 = (у1 +у2 + у3): 3;
вторая скользящая средняя у2 = (у2 + у3 + у4): 3 и т. д.
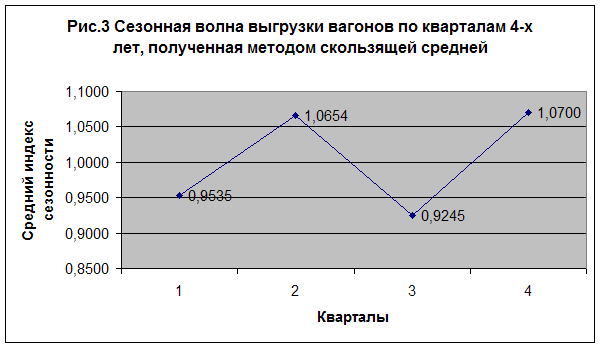
![]() 3. Тенденцию и колебания наглядно показывает график рис.
3 . На оси абсцисс отражается время, на оси ординат – средний индекс сезонности, который рассчитывается за каждый квартал исследуемого периода:
3. Тенденцию и колебания наглядно показывает график рис.
3 . На оси абсцисс отражается время, на оси ординат – средний индекс сезонности, который рассчитывается за каждый квартал исследуемого периода:
Sisi - сумма значений индексов всех одноименных кварталов за весь период,а n - число лет .
Средние индексы для контрольного примера имеют следующие значения:
I квартал = (0,9209 + 0,9896 + 0,9200) : 3 = 0,9535
II квартал = (1,0392 + 1,0714 + 1,0411 + 1,1100) : 4 =1,0654
III квартал = (0,9182 + 0,9360 + 0,9338 + 0,9100) : 4 = 0,9245
IV квартал = (1,1029 + 1,0372 + 1,0700) : 3 = 1,0700
4. График сезонной волны выгрузки вагонов показывает, что наибольший объем работы выполняется ежегодно в четвертом квартале с превышением среднегодового значения на 7,0 % и во втором квартале с ростом объема на 6,54 % над среднегодовым значением.
Задача 5.
ПРАКТИКА ИНДЕКСНОГО МЕТОДА
По данным о продаже товаров на оптовом рынке вычислите:
1) общий индекс цен;
2) общий индекс физического объема товарной массы;
3) общий индекс товарооборота в фактических ценах.
4) покажите взаимосвязь индексов в относительном и абсолютном выражениях.
Расчет выполнен в таблице 9,
Методические указания.
Товарооборот в фактических ценах
Таблица 9
| Товары | Продано товаров в фактических ценах, млн. руб. | Индивидуальный индекс цен, | Товарооборот в сопоставимых ценах, млн. руб. | |
| Базисный период, | Отчетный период, | |||
| 1 | 2 | 3 | 4 | 5 |
| Э. | 200 | 250 | 1,4 | 250:1,4=178,57 |
| И. | 390 | 600 | 1,19 | 600 : 1,19 = 504,2 |
| Н. | 430 | 760 | 1,35 | 760 : 1,35 = 562,96 |
| Итого: | 1020 | 1610 | --- | 1245,73 |
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... распределения генеральной совокупности F(x) и – эмпирической функция распределения Fn(x) , построенной по выборке х1,…,хn, называется функция. Теорема. Если F(x) непрерывна, то распределения статистики Колмогорова Dn не зависит от F(x). Условные математические ожидания и условные распределения. Св-ва условных мат. ожиданий. Аналоги формул полной вероятности и формулы Байеса для мат. ожиданий ГММЕ ...
... дает возможность статистического моделирования, происходящих в населении процессов. Потребность в моделировании возникает в случае невозможности исследования самого объекта. Наибольшее число моделей, применяемых в статистике населения, разработано для характеристики его динамики. Среди них выделяются экспоненциальные и логистические. Особое значение в прогнозе населения на будущие периоды имеют ...
... на задний план традиционными постановками. Несколько лет назад при описании современного этапа развития статистических методов нами были выделены [29] пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять "точек роста": непараметрика, робастность, бутстреп, интервальная статистика, статистика объектов нечисловой природы. Обсудим их. 5. ...










0 комментариев