Навигация
Кольцо многочленов над областью целостности
3. Кольцо многочленов над областью целостности.
Далее будем рассматривать только многочлены с коэффициентами из области целостности K (кольцо без делителей нуля называют областью целостности), т.е. из кольца K, в котором произведение двух элементов может равняться нулю, если только один из сомножителей равен нулю. Это всегда будет подразумеваться, даже если не будет оговорено специально.
При произведении многочленов ![]() степени n и
степени n и ![]() степени m старший член, как следует из формулы (2), равен
степени m старший член, как следует из формулы (2), равен ![]() (это коэффициент при
(это коэффициент при ![]() ). Так как в кольце нет делителей нуля, то
). Так как в кольце нет делителей нуля, то ![]() и, значит,
и, значит, ![]() . Из нашего рассуждения следует также, что
. Из нашего рассуждения следует также, что
![]() .
(6)
.
(6)
Эта формула является уточнением неравенства (5) для случая, когда в кольце K нет делителей нуля. Формула (6) также справедлива и тогда, когда один из многочленов f(x), g(x) или они оба равны нулю. Итак, произведение двух ненулевых многочленов - ненулевой многочлен, поэтому справедлива следующая теорема:
Теорема 1. Кольцо многочленов над областью целостности само является областью целостности.
Данное нами алгебраическое определение многочлена не содержит никакого упоминания о функциях. Тем не менее, с каждым многочленом над областью целостности K можно естественным образом связать функцию, которая определена на K и принимает значения в K.
Пусть ![]() - многочлен с коэффициентами из K. Для любого
- многочлен с коэффициентами из K. Для любого ![]() положим
положим
![]() , (7)
, (7)
где выражение в правой части понимается как результат операций в кольце K. Получаемый при этом элемент ![]() называется значением многочлена f(x) в точке x0. (Слово "точка" употребляется по аналогии со случаем
называется значением многочлена f(x) в точке x0. (Слово "точка" употребляется по аналогии со случаем ![]() , когда x0 можно представлять как точку действительной оси.) Таким образом, каждому элементу x0 кольца K сопоставляется элемент f(x0) того же кольца и тем самым определяется функция на K со значениями в K.
, когда x0 можно представлять как точку действительной оси.) Таким образом, каждому элементу x0 кольца K сопоставляется элемент f(x0) того же кольца и тем самым определяется функция на K со значениями в K.
Покажем, что сложение и умножение многочленов согласуются с обычными операциями, производимыми над функциями, когда складываются или, соответственно, перемножаются значения функций в каждой точке.
Рассмотрим два многочлена: ![]() ,
, ![]() . Пусть h(x) = f(x) + g(x) - их сумма. Докажем, что h(x0)= =f(x0) + g(x0) для любого
. Пусть h(x) = f(x) + g(x) - их сумма. Докажем, что h(x0)= =f(x0) + g(x0) для любого ![]() . В соответствии с формулой (1)
. В соответствии с формулой (1) ![]()
![]() =
= ![]()
![]() , где
, где ![]() , что и требовалось доказать.
, что и требовалось доказать.
Пусть теперь ![]() - произведение многочленов f(x) и g(x). Докажем, что
- произведение многочленов f(x) и g(x). Докажем, что ![]() для любого
для любого ![]() . Перемножим равенства
. Перемножим равенства ![]()
![]() ,
, ![]() . Пользуясь свойствами операций в кольце K (в частности, коммутативностью и ассоциативностью умножения), получим:
. Пользуясь свойствами операций в кольце K (в частности, коммутативностью и ассоциативностью умножения), получим: ![]() , где
, где ![]() . Сравнение полученного результата с формулой (2) позволяет сделать вывод, что
. Сравнение полученного результата с формулой (2) позволяет сделать вывод, что ![]() .
.
Таким образом, функция, определяемая суммой (соответственно произведением) двух многочленов, есть сумма (соответственно произведение) функций, определяемых этими многочленами.
Вообще говоря, соответствие между многочленами и определяемыми ими функциями не является взаимно однозначным. Однако, если кольцо K бесконечно, то различным многочленам из кольца K[x] всегда соответствуют различные функции.
Похожие работы
... об остатках (КТО). Теорема. Пусть – попарно взаимно простые числа, = , , , …, подобраны так, что 1, = , . Тогда решение системы , , будет иметь вид: . Эта теорема лежит в основе метода ортогональных базисов при переводе из системы остаточных классов в позиционную систему счисления. Пусть основания системы остаточных классов ; = = – объем диапазона системы. С выбором системы определяются ее ...
... 4. Бинарные отношения. Математика как наука отражает мир взаимодействующих простых и сложных объектов (вещей, явлений, процессов). Абстрагируясь от реальности, математика рассматривает унарные, бинарные и другие отношения. В вопросе требуется рассмотреть бинарные отношения, их свойства и особо обратить внимание на отношение эквивалентности, заданного на одном множестве. Рассмотрим ...
... -x * y. Полем называется такое ассоциативное коммутативное кольцо с единицей k, в котором всякий ненулевой элемент обратим: . Таким образом, по определению в поле отсутствуют делители нуля. Кольцом называется множество с двумя алгебраическими операциями R (+, *), если: 0. Обратимыми называют те элементы кольца R, которые имеют обратные относительно операции умножения, множество R в данном случае ...
... , работавших в области электротехники, заинтересовалась возможностью создания технологии хранения данных, обеспечивающей более экономное расходование пространства. Одним из них был Клод Элвуд Шеннон, основоположник современной теории информации. Из разработок того времени позже практическое применение нашли алгоритмы сжатия Хаффмана и Шеннона-Фано. А в 1977 г. математики Якоб Зив и Абрахам Лемпел ...
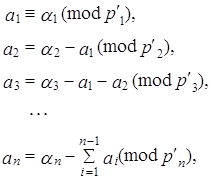
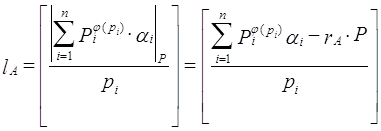
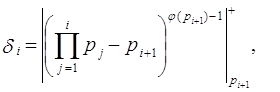
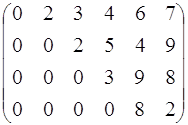
0 комментариев