Навигация
Наименьшее общее кратное
21267
знаков
1
таблица
0
изображений
7. Наименьшее общее кратное.
Наименьшим общим кратным многочленов 
над полем R называется многочлен h, обладающий следующими свойствами: 1) h делится на каждый из многочленов 
, т.е. является их общим кратным; 2) h делит любое общее кратное многочленов .
Теорема Для двух многочленов f и g наименьшее общее кратное [f, g] связано с наибольшим общим делителем (f, g) соотношением
(11)
Доказательство. Для доказательства формулы (23) положим 
, 
, 
, 
и рассмотрим многочлен
(12)
Многочлен 
является общим кратным многочленов f, g и, следовательно, делится на h. Теперь рассмотрим многочлен 
. Равенства 
, 
показывают, что 
- общий делитель многочленов f, g; следовательно, делит d, т.е. 
, где q - некоторый многочлен. Отсюда получаем: 
, т.е. 
. Стало быть, h делится на . Таким образом, h и ассоциированы, т.е. 
, где 
, 
. Из (24) получаем тогда, что 
, что и требовалось доказать.
Из формулы (12) вытекает
Следствие. Наименьшее общее кратное двух взаимно простых многочленов равно их произведению.
8. Сравнения многочленов по многочлену.
Пусть, например, 
- кольцо вычетов по простому модулю p. Два многочлена 
будем называть эквивалентными, если они определяют одну и ту же функцию на 
. Так как в кольце имеется p элементов, то из следствия теоремы 3 непосредственно вытекает следующее утверждение:
Теорема 6. Если многочлены , имеющие степень не выше чем 
, эквивалентны, то они равны.
Определение. Два многочлена 
и 
называются сравнимыми по многочлену 
, если они при делении на дают одинаковые остатки
.
Пример. Многочлены 
и 
сравнимы по многочлену 
, так как они имеют одинаковый остаток при делении это 1.
Теорема 7. Для любых многочленов и :
.
Доказательство. Разделим многочлены и с остатком на :
, 
, 
.
Если , то 
и разность -
делится на . Обратно, если 
, то из равенства
-
следует, что 
. А так как 
, то по свойству отношения делимости в кольце имеем 
, т.е. , или .
Теорема 8. Для многочленов , , 
, 
, 
,
Где 
- любая из операций 
(т.е. сравнения можно почленно складывать, вычитать и перемножать).
Доказательство. Из условия, согласно теореме 7, имеем
-
, -
, т. е. 
, 
.
Складывая, вычитая и перемножая последние равенства, получим:
,
,
.
Отсюда видно, что разность 
делится на при любой операции . Следовательно , 
Теорема 9. Если - общий делитель многочленов и , то
,
т.е. обе части сравнения и многочлен можно делить и умножать на один и тот же многочлен.
Доказательство. Так как - общий делитель многочленов , , то существуют многочлены 
, 
, 
такие, что: 
, 
, 
. Отсюда и из определения делимости многочленов, учитывая отсутствие делителей нуля в кольце, получим:
.
И теперь эта теорема следует непосредственно из теоремы 7.
9. Классы вычетов.
Определение. Класс всех многочленов, сравнимых с многочленом по многочлену , называют классом вычетов по многочлену и обозначают через 
. Множество всех классов вычетов по многочлену обозначим 
Определим на множестве операции сложения и умножения.
Определение. Для любых , 
положим:
+=
, 
=
.
Таким образом, чтобы сложить (перемножить) классы , нужно выбрать из них по одному представителю, сложить (перемножить) их как многочлены и взять класс, содержащий полученный многочлен. В определении в качестве таких представителей выбраны многочлены и . Однако в классах , содержится много других многочленов, и мы заранее не уверены в том, что результат сложения (умножения) классов не зависит от выбора представителей. Если бы результат зависел от выбора представителей, то складывая одни и те же классы, мы могли бы получать разные результаты. Это бы означало, что операции определены некорректно.
Докажем, что определение корректно.
Действительно, пусть, 
, 
. Тогда 
, 
и по теореме 8 имеем:
, 
,
т. е. 
.
Следовательно, результаты операций над классами не зависят от выбора представителей, т. е. операции определены корректно.
Похожие работы
... об остатках (КТО). Теорема. Пусть – попарно взаимно простые числа, = , , , …, подобраны так, что 1, = , . Тогда решение системы , , будет иметь вид: . Эта теорема лежит в основе метода ортогональных базисов при переводе из системы остаточных классов в позиционную систему счисления. Пусть основания системы остаточных классов ; = = – объем диапазона системы. С выбором системы определяются ее ...
... 4. Бинарные отношения. Математика как наука отражает мир взаимодействующих простых и сложных объектов (вещей, явлений, процессов). Абстрагируясь от реальности, математика рассматривает унарные, бинарные и другие отношения. В вопросе требуется рассмотреть бинарные отношения, их свойства и особо обратить внимание на отношение эквивалентности, заданного на одном множестве. Рассмотрим ...
... -x * y. Полем называется такое ассоциативное коммутативное кольцо с единицей k, в котором всякий ненулевой элемент обратим: . Таким образом, по определению в поле отсутствуют делители нуля. Кольцом называется множество с двумя алгебраическими операциями R (+, *), если: 0. Обратимыми называют те элементы кольца R, которые имеют обратные относительно операции умножения, множество R в данном случае ...
... , работавших в области электротехники, заинтересовалась возможностью создания технологии хранения данных, обеспечивающей более экономное расходование пространства. Одним из них был Клод Элвуд Шеннон, основоположник современной теории информации. Из разработок того времени позже практическое применение нашли алгоритмы сжатия Хаффмана и Шеннона-Фано. А в 1977 г. математики Якоб Зив и Абрахам Лемпел ...
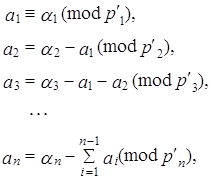
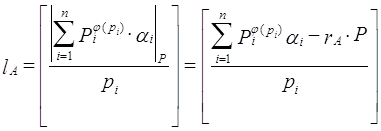
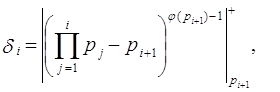
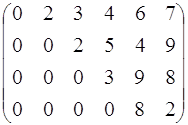
0 комментариев