Навигация
Вычисление наибольшего общего делителя
21267
знаков
1
таблица
0
изображений
6. Вычисление наибольшего общего делителя.
Наибольший общий делитель двух многочленов f и g из кольца R[x] многочленов над полем R может быть найден при помощи алгоритма Евклида. Алгоритм Евклида нахождения наибольшего общего делителя состоит в следующем. Сначала делят с остатком многочлен f на многочлен g, затем многочлен g - на остаток от первого деления, затем остаток от первого деления - на остаток от второго деления и т.д., пока не получится нулевой остаток. Это дает следующую цепочку равенств:
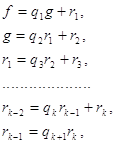(9)
причем 
, поэтому процесс деления конечен. Пусть 
, т.е. f и g принадлежат одному и тому же главному идеалу 
. Поэтому их разность 
, т.е. 
. Аналогично можно доказать, что 
, 
и т.д. Таким образом, 
. Из последнего равенства (21) следует, что 
, тогда 
. Поэтому 
. Следовательно, по теореме 14 
, т.е. 
. Таким образом, последний ненулевой остаток (т.е. rk) и есть наибольший общий делитель многочленов f и g.
Пример. В кольце 
многочленов с действительными коэффициентами найдем наибольший общий делитель многочленов 
, 
. Делим f на g:
Для удобства умножим полученный остаток на 
. При этом последующие остатки также умножатся на некоторые числа, отличные от нуля, что несущественно при нахождении наибольшего общего делителя, так как он находится с точностью до константы. Выполним второе деление:
Полученный остаток разделим на 9 и выполним третье деление:
0
Поскольку остаток равен нулю, то 
.
Наибольший общий делитель нескольких многочленов f1, f2, ..., fm может быть найден индуктивным способом на основании следующей формулы:
. (10)
Для того чтобы найти наибольший общий делитель многочленов 
, следует, согласно этой формуле, найти сначала 
, затем 
и т.д.; 
и будет искомым наибольшим делителем.
Докажем формулу (10). Согласно определению наибольшего общего делителя, делители многочлена 
- это в точности общие делители многочленов 
. Поэтому совокупность всех общих делителей многочленов и fm совпадает с совокупностью всех общих делителей многочленов и fm; отсюда и следует формула (10).
Наибольший общий делитель d двух многочленов 
над полем R, а также всякий многочлен, кратный d, может быть представлен в виде 
, где 
. Такое представление мы называем линейным выражением данного многочлена через многочлены f и g.
Для нахождения линейного выражения наибольшего общего делителя d можно воспользоваться алгоритмом Евклида. В самом деле, первое из равенств (9) дает следующее линейное выражение многочлена r1 через f и g: 
. Подставляя его во второе равенство, получаем линейное выражение многочлена r2: 
. Продолжая так дальше, получаем, в конце концов, линейное выражение наибольшего общего делителя 
.
Пример. Найдем линейное выражение наибольшего общего делителя d многочленов f и g из примера 14.
Результаты делений с остатком, выполненных при решении предыдущего примера, показывают, что 
, 
. Отсюда находим: 
, 
. Таким образом, 
, 
.
Линейное выражение любого многочлена h, кратного d, может быть найдено, исходя из линейного выражения d. А именно: пусть 
и 
. Тогда 
.
На практике линейное выражение многочлена h удобнее искать не с помощью алгоритма Евклида, а методом неопределенных коэффициентов. Запишем искомые многочлены u и v в общем виде с неопределенными (неизвестными) коэффициентами. Приравнивая коэффициенты при одинаковых степенях x в равенстве 
, получим систему уравнений для коэффициентов многочленов u и v. Легко видеть, что эти уравнения будут линейными.
Похожие работы
... об остатках (КТО). Теорема. Пусть – попарно взаимно простые числа, = , , , …, подобраны так, что 1, = , . Тогда решение системы , , будет иметь вид: . Эта теорема лежит в основе метода ортогональных базисов при переводе из системы остаточных классов в позиционную систему счисления. Пусть основания системы остаточных классов ; = = – объем диапазона системы. С выбором системы определяются ее ...
... 4. Бинарные отношения. Математика как наука отражает мир взаимодействующих простых и сложных объектов (вещей, явлений, процессов). Абстрагируясь от реальности, математика рассматривает унарные, бинарные и другие отношения. В вопросе требуется рассмотреть бинарные отношения, их свойства и особо обратить внимание на отношение эквивалентности, заданного на одном множестве. Рассмотрим ...
... -x * y. Полем называется такое ассоциативное коммутативное кольцо с единицей k, в котором всякий ненулевой элемент обратим: . Таким образом, по определению в поле отсутствуют делители нуля. Кольцом называется множество с двумя алгебраическими операциями R (+, *), если: 0. Обратимыми называют те элементы кольца R, которые имеют обратные относительно операции умножения, множество R в данном случае ...
... , работавших в области электротехники, заинтересовалась возможностью создания технологии хранения данных, обеспечивающей более экономное расходование пространства. Одним из них был Клод Элвуд Шеннон, основоположник современной теории информации. Из разработок того времени позже практическое применение нашли алгоритмы сжатия Хаффмана и Шеннона-Фано. А в 1977 г. математики Якоб Зив и Абрахам Лемпел ...
0 комментариев