Навигация
ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ СИММЕТРИЧНОЙ ТРЕХДИАГОНАЛЬНОЙ МАТРИЦЫ
5. ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ СИММЕТРИЧНОЙ ТРЕХДИАГОНАЛЬНОЙ МАТРИЦЫ
Приведя симметричную матрицу к трехдиагональному виду методом Гивенса или Хаусхолдера, необходимо найти ее собственные значения. Чтобы ясней были достоинства трехдиагональной формы, сформулируем задачу о собственных значениях в виде
dеt(А—lE) = 0,
где А — симметричная трехдиагональная матрица. Раcкрыв выражение в скобках, получим
| a1 - l | b2 | 0 | ||
| b1 | a2 - l | = 0 | ||
| bn | ||||
| 0 | bn | an - l |
Произвольный определитель порядка п можно выразить через п миноров порядка п — 1, каждый из которых в свою очередь выражается через п — 1 миноров порядка п — 2. Удобство трехдиагональной формы в том, что на каждом шаге все миноры, кроме двух, оказываются равными нулю. В результате исходный определитель представляется последовательностью полиномов
fm(l) = (am - l) fm-1 (l) – b2 m fm-2(l).
Приняв
f0 (l) = 1 и f1 (l) = a1 - l при r = 2, .... п,
получим совокупность полиномов, известную как последовательность Штурма и обладающую тем свойством, что корни полинома fj (l) располагаются между корнями полинома fj+1 (l). Поэтому для f1 (l) = a1— l можно утверждать, что значение lК = а1 заключено между корнями полинома f2 (l) == (a2 — l) (a1 — l) —b22. Это облегчает итерационное определение корней полинома, так как если известны границы интервалов, в которых лежат значения корней полинома, то их можно найти методом половинного деления. Так последовательно находят корни всех полиномов, и последний из них fn (l) дает все искомые п собственные значения. Эту процедуру можно проиллюстрировать графически (см. рис. 3).
Последовательность Штурма обладает еще и таким свойством: для любого значения b, при котором fn (b) <> 0, число собственных значений матрицы A, больших b, равно числу изменений знака последовательности
1, f1 (b), f2 (b), … , (1)n fn (b).
Если целое число, равное числу изменений знака, обозначить через V(b), то число собственных значений в интервале действительных чисел [b, с] будет равно V(b)—V(c).
| |||
 | |||
| |||
 | |||
| |||
………………………………………………………………………………………………………..
| |||
 | |||
| |||
Рис. 3. Итерационное определение корней полинома
Похожие работы
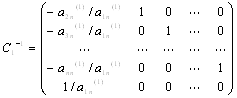
... решения системы. Метод Данилевского Простой и изысканный метод нахождения характеристического многочлена предложил А.М.Данилевский. Рассмотрим идею метода. Рассмотрим матрицу A Для которой находится характеристический многочлен, при помощи подобных преобразований преобразуется к матрице , которая имеет нормальную форму Фробениуса, то есть матрица имеет в явном виде в последнем ...
... , заданного матрицей P= в пространстве R2. Решение. Составим характеристическое уравнение: |P – λ·E|== λ2-5 λ+4=0 Из квадратного уравнения найдем собственные значения линейного оператора λ1=1, λ2=4. Чтобы найти собственные векторы, решим матричные уравнения: (P – λ1 E) X=0 и (P – λ2 E) X=0 В развернутом виде и Соответствующие однородные системы ...
... может быть, четыре или пять, собственных значений. Нахождение всех собственных пар разреженной матрицы представляет собой достаточно сложную вычислительную проблему. Итерационные методы позволяют находить собственные значения и векторы, минуя процедуру построения характеристического полинома. Отличительной чертой этих методов является то, что собственные значения находятся лишь после определения ...
... В.В. О построении собственных значений и функций одной газодинамической задачи Франкеля // Математическое моделирование. 1990. Т. 2. № 10. С. 100-109. Моисеев Е.И. о решении вырождающихся уравнений с помощью биортогональных рядов // Дифференц. уравнения. 1991. Т. 27. № 1. С. 94-103. Мамедов Я.Н. О некоторых задачах на собственные значения для уравнения смешанного типа // Дифференц. уравнения


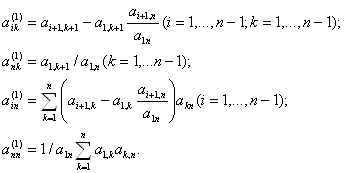


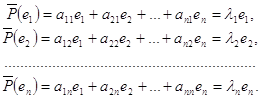
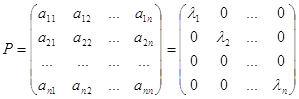


0 комментариев