Навигация
Некоторые свойства многогранника. Задачи о P-медиане
8963
знака
2
таблицы
3
изображения
Г.Г. Забудский, Институт информационных технологий и прикладной математики СО РАН
1. Постановка задачи и определенияЗадачи оптимального размещения объектов имеют много практических приложений. Описываются различные постановки таких задач [1-8]. В данной статье рассматривается известная NP-трудная задача оптимального размещения на графе - задача о p-медиане [1,7-8]. Для ее исследования здесь применяется подход, развиваемый в работах А.А. Колоколова и других [2,4-7,9] для анализа и решения задач целочисленного программирования, основанный на разбиении допустимой области соответствующей непрерывной задачи. В данной работе рассматривается L- разбиение.
Задача о p-медиане сводится к простейшей задаче размещения (ПЗР). Сводимость не гарантирует сохранения некоторых свойств. Например, многогранник ПЗР - квазицелочисленный, а многогранник задачи о p- медиане в общем случае является только связноцелочисленным (квазицелочисленным при p = 1, n-1, где n - число вершин графа) [1].
В работе [2] доказано, что многогранник ПЗР имеет альтернирующую L-структуру. В данной статье показано, что многогранник задачи о p-медиане также имеет альтернирующую L -структуру.
Рассматривается целочисленная модель задачи о p- медиане:
|
| (1) |
где n - количество вершин графа; dij - кратчайшее расстояние между i-й и j- й вершинами графа; p- количество размещаемых объектов. Диагональными будем называть элементы вектора x = (x11,x12,...,xnn) с одинаковыми индексами, а медианными - диагональные, принимающие значение 1. Переменная xij = 1, если вершина j"прикреплена" к вершине i. Условия (4) гарантируют прикрепление только к медианным вершинам. Если условия (5) заменить линейными неравенствами
|
| (2) |
то ограничения (2)-(4),(6) задают многогранник в пространстве размерности n2. Обозначим его через Mp.
Введем определение L-разбиения . Пусть Zk- множество всех k-мерных целочисленных векторов. Тогда L-разбиение непустого множества Rk определим следующим образом:
1) каждая точка zZk образует отдельный класс;
2) нецелочисленные точки x и y эквивалентны, если (x) = (y) и [xi=yi, i =1,...,(x)-1, [x(x)] = [x(x)] , где(x) - номер первой дробной, [a] - наибольшее целое число, не превосходящее a.
В выпуклых множествах с альтернирующим L-разбиением дробныеи целочисленные классы чередуются. В работе [9] предложен критерий альтернируемости L-разбиения:выпуклое замкнутое множество Rk имеет альтернирующее разбиение тогда и только тогда, когда для любого дробного L-класса V существуют целочисленные точки z1,z2 Zk ( называемые окаймляющими) такие, что для любого x V z1j = z2j = xj, j =1,...,(x)-1; z2j = [xj]; j = (x); z1j = ]xj[; j = (x),
где ]a[ - верхняя целая часть числа a. Ясно, что 
знак лексикографического сравнения.
2. Структура L-разбиения
Исследуем структуру L-разбиения многогранника Mp.
ТЕОРЕМА. Для произвольного упорядочения переменных многогранник Mp имеет альтернирующую L-структуру .
Доказательство. Воспользуемся критерием альтернируемости L-структуры. Возьмем произвольный дробный xMp. Обозначим через произвольную перестановку n2 индексов вектора x, т.е. пар чисел от 1 до n. Тогда (i,j) - номер пары (i,j) в перестановке .Рассмотрим два случая.
1. Пусть первая дробная в векторе x Mp - диагональная, т.е. (x) = (i,i) и 
Отметим, что qZ, qp, а тогда q+1 p. Построим вектор z1 Mp Zn2, и 
. Возможны варианты.
1.1. q+1 = p. Для каждого j такого, что найдется kj такой, что 0xkj1 построим множество Jj ={k|xkk = 1}. Покажем, что Jj.
Действительно, пусть нашелся j, для которого Jj=, тогда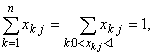 
а так как xkjxkk для любых k и j, имеем 
а из условия 
получаем 0 xij1 и тогда iJj, что противоречит тому, что Jj=.
Вектор z1 строим следующим образом: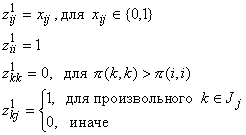 
Нетрудно проверить, что 
.
Похожие работы
... подобраны опорные задачи, которые можно использовать на уроке при изучении данной темы. Таким образом, в данной работе были рассмотрены основные, общие моменты изучения многогранников в школьном курсе стереометрии. В следствие чего дальнейшие исследования могут проходить в направлении более детального изучения отдельных разделов данной темы, а также пропедевтического введения многогранников в ...
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
... V' становится исходным L - классом. Если не существует соседнего дробного L-класса, то либо мы получаем оптимум задачи БП, либо приходим к выводу, что задача не имеет решения. Процесс является конечным, так как M ограничено. Опишем алгоритм перебора L - классов. Для простоты номер итерации будем опускать. Шаг 0. Решаем исходную задачу ЛП. Если она не имеет решения или ее решение целочисленное, ...
... На вспомогательном луче l, проведенном через точку А, построим отрезки АХ1=pe и АС1= qe. Дальнейшие построения сделаны, как в пункте а). Они понятны из рисунка 16, в. Основными способами решения задач построения на изображениях плоских фигур являются: 1. Способ выносных чертежей. 2. Вычислительный способ. 3. Геометрический способ. Задача 4. Параллелограмм АВСD является изображением ...
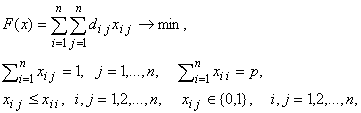
0 комментариев