Навигация
Q+1p. Построим множество JM = {k|xkk = 1}{i}
8963
знака
2
таблицы
3
изображения
1.2 q+1p. Построим множество JM = {k|xkk = 1}{i}.
Ясно, что |JM| p, так как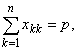 
а 0xii1.
Если |JM| p, то, как рассмотрено выше, строим множества Jj и вектор z1.
Если |JM| p тогда строим множества: D = {ki | 0xkk1}, VN = VM = . Выберем произвольно jD, тогда если найдется такое k, что 0xjk1 и xsk = 0 для всех sVN, то полагаем VM=VM{j}, иначе VN=VN{j}. Вычеркиваем j из D и выбираем следующий элемент из D. Процедура построения множеств VN и VM заканчивается, когда D =. Отметим некоторые свойства множеств VN и VM.
Во-первых, | VM | p-| JM |. Действительно, элемент j включается в множество VM в том случае, если найдется такой элемент k, что 0xjk1 и xsk = 0 для всех sVN. Так как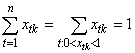 
и xtkxtt, получаем, что 
,откуда 
.
Учитывая, что 
имеем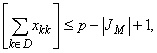 
а тогда |VM| p - |JM|.
Во-вторых, |VN| (p- |JM|)-|VM|. Это следует из того, что |VN|+|VM| = |D|, а |D| = p - |JM| +1 .
В случае, если |VM| p- |JM|, выбираем произвольно (p-|JM|)- |VM| элементов из множества VN и включаем их в множество VM.
Далее для каждого элемента j, такого, что 0xkj1 kj строим множество Jj = {k |k JMVM }
Покажем, что Jj для каждого рассматриваемого j. Действительно, если найдется j, для которого Jj=, тогда рассмотрим множество Dj = {k | 0xkj1}
Получаем, что 0xkk1 для всех kDj, откуда следует, что kVN для всех kDj, т.е. DjVN. Отметим, что элементы множества Dj поочередно включались в множество VN, тогда перед рассмотрением последнего элемента rDj выполнялось условие 0xrj, xsj = 0 для всех sVN, но тогда rVM и, следовательно, Jj. Другими словами, не может быть ситуации, когда все дробные в строке из множества VN. Вектор z1 строится следующим образом: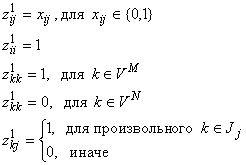 
Для того чтобы закончить рассмотрение случая (x) = (i,i), необходимо показать, как строится вектор z2Mp такой, что 
. В этом случае аналогично строятся множества JM,VN,VM,Jj, Dj с тем изменением, что построение множества VN начинается не с пустого множества, а вначале в него включается элемент {i}. В множество Jj его не включаем. Так как при доказательстве условия Jj мы не пользовались тем, что iJM, оно справедливо и для рассматриваемого случая. Вектор z2 строится аналогично, как расcмотрено выше, за исключением того, что z2ii = 0.
2. Рассмотрим случай, когда (x) = (i,t), it. В отличие от рассматриваемого выше случая при построении вектора z1 не надо строить множество Jt, а положить z1it = 1. Если 0 xii1, то i включаем в VM. При построении вектора z2 не включаем i в множество Jt, если таковое будет строиться.
Теорема доказана.
Отметим, что при построении векторов z1 и z2 мы только некоторым образом округляли дробные компоненты, не меняя значения целочисленных компонент.
СЛЕДСТВИЕ. Для любого дробного решения задачи (1)-(5) подходящим округлением дробных компонент можно построить допустимое решение. Причем по крайней мере одну из дробных компонент можно округлять произвольно.
Доказанное свойство альтернируемости может эффективно использоваться при разработке алгоритмов решения задачи о p-медиане, например, как в [7].
Список литературыЕмеличев В.А., Ковалев М.М., Кравцов М.К. Многогранники, графы, оптимизация. М.: Наука,1981.-344 с.
Заблоцкая О.А. L-разбиение многогранника задачи стандартизации // Моделирование и оптимизация систем сложной структуры. Омск: ОмГУ, 1987. С.151-154.
Забудский Г.Г. Об оценках стоимости связывающей сети в некоторых задачах размещения // Дискретная оптимизация и анализ сложных систем. Новосибирск: ВЦ СО АН СССР, 1989. С. 10 - 25.
Забудский Г.Г. О целочисленной постановке одной задачи размещения объектов на линии // Управляемые системы. Новосибирск, 1990. Т. 30. С.35-45.
Забудский Г.Г. Задачи оптимального размещения взаимосвязанных объектов на линии // Методы решения и анализа задач дискретной оптимизации. Омск: ОмГУ, 1992. С. 5 - 24.
Zabudsky G.G. On the One-Dimensional Space Allocation Problem with Minimal Admissible Distances // Optimization-Based Computer-Aided Modelling and Design.-Prague, Czech Republic: IITA CR. 1995. P. 448-452.
Колоколов А.А., Леванова Т.В. Алгоритмы декомпозиции перебора L-классов для решения некоторых задач размещения // Вест. Омск. ун-та. 1997. N1. С. 21-23.
Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир,1978.-432 с.
Колоколов А.А. Выпуклые множества с альтернирующим L-разбиением // Моделирование и оптимизация систем сложной структуры. Омск: ОмГУ, 1987. С.144-
Похожие работы
... подобраны опорные задачи, которые можно использовать на уроке при изучении данной темы. Таким образом, в данной работе были рассмотрены основные, общие моменты изучения многогранников в школьном курсе стереометрии. В следствие чего дальнейшие исследования могут проходить в направлении более детального изучения отдельных разделов данной темы, а также пропедевтического введения многогранников в ...
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
... V' становится исходным L - классом. Если не существует соседнего дробного L-класса, то либо мы получаем оптимум задачи БП, либо приходим к выводу, что задача не имеет решения. Процесс является конечным, так как M ограничено. Опишем алгоритм перебора L - классов. Для простоты номер итерации будем опускать. Шаг 0. Решаем исходную задачу ЛП. Если она не имеет решения или ее решение целочисленное, ...
... На вспомогательном луче l, проведенном через точку А, построим отрезки АХ1=pe и АС1= qe. Дальнейшие построения сделаны, как в пункте а). Они понятны из рисунка 16, в. Основными способами решения задач построения на изображениях плоских фигур являются: 1. Способ выносных чертежей. 2. Вычислительный способ. 3. Геометрический способ. Задача 4. Параллелограмм АВСD является изображением ...
0 комментариев