Навигация
Влияние структуры ЦФ на шум квантования
4.3. Влияние структуры ЦФ на шум квантования.
Уровень шума квантования зависит от добротности полюсов передаточной функции. Добротность К-ого полюса определяется по формуле
 (4.6)
(4.6)
где rk - радиус полюса, Zk = ![]() (Рис. 4.2, а), Qк = wкТ - угол полюса, wк - частота полюса.
(Рис. 4.2, а), Qк = wкТ - угол полюса, wк - частота полюса.
Действительно, поскольку Z = epT, то
![]()
следовательно
![]()
Отсюда
![]()
поэтому
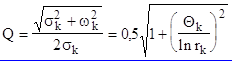
Чем выше добротность полюсов, тем выше уровень шумов квантования поскольку высокой добротности соответствует длительная циркуляция сигнала по цепи ОС при условии медленного снижения уровня сигнала с каждым новым обходом петли обратной связи. Но цепь ОС содержит, как правило, умножители, поэтому с каждой новой циркуляцией по цепи ОС сигнал все больше поражается помехой.
Реализация цепи на каскадном принципе позволяет ослабить негативное воздействие полюсов на помехозащищенность сигнала если, с одной стороны, каждому полюсу подобрать в пару ближайший к нему нуль (при совпадении полюса и нуля влияния полюса на шум полностью исключено), с другой стороны - располагать звенья в порядке нарастания добротности полюсов.
Основой каскадной реализации является представление передаточной функции в виде произведения простейших сомножителей в числителе и знаменателе
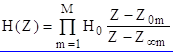 (4.7)
(4.7)
где Z0m - нули H(Z), ZҐm - полюсы H(Z).
Сомножителям 1-го порядка (нули и полюсы - вещественные) соответствуют звенья 1-го порядка, сомножителям 2-го порядка (нули и полюсы - комплексно-сопряженные) соответствуют звенья 2-го порядка. При этом добротность вещественных полюсов тем выше, чем ближе к единичной окружности на плоскости Z располагается полюс.
Пример. Построить цепь на каскадном принципе по известной передаточной функции
H(Z) = 0,8 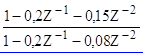
Решение.
Здесь ![]() = 0,1 ± 0,4,
= 0,1 ± 0,4, ![]() = 0,1 ± 0,3
= 0,1 ± 0,3
Следовательно
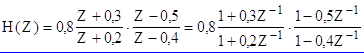
что соответствует схеме цепи на рис. 4.2, б.
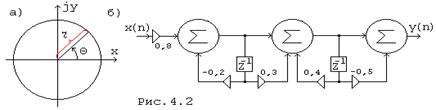
Реализация на каскадном принципе передаточных функций высокого порядка может привести к значительному снижению уровня шумов квантования по сравнению с реализацией другими структурами цепи.
4.4. Квантование коэффициентов. Расчет разрядности.
Габариты, вес и стоимость специализированного процессора, предназначенного для обработки сигналов, тем меньше, чем короче кодовые слова и, в частности, кодовые слова, соответствующие коэффициентам цифровой цепи. Кодовые слова коэффициентов имеют, в общем случае, бесконечную разрядность, поэтому разрядность приходится ограничивать в пределах допусков на отклонение от нормы системных характеристик.
Спецпроцессор функционирует в системе чисел с фиксированной запятой. В этом случае дробная часть кодовых слов определяет модуль числа, целая часть - знак числа: знаку плюс соответствует нуль, знаку минус - единица. Перевод чисел из десятичной системы в двоичную удобно выполнить в форме таблицы, в которой первая клетка отводится исходному числу, остальные клетки - результату перемножения на два дробной части предыдущего числа. Целая часть числа в основных клетках определяет дробную часть двоичного числа.
Пример. Дано десятичное число А(10) = 0,32.
Определить прямой код двоичного числа А(2), если разрядность двоичного числа принять равной 8.
Решение
Заполним таблицу промежуточных расчетов.
| 0,32 2 | 0,64 2 | 1,28 2 | 0,56 2 | 1,12 2 | 0,24 2 | 0,48 2 | 0,96 2 | 1,92 2 | 1,84 |
Отсюда двоичное число А(2) = 0,010100011
Последний - девятый - разряд необходим для округления.
Окончательный результат:
А(2) = 0,01010010 - после округления;
А(2) = 0,01010001 - после усечения.
Оценим погрешность полученных чисел конечной разрядности.
При округлении
А(10)![]() 0*2-1 + 0*2-3 + 1*2-4 + 0*2-5 + 0*2-6 + 1*2-7 + 0*2-8 = 0,3203125
0*2-1 + 0*2-3 + 1*2-4 + 0*2-5 + 0*2-6 + 1*2-7 + 0*2-8 = 0,3203125
Отсюда, относительная погрешность представления исходного числа кодовым словом конечной разрядности равной 8 составляет d » 0,1 %
При усечении
А(10)![]() 0*2-1 + 0*2-3 + 1*2-4 + 0*2-5 + 0*2-6 + 0*2-7 + 1*2-8 = 0,31640625
0*2-1 + 0*2-3 + 1*2-4 + 0*2-5 + 0*2-6 + 0*2-7 + 1*2-8 = 0,31640625
что соответствует d » 1,15 %
Существуют различные способы расчета разрядности коэффициентов по допускам на системные характеристики. Самый простой способ - метод проб.
Расчет по методу проб начинается с выбора разрядности коэффициентов ориентировочно, субъективно. Затем следует расчет системных характеристик с новыми - приближенными - значениями коэффициентов, оценка искажений характеристик и соответствующая коррекция разрядности коэффициентов в ту или иную сторону. Расчет повторяется столько раз, сколько потребуется для удовлетворительного решения задачи по выбору разрядности коэффициентов.
Похожие работы
... Студент группы 220352 Чернышёв Д. А. Справка— отчет о патентном и научно- техническом исследовании Тема выпускной квалификационной работы: телевизионный приёмник с цифровой обработкой сигналов. Начало поиска 2. 02. 99. Окончание поиска 25.03.99 Предмет поиска Страна, Индекс (МКИ, НКИ) № ...
... 1 – «-» Причем 1-ый разряд слева – знаковый разряд. 16 14 12 10 8 6 4 2 Т 2Т 2. Связи между аналоговыми и дискретными сигналами. При обработке сигнала на ЭВМ необходимо в максимальной степени, чтобы дискретный или цифровой сигнал содержал все признаки аналогового сигнала. При дискретизации возможна потеря информации, которая ...
... примерно 6%. В общем, в районе 1 - 4 кГц чувствительность уха по всем параметрам максимальна, и составляет не так уж и много, если брать не логарифмированные значения, с которыми приходится работать цифровой технике. Примите на заметку - многое из того, что происходит в цифровой обработке звука, может выглядеть ужасно в цифрах, и при этом звучать неотличимо от оригинала. В цифровой обработке ...
... несущими и амплитудно-фазовая модуляция с одной боковой полосой (АФМ-ОБП). 3. Выбор длительности и количества элементарных сигналов, используемых для формирования выходного сигнала В реальных каналах связи для передачи сигналов по частотно ограниченному каналу используется сигнал вида , но он бесконечен во времени, поэтому его сглаживают по косинусоидальному закону. , где - ...
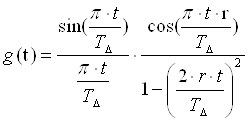
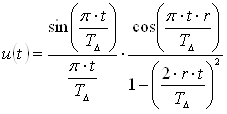
0 комментариев