Преобразование Фурье и Лапласа для дискретных сигналов
Теорема энергий (равенство Парсеваля)
Дискретные цепи
Общие свойства передаточной функции
Круговая свёртка
Расчёт энергии сигнала в дискретной цепи
Метод перекрытия с суммированием
Расчёт нерекурсивных ЦФ общего вида
Антисимметричные фильтры
Метод частотной выборки
Схема фильтра с вещественными отводами
Эффекты конечной разрядности и их учет
Влияние структуры ЦФ на шум квантования
Чувствительность
Расчет по условию ограничения максимума сигнала
Восстановление непрерывного сигнала
Навигация
Дискретные цепи
Цифровая обработка сигналов
72858
знаков
1
таблица
34
изображения
2. Дискретные цепи.
2.1 Разностное уравнение и дискретная цепь.
Непрерывный сигнал на входе линейной системы x(t) и соответствующий сигнал y(t) на выходе связаны дифференциальным уравнением. Замена непрерывной переменной t на дискретную переменную nT приводит к замене дифференциального уравнения разностным уравнением. Каноническая форма разностного уравнения общего вида, учитывающая в явном виде наличие в системе как прямых, так и обратных связей, запишется так
y(nT) =
am x(nT - mT) +
y(nT -
), (2.1)
где (M + 1) - число прямых связей,
Z - число обратных связей,
m, 
, n - целые положительные числа.
Аналитические методы решения разностных уравнений во многом повторяют методы решения дифференциальных уравнений и позволяют получить решение в общем виде, пригодном для анализа работы дискретной системы. Численные методы решения приводят к результату в виде числовой последовательности, поэтому разностное уравнение в этом случае воспринимается как алгоритм функционирования дискретной системы, пригодной для программирования на ЭВМ работы такой системы.
Система работа которой описывается разностными уравнениями, является дискретной так как она способна воздействовать только на отсчеты сигнала. Дискретная система и дискретная цепь осуществляет, согласно (2.1) следующие операции над дискретными сигналами.
1. Сдвиг (запаздывание) на целое число интервалов T
2. Умножение на некоторый коэффициент am или b
3. Сложение сигналов.
Перечисленные операции образуют полный базис, в котором можно реализовать заданное воздействие на сигнал.
Набору операций базиса соответствует набор типов элементов дискретной цепи : элементы памяти (задержки), умножители и сумматоры.
Каноническая схема дискретной цепи общего вида, соответствующая разностному уравнению (2.1), приведена на Рис. 2.1.
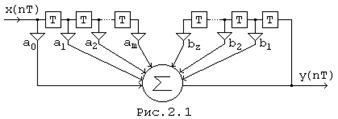
Разностное уравнение с постоянными коэффициентами am , b
описывает линейную дискретную цепь. Разностное уравнение с коэффициентами, зависящими от уровня отсчетов дискретного сигнала, описывает нелинейную дискретную цепь.
Разностное уравнение составляется непосредственно по схеме цепи, учитывая возможные пути прохождения сигнала, или по системным характеристикам цепи.
Пример. Составить разностное уравнение цепи, схема которой приведена на Рис. 2.2, а.
Решение.
Здесь имеется три пути прохождения сигнала от входа до выхода цепи, по которым сигналы проходят и затем складываются в сумматоре. Поэтому разностное уравнение имеет вид
y(nT) = 0,5 x(nT) - 0,7 x(nT - T) + 0,35 x(nT - 2T).
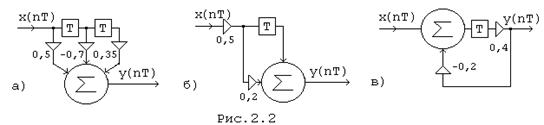
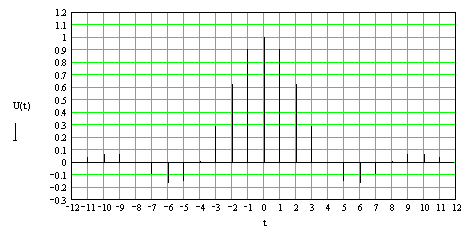
Пример. Определить y(nT) (Рис. 2.2, б), если x(nT) = {1,0 ; 0,5}.
Решение.
Разностное уравнение цепи y(nT) = 0,5 x(nT - T) + 0,1 x(nT) численное решение разностного уравнения :
n=0; y (0T) = 0,5 x(-T) + 0,1 x(0T) = 0,1;
n=1; y (1T) = 0,5 x(0T) + 0,1 x(1T) = 0,55;
n=2; y (2T) = 0,5 x(1T) + 0,1 x(2T) = 0,25;
n=3; y (3T) = 0,5 x(2T) + 0,1 x(3T) = 0.
Следовательно y(nT) = {0,1; 0,55; 0,25}.
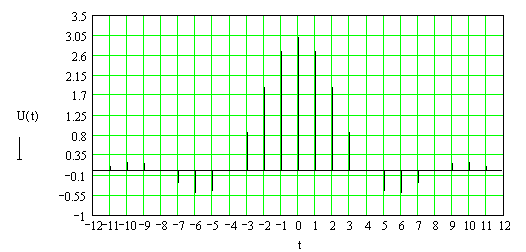
Графики сигналов x(nT) и y(nT) приведены на рис (2.3,а,б).
Пример. Определить сигнал на выходе цепи (рис 2.2,в), если y(nT)={0,1; 0,1}.
Решение.
Цепь содержит обратную связь (ОС), поэтому сигнал на выходе цепи формируется как сигнал со стороны входа, так и со стороны выхода.
y(nT) = 0,4 x(nT-T) - 0,08 y(nT-T)
n=0 y(0T) = 0,4 x(-T) - 0,08 y(-T) = 0
n=1 y(1T) = 0,4 x(0T) - 0,08 y(0T) = 0,4
n=2 y(0T) = 0,4 x(1T) - 0,08 y(1T) = 0,368 и т.д. ...
Следовательно y(nT) = {0; 0,4; 0,368; ...}.
В данном случае за счет циркуляции сигнала по цепи ОС выходной сигнал состоит из бесконечного числа отсчетов.
Дискретная цепь, содержащая ОС, называется рекурсивной. Дискретная цепь без ОС называется нерекурсивной.
2.2 Передаточная функция дискретной цепи.
Замена сигналов в разностном уравнении (2.1) на Z - изображения этих сигналов
, 
приводит к алгебраизации разностного уравнения
.
Алгебраизация осуществляется применением теорем линейности и запаздывания.
Переход в область Z - изображений позволяет ввести понятие передаточной функции дискретной цепи H(Z), которая определяется как отношение Z - изображения сигнала на выходе цепи к Z - изображению сигнала на входе цепи. Поэтому, учитывая алгебраическую форму разностного уравнения общего вида, можно записать общий вид передаточной функции дискретной цепи
.
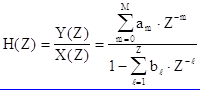(2.3)
Отсюда, в частности, для нерекурсивной цепи
.
(2.4)
Если нерекурсивная цепь состоит всего из одного элемента запаздывания, то 
,
что находит своё отражение в обозначении элементов памяти на схемах дискретных цепей.
Передаточная функция конкретной цепи формируется по передаточным функциям её элементов согласно общих правил линейных цепей. В частности, для цепи содержащей ОС применяется известная формула
, (2.5)
где 
-
передаточная функция цепи
прямого прохождения сигнала,
-
предаточная функция цепи ОС.
Пример. Оперделить передаточную функцию цепи на рис. (2.4,а).
Решение.
,
где 
, 
.
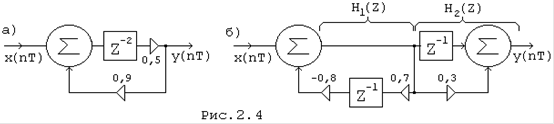
Пример. Определить передаточную функцию на рис.(2.4,б).
Решение.
,
где 
- передаточная функция рекурсивной части схемы,
- передаточная функция нерекурсивной части цепи.
По известной передаточной функции можно легко определить разностное уравнение цепи.
Пример. Составить разностное уравнение цепи на рис.(2.2,в).
Решение.
Здесь 
.
Поэтому
.
Отсюда 
.
Следовательно переходя к оригиналам: y(nT)= 0,4 x(nT-T) - 0,08 y(nT-T).
Похожие работы
... Студент группы 220352 Чернышёв Д. А. Справка— отчет о патентном и научно- техническом исследовании Тема выпускной квалификационной работы: телевизионный приёмник с цифровой обработкой сигналов. Начало поиска 2. 02. 99. Окончание поиска 25.03.99 Предмет поиска Страна, Индекс (МКИ, НКИ) № ...
... 1 – «-» Причем 1-ый разряд слева – знаковый разряд. 16 14 12 10 8 6 4 2 Т 2Т 2. Связи между аналоговыми и дискретными сигналами. При обработке сигнала на ЭВМ необходимо в максимальной степени, чтобы дискретный или цифровой сигнал содержал все признаки аналогового сигнала. При дискретизации возможна потеря информации, которая ...
... примерно 6%. В общем, в районе 1 - 4 кГц чувствительность уха по всем параметрам максимальна, и составляет не так уж и много, если брать не логарифмированные значения, с которыми приходится работать цифровой технике. Примите на заметку - многое из того, что происходит в цифровой обработке звука, может выглядеть ужасно в цифрах, и при этом звучать неотличимо от оригинала. В цифровой обработке ...
... несущими и амплитудно-фазовая модуляция с одной боковой полосой (АФМ-ОБП). 3. Выбор длительности и количества элементарных сигналов, используемых для формирования выходного сигнала В реальных каналах связи для передачи сигналов по частотно ограниченному каналу используется сигнал вида , но он бесконечен во времени, поэтому его сглаживают по косинусоидальному закону. , где - ...
0 комментариев