Навигация
Целая и дробная части действительного числа
7095
знаков
0
таблиц
3
изображения
Т.С. Кармакова , доцент кафедры алгебры ХГПУ
В различных вопросах теории чисел, математического анализа, теории рекурсивных функций и в других вопросах математики используются понятия целой и дробной частей действительного числа.
В программу школ и классов с углубленным изучением математики включены вопросы, связанные с этими понятиями, но на их изложение в учебнике алгебры для 9 класса [1] отведено всего 34 строки. Рассмотрим более подробно эту тему.
Определение 1
Целой частью действительного числа х называется наибольшее целое число, не превосходящее х.
Целая часть числа обозначается символом [х ] и читается так: “целая часть х” или: “целая часть от х ”. Иногда целая часть числа обозначается Е(х) и читается так: “антье х ” или “ антье от х ”. Второе название происходит от французского слова entiere – целый.
Пример.
Вычислить [x], если х принимает значения:
1,5; 3; -1.3; -4.
Решение
Из определения [x] следует:
[1,5] = 1, т.к. 1
Z, 1 
1,5
[ 3 ] = 3, т.к. 3Z, 3 3
[-1,3]=-2, т.к. –2Z, -2 -1,3
[-4] =-4, т.к. -4Z, -4-4.
Свойства целой части действительного числа.
1°. [ x ] = x , если хZ
2°. [ x ] x [ x ] + 1
3°. [ x + m ] = [ x ] + m , где m Z
Рассмотрим примеры использования этого понятия в различных задачах.
Пример 1
Решить уравнения:
1.1[ x ] = 3
[ x + 1,3 ] = - 5
[ x + 1 ] + [ x – 2] – [x + 3 ] = 5
1.4 [ x ]
- 7 [ x ] + 10 = 0
Решение
1.1 [ x ] = 3. По свойству 2° данное уравнение равносильно неравенству 3 х 4
Ответ : [ 3 ; 4 )
[ x + 1,3 ] = - 5. По свойству 2° :
- 5 х + 1,3 - 4 
- 6,3 х - 5,3
Ответ : [ -6,3 ; -5,3 )
[ x + 1 ] + [ x – 2 ] – [ x + 3 ] = 5. По свойству 3°:
[ x ] + 1 + [ x ] – 2 – [ x ] – 3 = 5
[ x ] = 9 9 x 10 (по 2° )
Ответ : [ 9 ; 10 )
1.4 [ x ]- 7 [ x ] + 10 = 0 Пусть [ x ] = t , тогда t - 7 t + 10 = 0 
, т.е.
Ответ : [ 2 ; 3 ) 
[ 5 ; 6)
Пример 2.
Решить неравенства:
2.1 [ x ] 
2
[ x ] > 2
[ x ] 2
[ x ] < 2
[ x ] - 8 [ x ] + 15 0
Решение
2.1 Согласно определению [ x ] и 1°, этому неравенству удовлетворяют х
Ответ : [ 2 ; 
).
2.2 Решение этого неравенства: х
.
Ответ : [ 3 ; ).
Похожие работы
... мест. Методы Коши получили всеобщее распрастранение, применялись оттачивались весь XIX век. Идеи и методы Коши плодотворно пользуются и обобщаются современными математиками и сегодня. 4 Создание теории действительного числа После «наведения порядка» в математическом анализе встал вопрос о ситуации в арифметике. «К необходимости разработки теории действительных чисел приводили многие задачи ...
... что если уравнение (25) имеет хотя бы одно решение, то оно имеет их бесчисленное множество. Нельзя, конечно, утверждать, что формулами (31) даются все решения уравнения (25). В теории алгебраических чисел доказывается, что все решения уравнения (25) в целых числах можно получить, взяв некоторое конечное и определенное зависящее от и число решений этого уравнения и размножив их с помощью формул ...
... случаи? Как записать формулу решения в виде дроби? При этом можно рассмотреть и сокращение дроби, когда числитель и знаменатель представляют произведение. Перейдем теперь к изложению той методики преподавания умножения на дробь, которая получила в настоящее время признание в педагогической практике и в учебно-методической литературе. Можно подвести учащихся к новому определению умножения путем ...
... , сколько времени потребуется для его составления, как много места для возможных ошибок? Естественно, об этом задумывались и авторы языков программирования. Поэтому во всех существующих языках имеются типы переменных, отвечающие за хранение больших массивов данных. В языке Паскаль они так и называются: "массивы". Массивом будем называть упорядоченную последовательность данных одного типа, ...
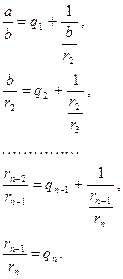
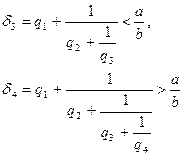
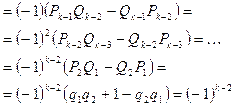
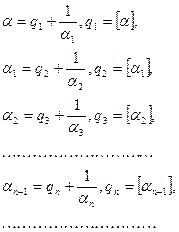
0 комментариев