Распределение примесей после диффузии

1.3. Распределение примесей после диффузии.

Основой математического описания процессов диффузии являются два дифференциальных уравнения Фика (немецкий ученый A. Fick предложил их в 1855 г.).

Первое уравнение (первый закон Фика) записывается следующим образом:

J = - D grad N (7)

где J - плотность потока диффундирующего вещества, т.е. количество вещества, проходящего за единицу времени через единичную площадь поверхности, перпендикулярной направлению переноса вещества;

N - концентрация атомов примеси.

D - коэффициент диффузии.

Физический смысл этого уравнения — первопричиной диффузионного массопереноса вещества является градиент его концентрации. Скорость переноса пропорциональна градиенту концентрации, а в качестве коэффициента пропорциональности вводится коэффициент диффузии. Знак минус в правой части (7) указывает на то, что диффузия происходит в направлении убывания концентрации. Другими словами, диффузия идет благодаря стремлению системы достичь физико-химического равновесия. Процесс будет продолжаться до тех пор, пока химические потенциалы компонентов всей системы не станут равными. Уравнение (7) описывает стационарный (установившийся) процесс - процесс, параметры которого не зависят от времени.

В макроскопическом представлении коэффициент диффузии определяет плотность потока вещества при единичном градиенте концентрации и является, таким образом, мерой скорости выравнивания градиента концентрации. Размерность коэффициента диффузии - м²/с. В общем случае диффузия анизотропна и коэффициент диффузии - симметричный тензор второго ранга.

Согласно микроскопическому определению, компонента D_x коэффициента диффузии D по координате x связана со среднеквадратичным смещением диффундирующих атомов по координате x и интервалом времени t, в течение которого это смещение произошло соотношением

Когда концентрация вещества изменяется только в одном направлении (одномерная диффузия) и при диффузии в изотропной среде (коэффициент диффузии - скаляр) первое уравнения Фика имеет следующий вид:

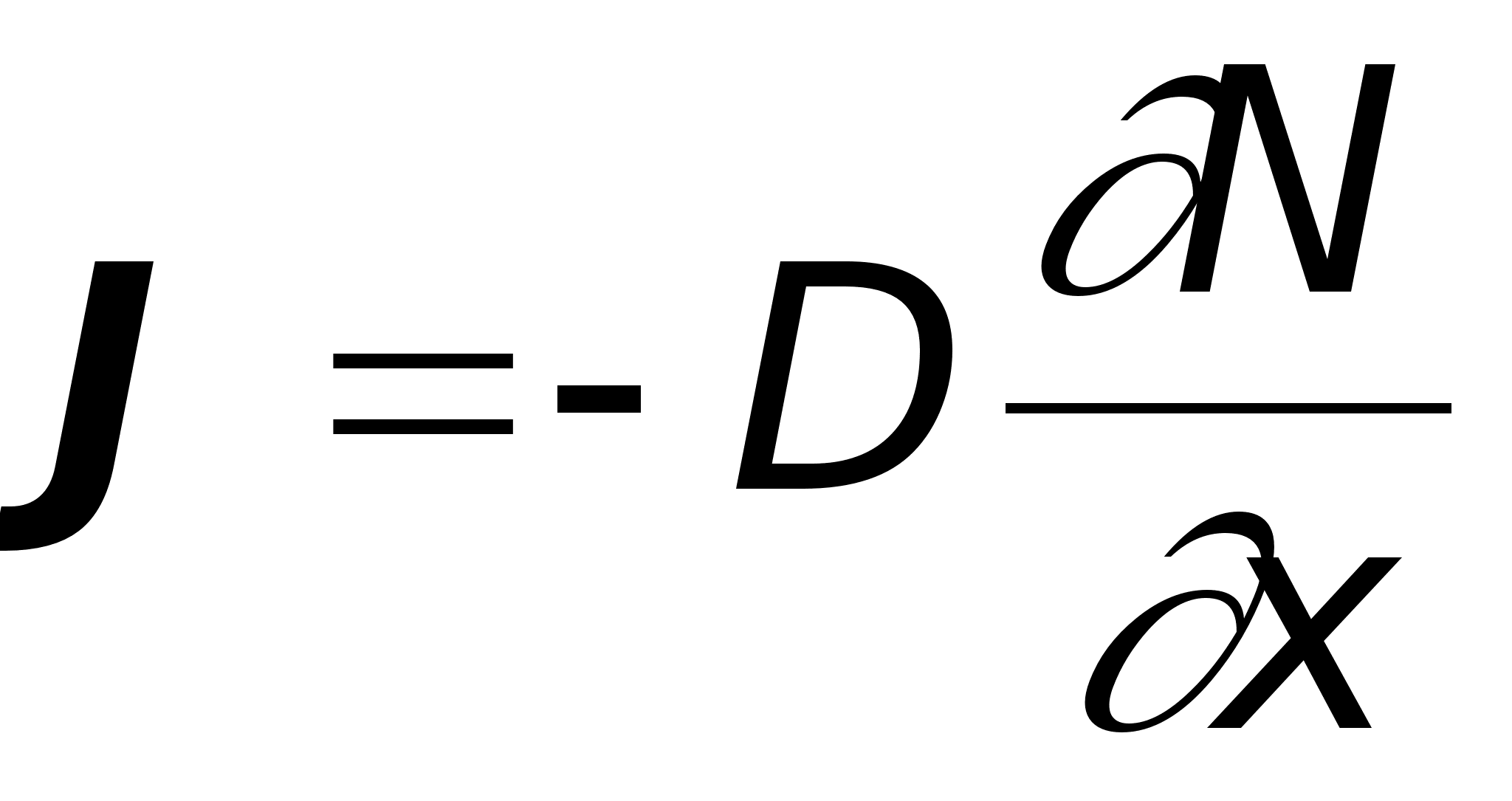
(8)

При простейшем анализе структур и в простейших моделях процессов легирования в технологии изготовления ИМС предполагаются именно такие условия диффузии.

Второе уравнение диффузии (второй закон Фика) получается путем сочетания первого закона и принципа сохранения вещества, согласно которому изменение концентрации вещества в данном объеме должно быть равно разности потоков этого вещества на входе в объем и выходе из него.

В общем случае второе уравнение диффузии имеет следующий вид

(9)

Для одномерной диффузии в изотропной среде уравнение (9) можно записать

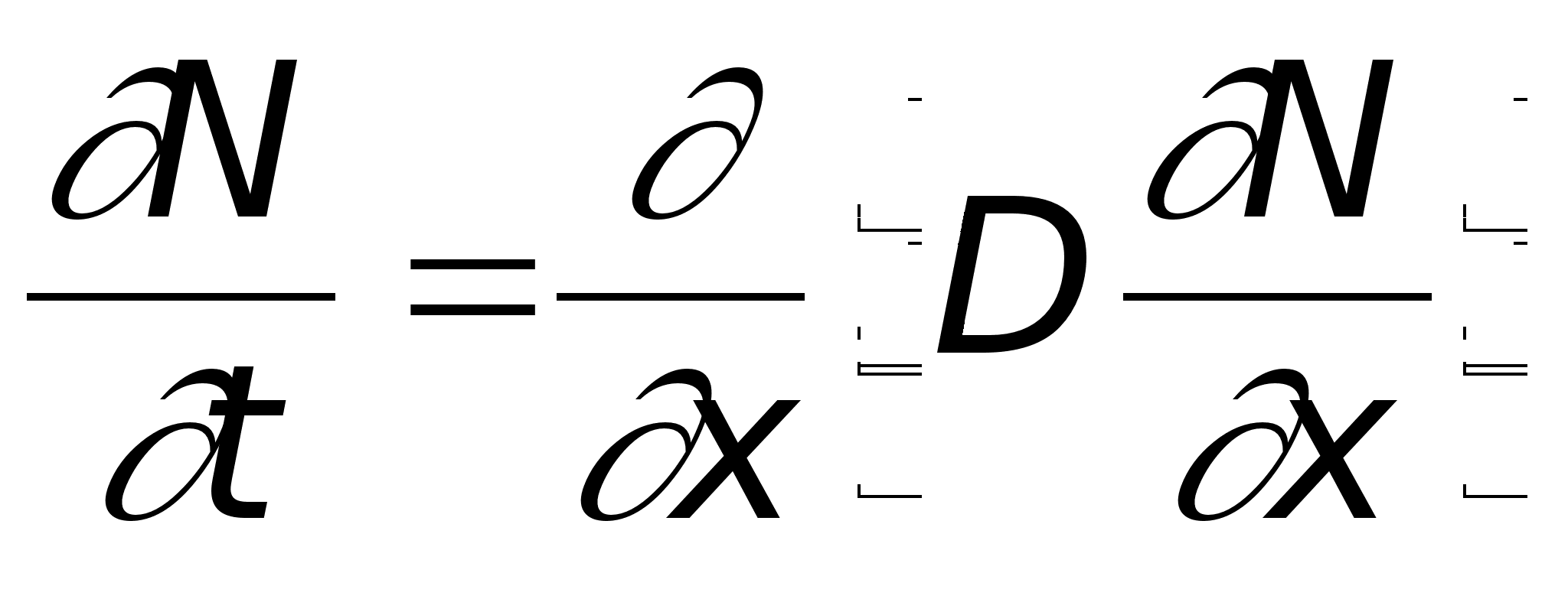(10)

Второй закон Фика характеризует процесс изменения концентрации диффундирующей примеси во времени в различных точках среды и является математической моделью нестационарного (развивающегося) состояния системы (описывает период времени от начала процесса до установления стационарного состояния).

При постоянстве коэффициента диффузии D (независимости его от концентрации примеси) уравнение (10) упрощается

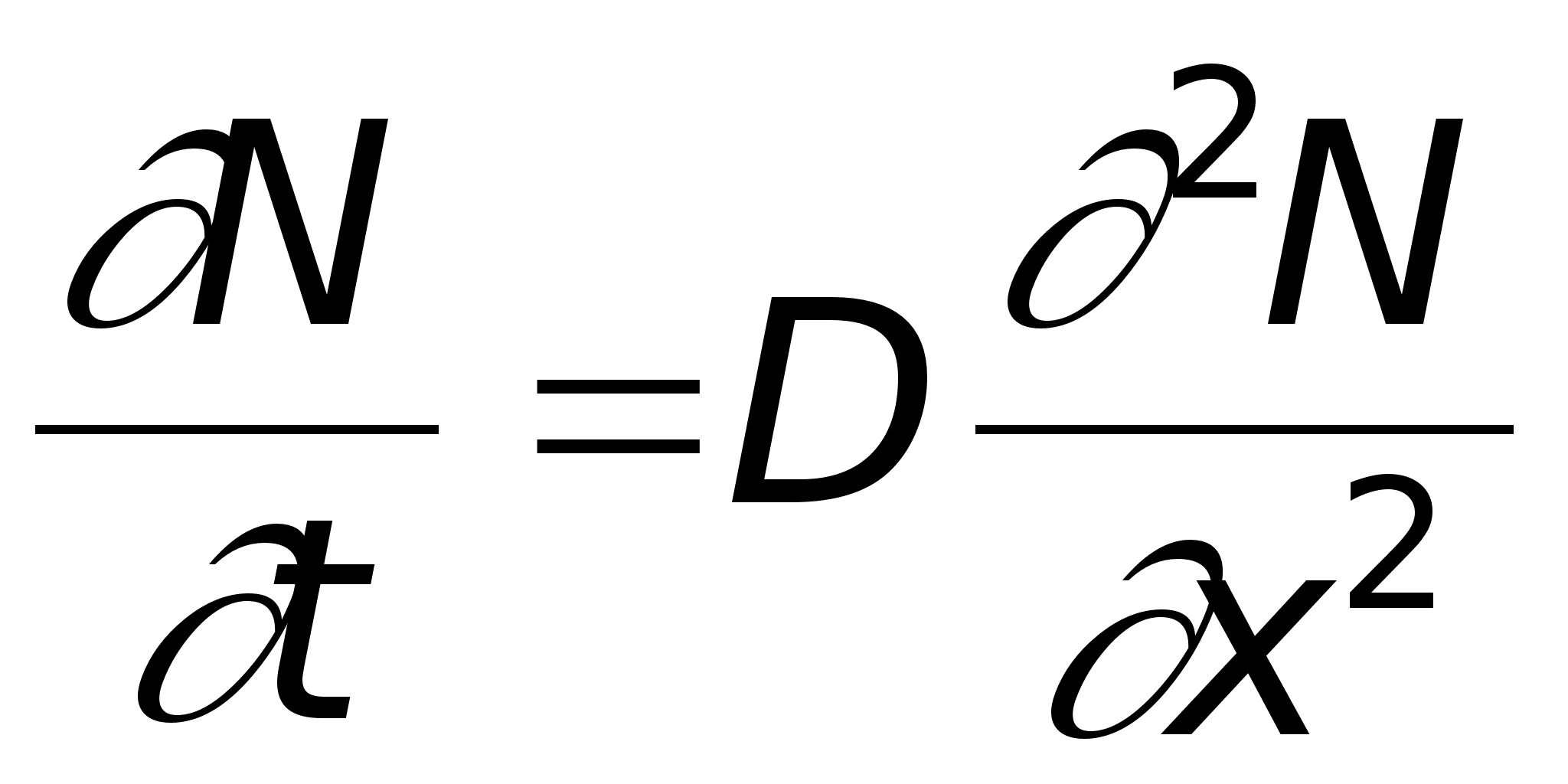(11)

Допущение о постоянстве коэффициента диффузии справедливо в большом количестве случаев, анализируемых в технологии ИМС.

Уравнения диффузии являются чисто феноменологическими, т.е. они не содержат никаких сведений о механизмах диффузии - о диффузионном процессе на атомном, уровне. Кроме того, уравнения (7) - (11) не содержат информации о зарядовом состоянии диффундирующих частиц.

Процессы диффузии, используемые для изготовления интегральных структур, обычно анализируются с помощью частных решений уравнения (11) т.к., в отличие от (8), именно оно содержит важный параметр - время установления некоторого анализируемого состояния системы. Основная цель решения уравнения - найти распределение примеси N(x,t) в полупроводнике после диффузии в течение определенного времени t при различных условиях осуществления процесса.

Общее решение уравнения (11) для бесконечного твердого тела при заданном в общем, виде начальном распределении примеси N(x,0) = f(x) может быть найдено методом разделения переменных. Оно имеет вид

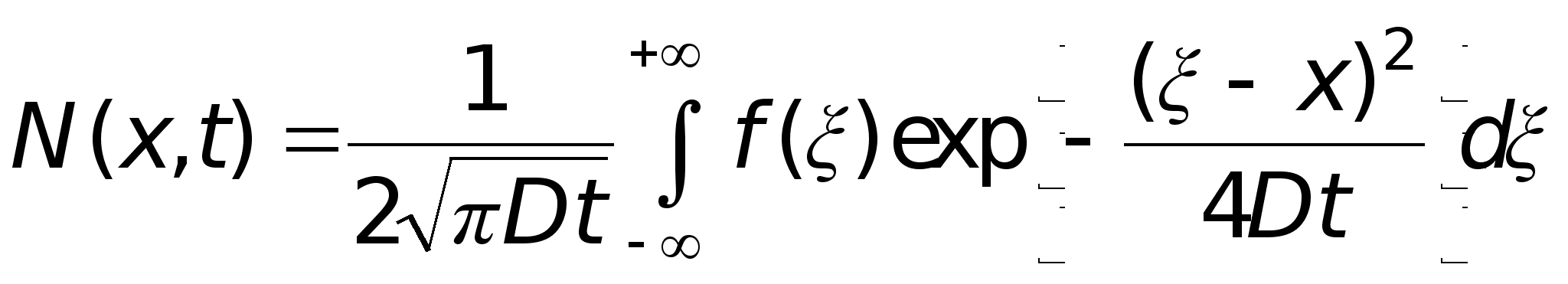, (12)

здесь текущая координата интегрирования.

Бесконечным в одномерном представлении называют тело, простирающееся от x=0 до x=-и до x=+ .

Часто при поиске распределения концентрации примеси в полупроводнике необходимо решение уравнения (11) для полубесконечного твердого тела. Полубесконечным в одномерном представлении называют тело, простирающееся от x=0 до x=+ .

Для этого случая выражение (12) может быть приведено к виду

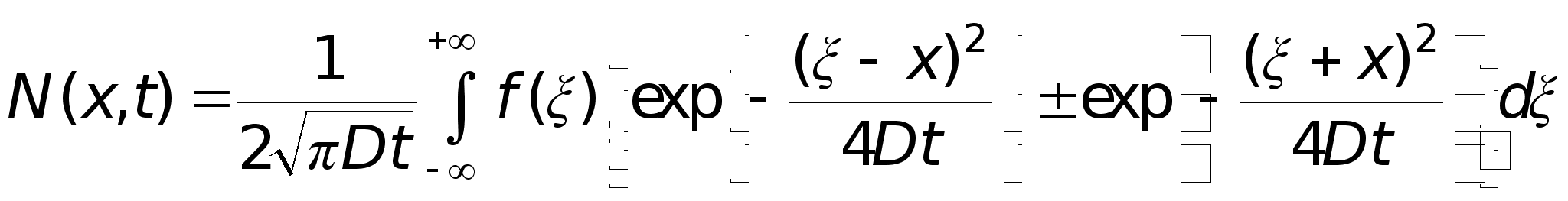(13)

В выражении (13) знак плюс относится к ситуации, когда граница твердого тела (x=0) является непроницаемой для диффундирующего вещества, находящегося в области x>0, (отражающая граница), а знак минус - к случаю, когда на границе твердого тела в любой момент времени концентрация диффундирующего вещества, также находящегося в области x>0, равна нулю - связывающая граница.

Представленные решения позволяют находить распределения примеси в твердом теле при любых начальных условиях. Решение конкретной задачи сводится к подстановке в (12) или (13) соответствующих ситуации начальных условий с последующими, как правило, очень громоздкими преобразованиями.

Похожие работы

Общая и неорганическая химия

Скачать

442397

6

13

... с кислородом, восстановлением - отнятие кислорода. С введением в химию электронных представлений понятие окислительно-восстановительных реакций было распространено на реакции, в которых кислород не участвует. В неорганической химии окислительно-восстановительные реакции (ОВР) формально могут рассматриваться как перемещение электронов от атома одного реагента (восстановителя) к атому другого ( ...

Термическое отделение для непрерывного отжига металла

Скачать

124763

28

4

... 3. РАСЧЕТ ОБОРУДОВАНИЯ И ПРОЕКТИРОВАНИЕ ОТДЕЛЕНИЯ   3.1 Технико-экономическое обоснование основного, дополнительного и вспомогательного оборудования Основным оборудованием термического отделения для термообработки холоднокатаного листа является агрегат непрерывного отжига. Печная часть агрегата включает многокамерную башенную печь отжига, установки и камеры ускоренного перестаривания и ...

Технология производства полупроводниковых материалов типа А2В6

Скачать

75661

4

1

... компонентов над распла­вами соединений составляют от двух до нескольких десятков атмосфер; температура плавления большинства соединений пре­вышает 1200° С. 1.3.Получение полупроводниковых монокристаллов соединений типа АIIBVI. Рассмотрев выше изложенные методы можно добавить , что не все соединения типа AIIBVI можно получить одним и тем ...

Керамика, сварка

Скачать

59910

17

11

... которого расположены стержни, перемещающие вверх измельчаемый материал и шары. Конусная дробилка. Шаровая дробилка Для окисной высококачественной керамики используют более экономически выгодный химический метод получения керамических порошков - метод одновременного осаждения нерастворимых осадков. ...