Навигация
Распределение примеси при диффузии из слоя конечной толщины (диффузия из ограниченного источника) в полубесконечное тело с отражающей границей
1.3.3 Распределение примеси при диффузии из слоя конечной толщины (диффузия из ограниченного источника) в полубесконечное тело с отражающей границей.
Диффундирующая примесь поступает в полубесконечное тело из источника, который представляет собой примыкающий к границе тела слой толщиной h, примесь в котором распределена равномерно. Такой источник называют ограниченным. Концентрация примеси в источнике - No. Полагается, что в принимающем диффузант твердом теле нет рассматриваемой примеси.
При абсолютно непроницаемой для диффузанта (отражающей) границе поток примеси через поверхность x=0 должен обращаться в нуль при всех t0
 для t0 (24)
для t0 (24)
Начальное распределение концентраций для рассматриваемого случая задаётся в виде
N(x,0) = Noдля 0xh
N(x,0) = 0 для x>h
Граничным
условием является,
определяемое
условием (24),
постоянство
количества
примеси в источнике
и полупроводнике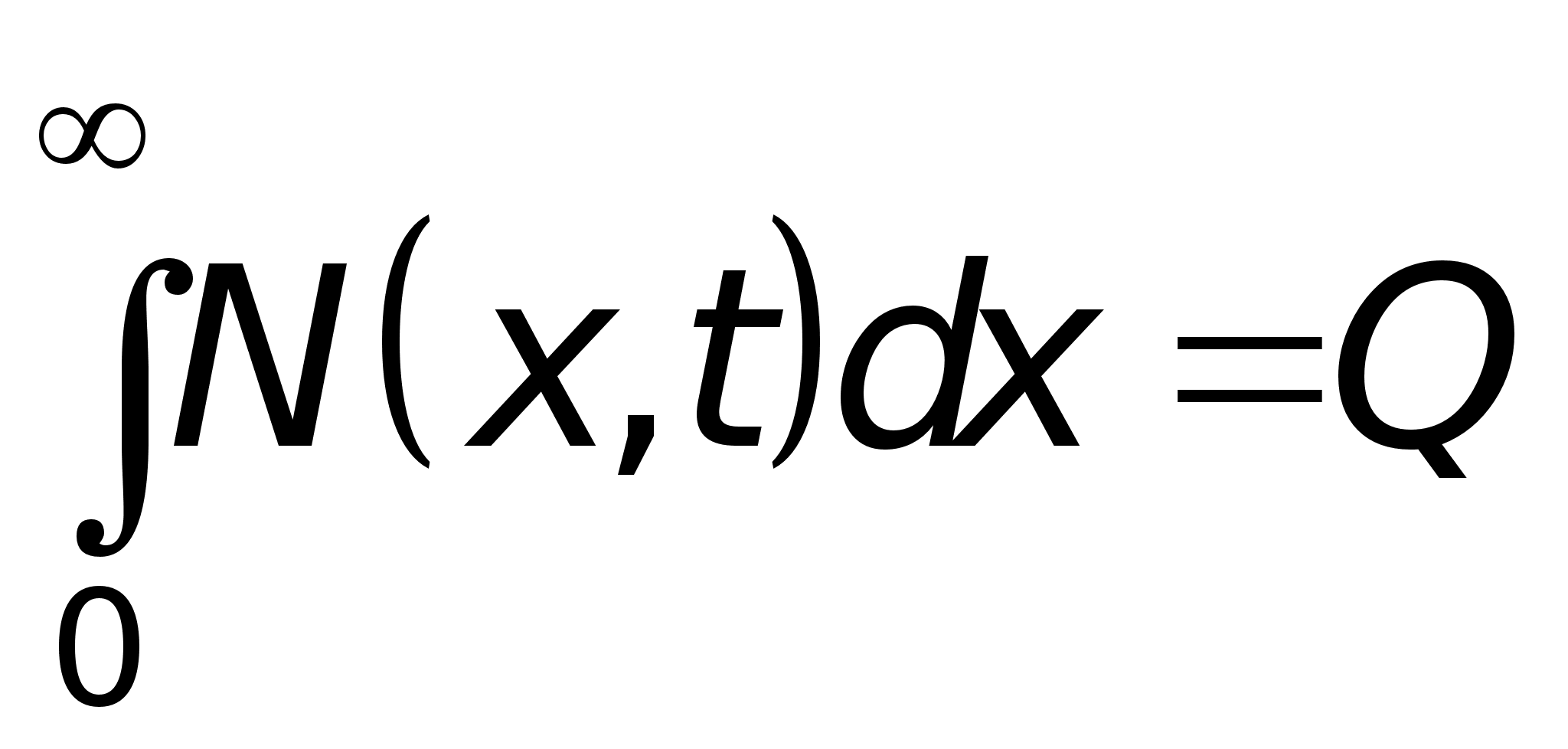
Для реализации начального распределения такого типа диффундирующая примесь должна быть введена в твердое тело до начала диффузии.
Решением уравнения (16) в данной ситуации является выражение
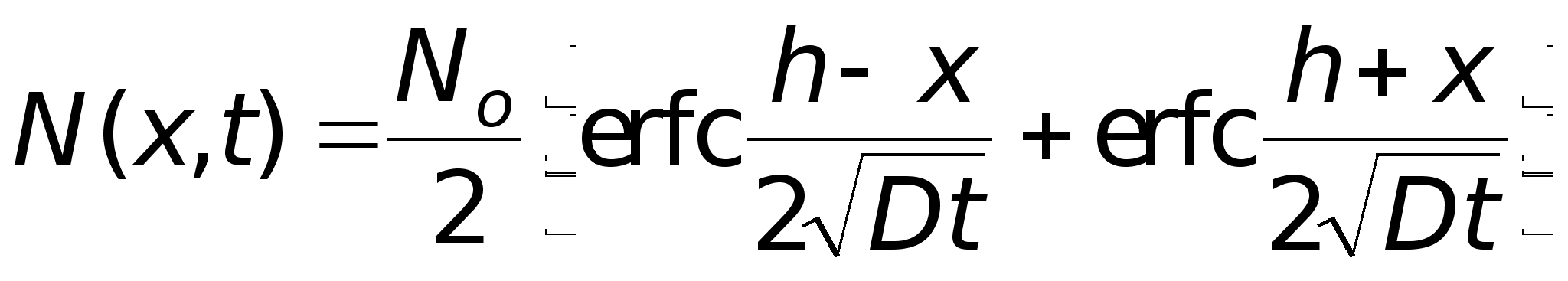 (25)
(25)
Здесь следует отметить, что erfс(-z) + erfс(z)
В отличие от диффузии из постоянного источника при диффузии из слоя конечной толщины количество диффузанта ограничено значением Q=Noh. В процессе диффузии происходит только его перераспределение и, следовательно, уменьшение со временем концентрации примеси на поверхности твердого тела.
Примером диффузии примеси из слоя конечной толщины в полубесконечное тело с отражающей границей является диффузия в кремниевую пластину из эпитаксиального, имплантированного или диффузионного слоя и покрытую слоем двуокиси кремния SiO2 или нитрида кремния Si3N4. Границу пластины и пленки можно с большой долей правдоподобия принять отражающей, т.к. коэффициенты диффузии большинства примесей в кремнии на несколько порядков больше, чем в двуокиси кремния и нитриде. Однако, равномерность распределения примеси в источнике, особенно при его создании методом диффузии или имплантации - весьма грубое и вынужденное приближение.
1.3.4 Распределение примеси при диффузии из бесконечно тонкого слоя в полубесконечное тело с отражающей границей
Решение диффузионного уравнения при этих условиях находится из предыдущего при hи условии, что количество диффузанта в источнике Q=Noh.
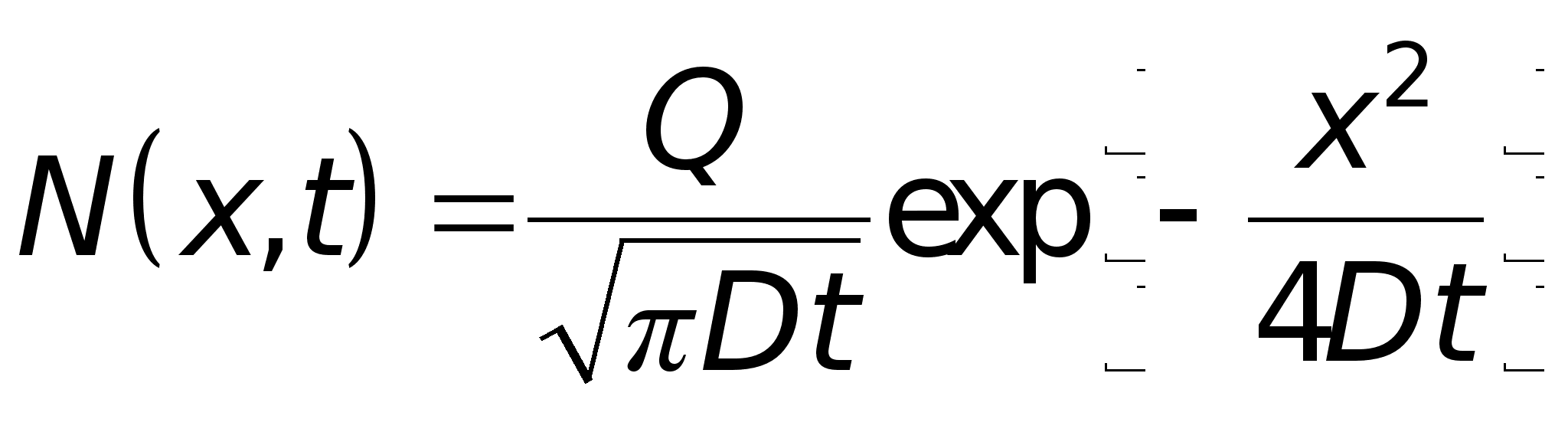 (26)
(26)
Приведенное выражение представляет собой Гауссово распределение.
Тонкий слой на поверхности полупроводниковой пластины является источником, который очень быстро истощается. Непрерывная диффузия в этом случае приводит к постоянному понижению поверхностной концентрации примеси в полупроводнике. Эту особенность данного процесса используют в полупроводниковой технологии для получения контролируемых значений низкой поверхностной концентрации примеси, например, для создания базовых областей кремниевых транзисторных структур дискретных приборов или ИМС.
На первом этапе процесса проводится кратковременная диффузия (при пониженных температурах) из постоянного источника, распределение примеси после которой описывается выражением (18). Значение Noпри этом велико и определяется либо пределом растворимости данной примеси в полупроводниковом материале, либо концентрацией примеси в стеклообразном слое на поверхности полупроводника. Этот этап часто называют загонкой. После окончания первого этапа пластины помещают в другую печь для последующей диффузии, обычно, при более высоких температурах. В этой печи нет источника примеси, а если он создается на первой стадии в виде стеклообразного слоя на поверхности пластин, его предварительно удаляют. Таким образом, тонкий слой, полученный на первом этапе, является источником перераспределяемой примеси при проведении второй стадии процесса. Для создания отражающей границы второй этап (часто называемый разгонкой) проводят в окислительной атмосфере. При этом на поверхности растет слой SiO2.
Существует заметное несоответствие между распределением примеси в источнике, сформированном при загонке, с декларируемым при выводе выражений (25) и (26) - ступенчатым. Это несоответствие должно отразиться на точности описания реального распределения примеси после второй стадии диффузии выражением (26). Не существует и объективного количественного критерия «тонкости» источника — нет каких-либо признаков, согласно которым для представления результатов данного процесса следует использовать выражение (26), а на (25) и наоборот.
При моделировании
двухстадийной
диффузии и
анализе результатов
процесса полагают,
что выражение
(26) достаточно
точно соответствует
реальному при
условии, если
величина произведения
D1t1
для первого
этапа процесса
легирования
значительно
меньше, чем
D2t2
для второго
- 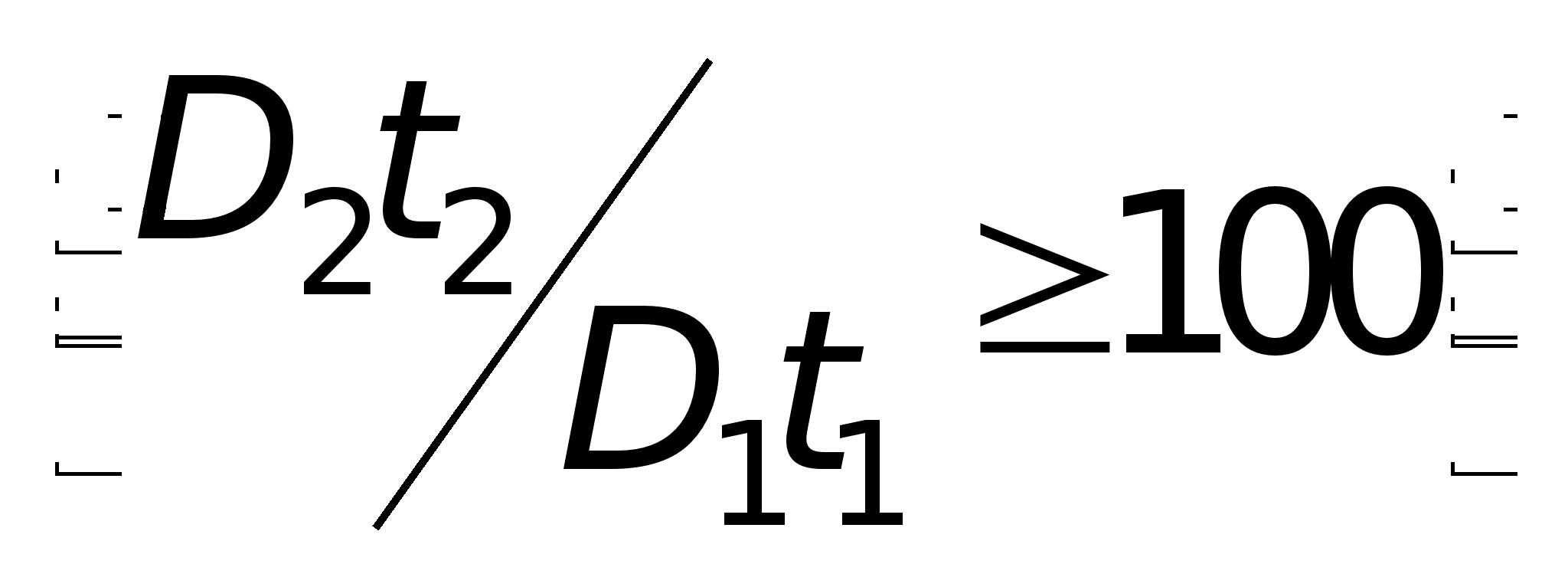 .
Это условие
быстрой
истощаемости
источника. В
этом случае,
учитывая, что
количество
накопленной
при первом
этапе примеси
определяется
соотношением
.
Это условие
быстрой
истощаемости
источника. В
этом случае,
учитывая, что
количество
накопленной
при первом
этапе примеси
определяется
соотношением
![]()
из (26) получим
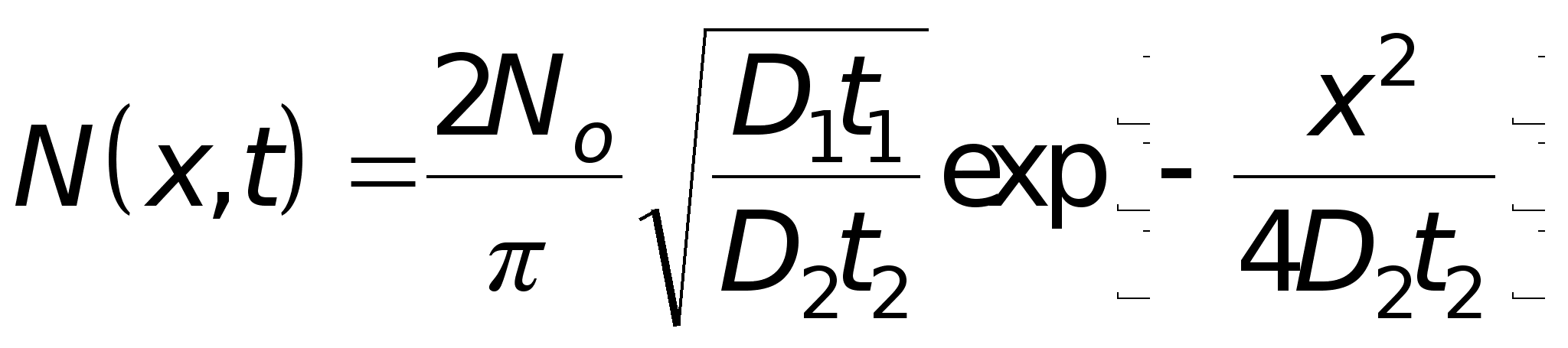 (27)
(27)
Величины D2и t2относятся ко второй стадии диффузии.
В случае, если продолжительность второй стадии не очень велика по сравнению с первой, или, иными словами, D2t2D1t1 , предположение о том, что диффузионный слой, образовавшийся в результате загонки, будет вести себя как тонкий источник неверно. В этом случае решение диффузионного уравнения будет выглядеть следующим образом
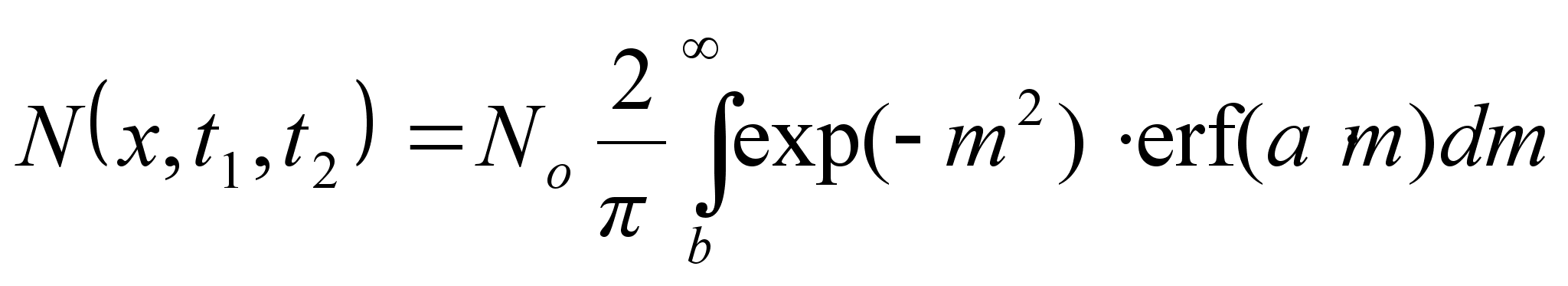 (28)
(28)
где
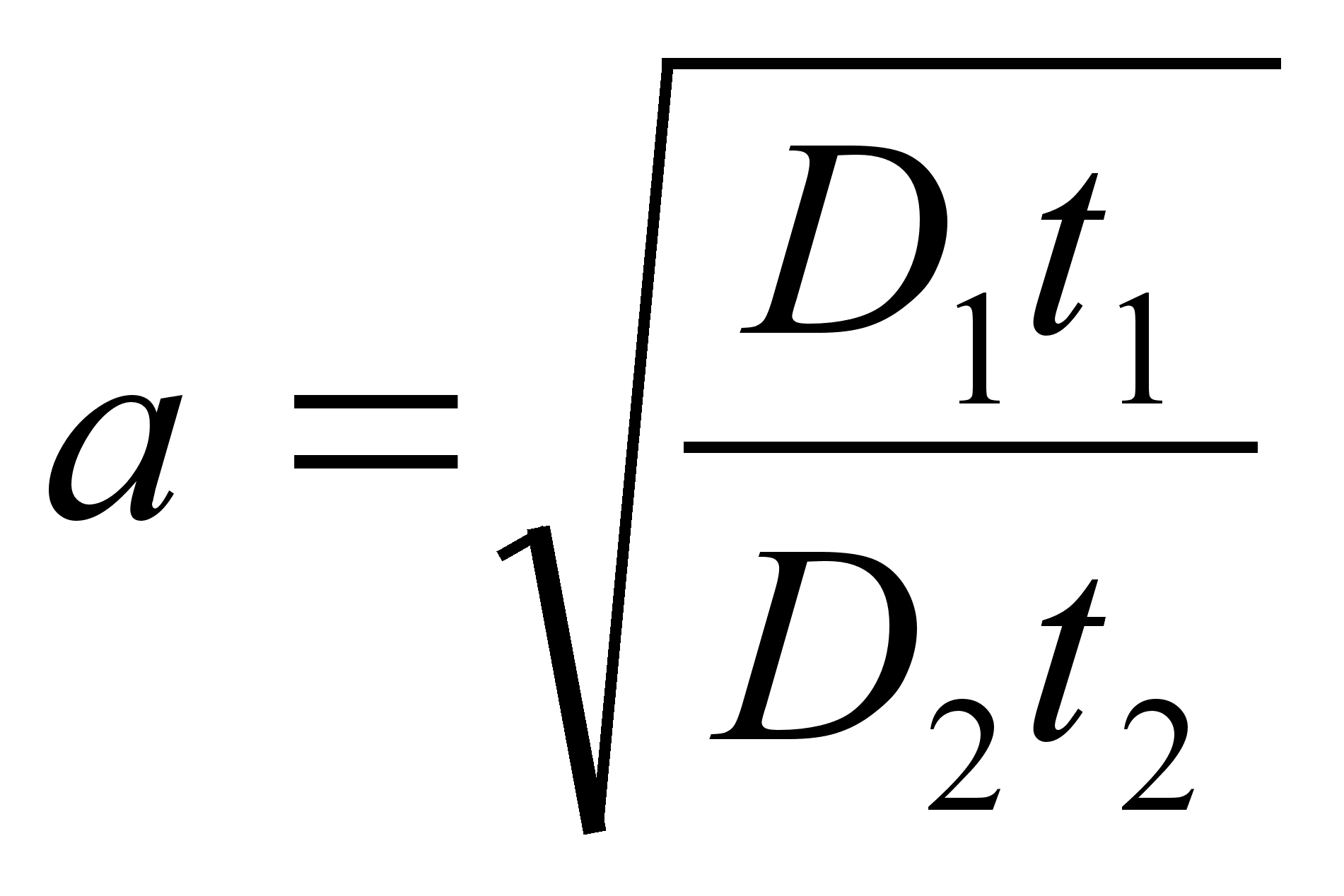 и
и 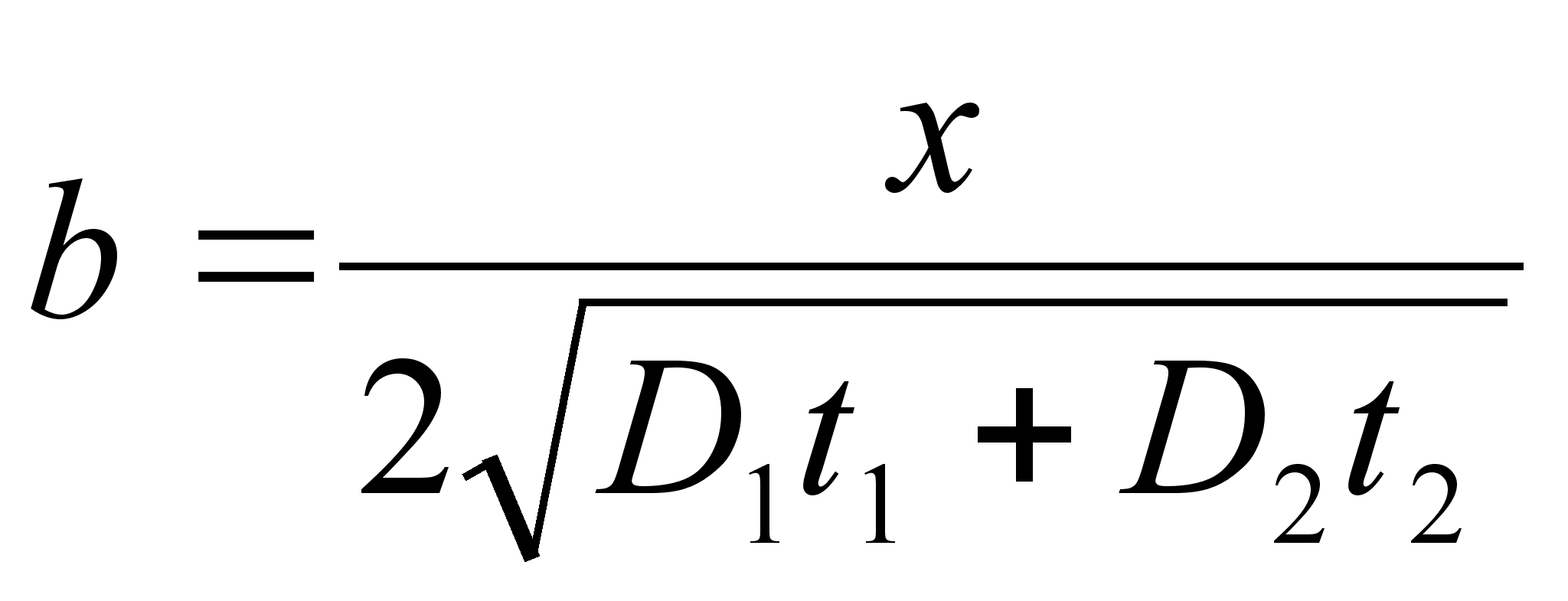
Поверхностная концентрация примеси после второй стадии диффузии выражается при данных условиях соотношением
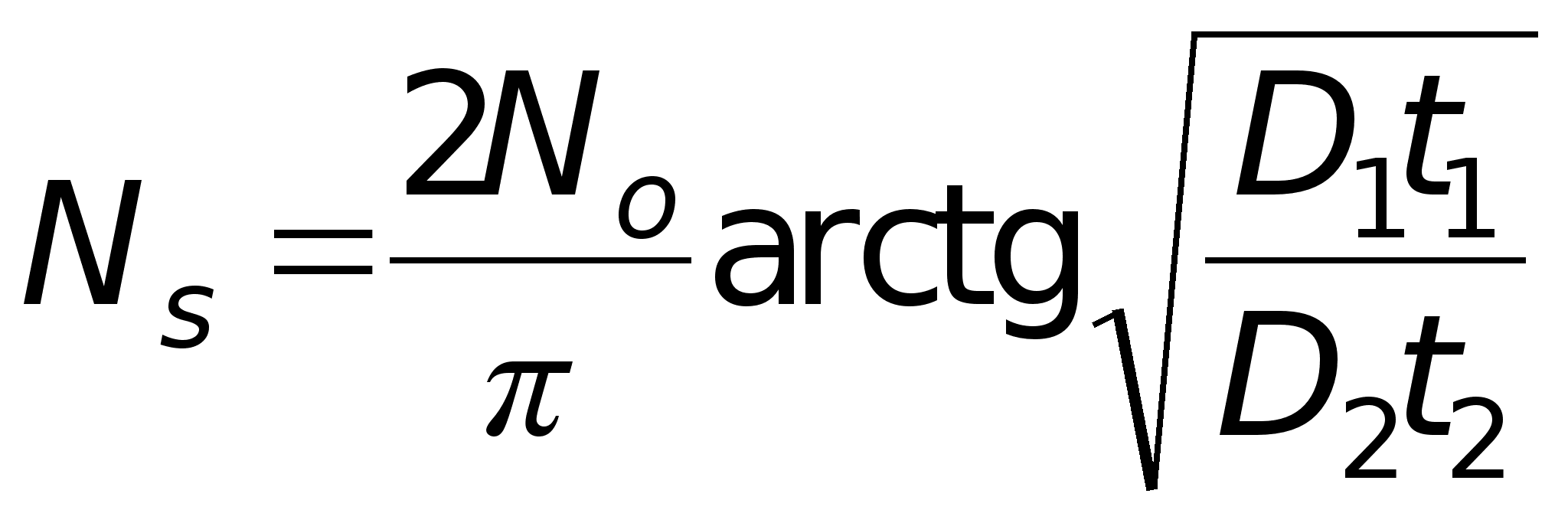 (29)
(29)
Выражение
(25) используется
для представления
распределения
при условии,
что D1t1
>D2t2 – 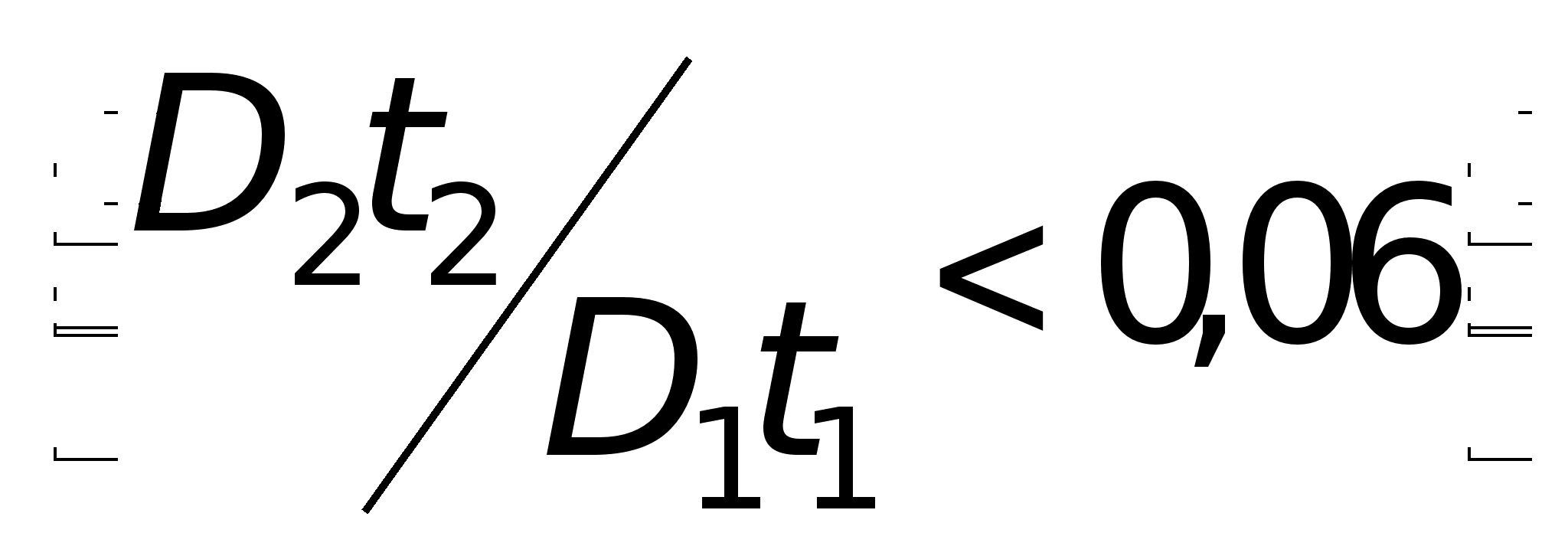 . При этом
полагают, что
. При этом
полагают, что ![]() .
.
1.4Расчет распределения примеси после диффузионного легирования.
1.4.1 Диффузия из бесконечного источника примеси на поверхности пластины и при температуре, соответствующей максимальной растворимости примеси в полупроводнике; время диффузии 30 мин.= 1800с.
Материал – кремний;
примесь – галлий.
Условия
проведения
диффузиисоответствуют
решению, представляемому
уравнением
(18).
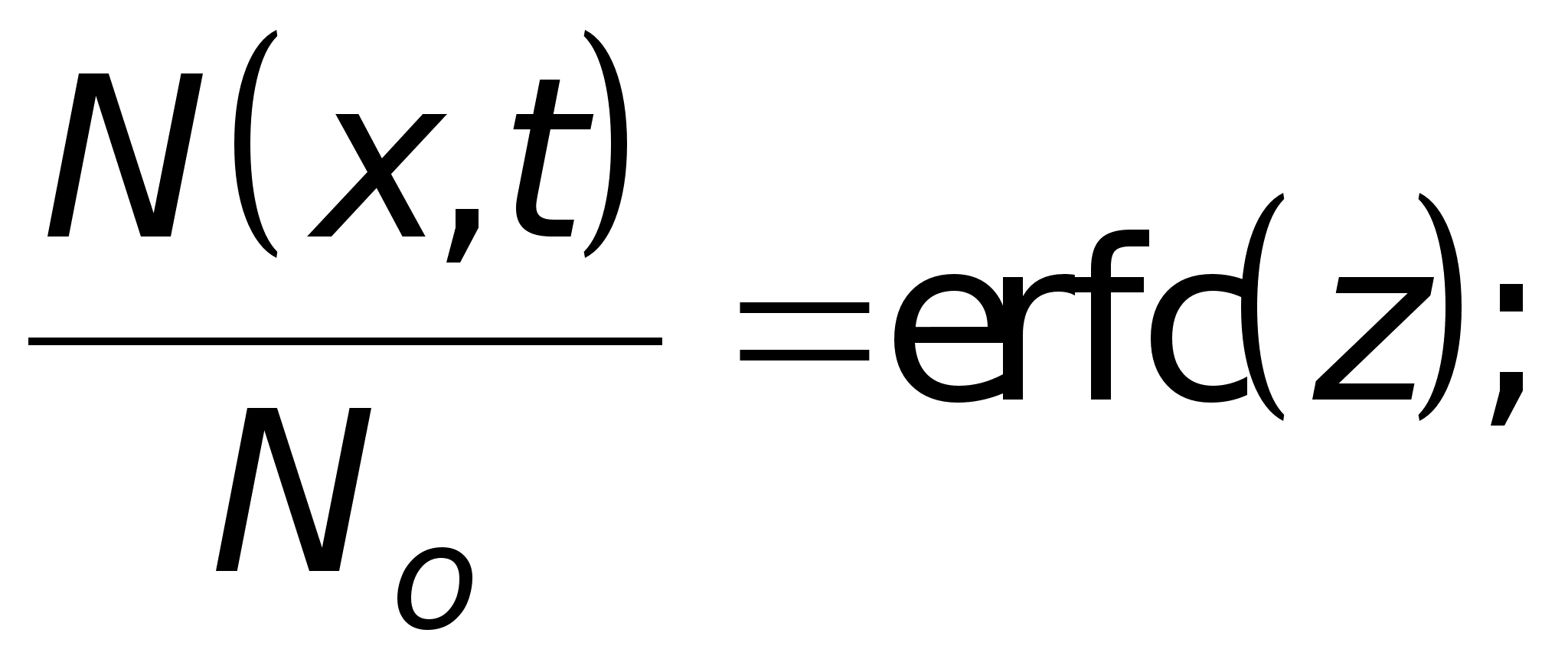
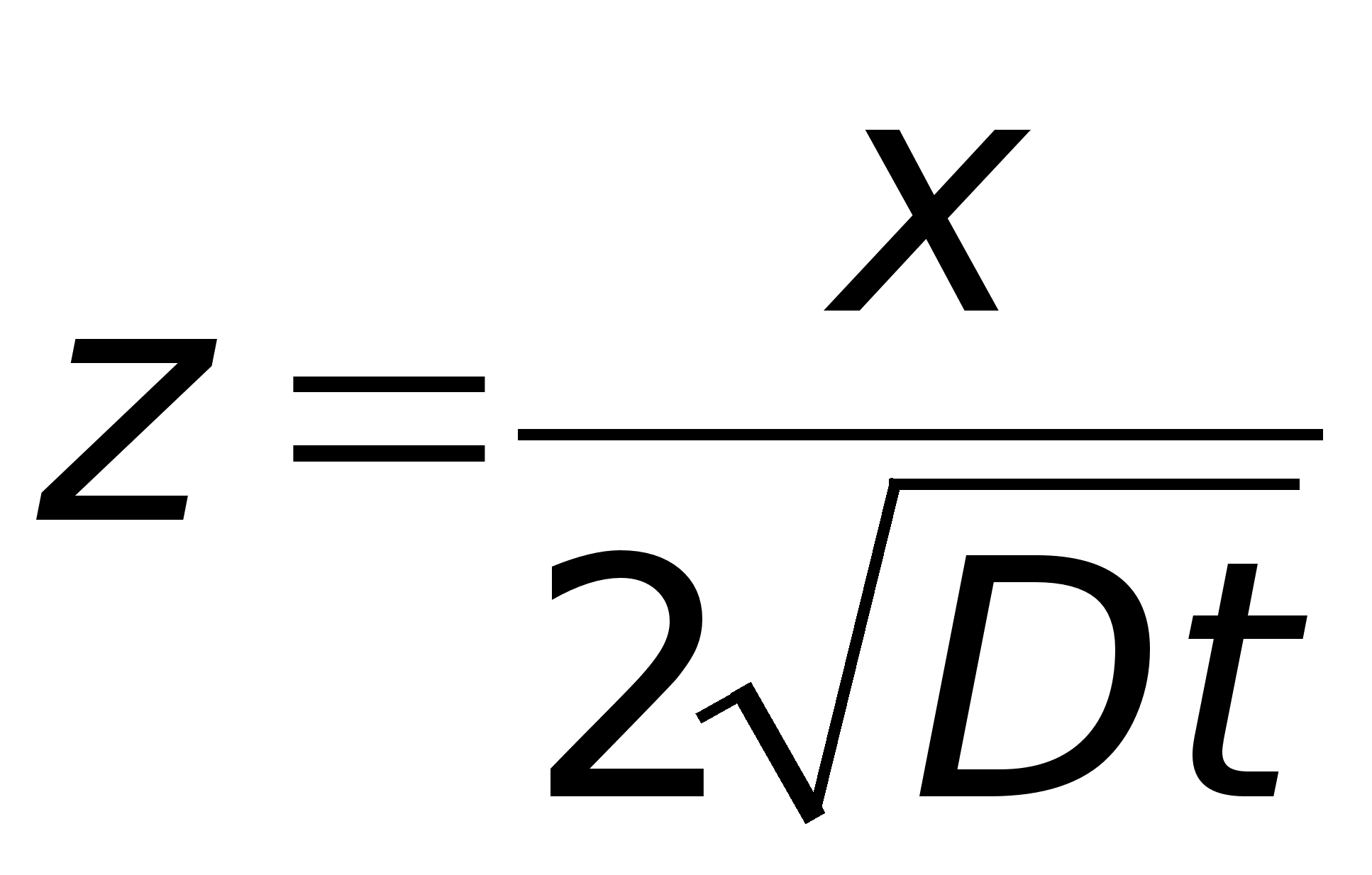 .
.
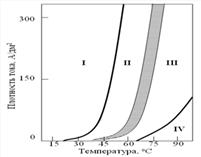
Температуру соответствующую максимальной растворимости галлия в кремнии, а так же и саму предельную растворимость найдем из графика предельной растворимости примеси в кремнии.
Nпред. раств.=N0=61019 см-3, Т=1523 К.
Коэффициент диффузии сурьмы при температуре диффузии найдемиспользуя известное выражение в форме уравнения Аррениуса
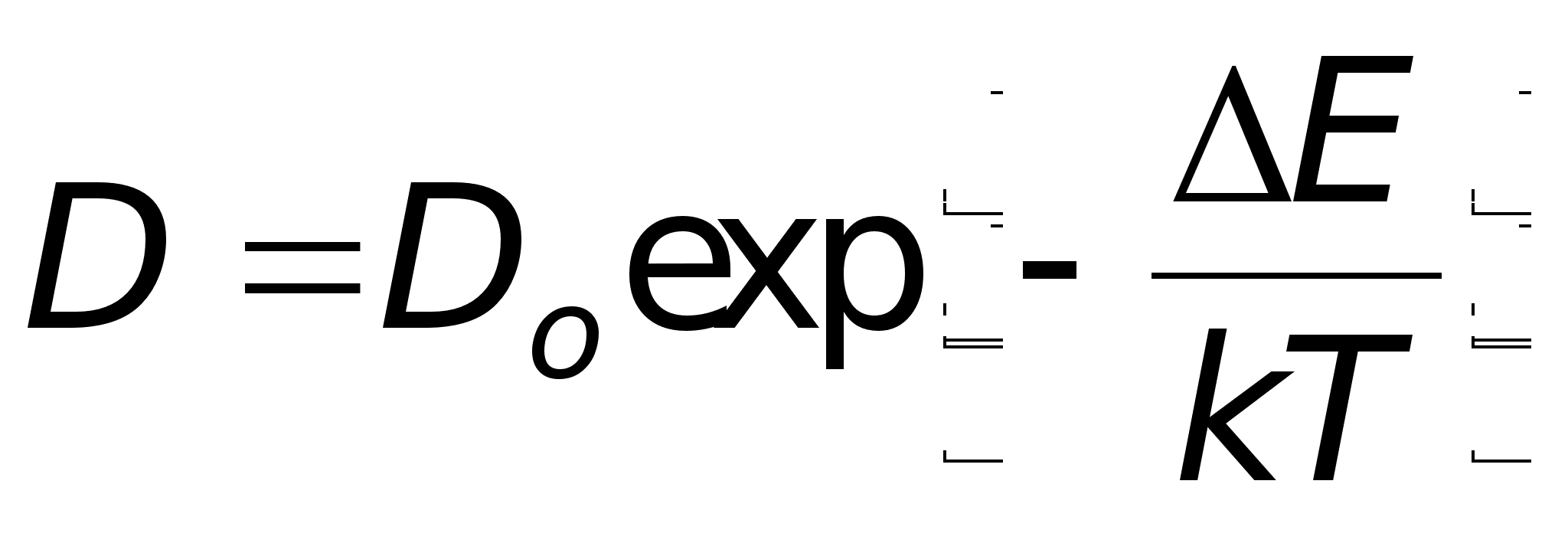 ,
,
где предэкспоненциальный множитель (постоянная диффузии) Doи энергия активации диффузии - справочные величины.
k - постоянная Больцмана, T - температура процесса в Кельвинах.
Из [5] для галлия Do=0,374 см2/с , = 3,41 эВ, при T = 1523 K D = 1,94 10-12 см2/с.
Заполняем
расчетную
таблицу,
меняя
расстояние
от x
поверхности
с необходимой
частотой, до
значения при
котором значение
N(x) имеет
порядок не
более 1012.
В первый столбец
записываем
выбранные
значения x,
во второй - ![]() .
Затем находим
значения
erfc(z), воспользовавшись
таблицей интеграла
ошибок в [4],
и вносим
эти значения
в третий
столбец.
После чего
рассчитываем
концентрации
N(x), соответствующие
каждому значению
x и результаты
записываем
в четвертый
столбец.
.
Затем находим
значения
erfc(z), воспользовавшись
таблицей интеграла
ошибок в [4],
и вносим
эти значения
в третий
столбец.
После чего
рассчитываем
концентрации
N(x), соответствующие
каждому значению
x и результаты
записываем
в четвертый
столбец.
Таблица 4 - Результаты расчета распределения галлия в кремнии
| x, мкм |
| erfc(z) | N(x), см-3 | x, мкм |
| erfc(z) | N(x), см-3 |
| 0 | 0 | 1 | 61019 | 2,5 | 2,12 | 0,002716 | 1,631017 |
| 0,5 | 0,42 | 0,552532 | 3,321019 | 3 | 2,54 | 0,000328 | 1,9681016 |
| 1 | 0,85 | 0,229332 | 1,3761019 | 3,5 | 2,96 | 0,000028 | 1,681015 |
| 1,5 | 1,27 | 0,072486 | 4,351018 | 4 | 3,38 | 0,000001753 | 1,0521014 |
| 2 | 1,69 | 0,016847 | 1,0121018 | 4,5 | 3,8 | 0,000000077 | 4,621012 |
П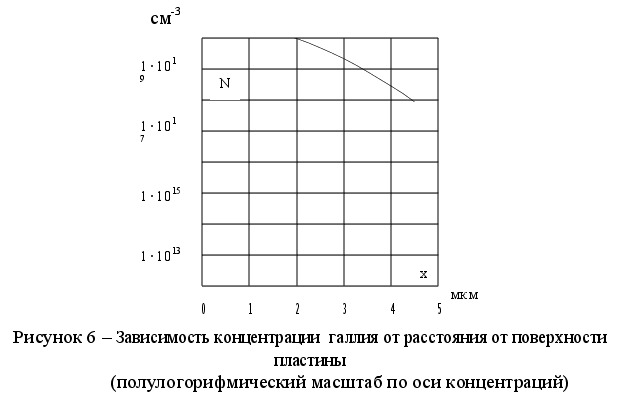 олученные
результаты
используются
для построения
графика N
= f(x) - примесного
профиля. При
построении
профиля, как
правило, используют
полулогарифмический
масштаб.
олученные
результаты
используются
для построения
графика N
= f(x) - примесного
профиля. При
построении
профиля, как
правило, используют
полулогарифмический
масштаб.
1.4.2 Диффузия из бесконечного источника примеси на поверхности пластины при Т=9500 С=1223 К, и времени диффузии 30 мин.=1800 с.
Коэффициент диффузии галлия в кремнии при Т=9500 С, N0=31019см-3.
Диффузия проходит согласно выражению (18).Дальнейший ход работы идет аналогично пункту 1.4.1. Заполняем расчетную таблицу.
Таблица 5 - Результаты расчета распределения галлия в кремнии
| x, мкм |
| erfc(z) | N(x), см-3 | x, мкм |
| erfc(z) | N(x), см-3 |
| 0 | 0 | 1 | 31019 | 0,1 | 2,05 | 0,003742 | 1,1231017 |
| 0,02 | 0,41 | 0,562031 | 1,68611019 | 0,12 | 2,46 | 0,000503 | 1,5091016 |
| 0,04 | 0,82 | 0,246189 | 7,3861018 | 0,14 | 2,87 | 0,000049 | 1,471015 |
| 0,06 | 1,23 | 0,08195 | 2,45851018 | 0,16 | 3,28 | 0,0000035 | 1,051014 |
| 0,08 | 1,64 | 0,020378 | 6,11341017 | 0,18 | 3,69 | 0,00000018 | 5,41012 |
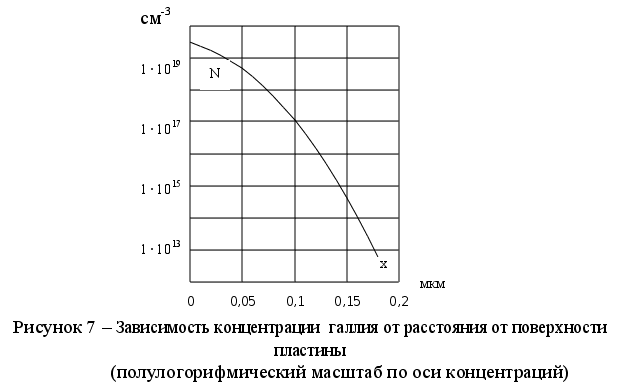
Полученные результаты используются для построения графика N = f(x) - примесного профиля. При построении профиля, как правило, используют полулогарифмический масштаб.
1.4.3 Распределение примеси после перераспределения примеси накопленной в приповерхностном слое полупроводника при Т=950ОС=1223 К и времени диффузии 30мин=1800с. Условие перераспределения полностью отражающая граница. Т=1150ОС=1423 К, время 2 часа=7200с.
Произведение D1t1 для процесса загонки равно: D1t1 = 3,3110-155,95810-12 см2
Коэффициент диффузии для процесса перераспределения примеси (Do=0,374 см2/с , = 3,41 эВ, T = 1423 K) равен D = 3,128 10-13 см2/с. Произведение D2t2 = 3,12810-132,2510-9 см2. D2t2 > D1t1(в 377 раз), т.е. условия быстрой истощаемости источника, следовательно, пользуемся для расчета распределения примеси выражением (27).
В первый столбец таблицы (6) заносим значения x, во второй значения exp(-x2/4D2t2), рассчитанные значения Ns заносим в третий столбец.
Таблица 6 - Результаты расчета распределения галлия в кремнии при диффузии из приповерхностного слоя.
| x, мкм |
| Ns , см-3 | x, мкм |
| Ns , см-3 |
| 0 | 1,0 | 9,8231017 | 1,8 | 0,02742 | 2,6931016 |
| 0,36 | 0,866 | 8,5071017 | 2,16 | 0,005633 | 5,5341015 |
| 0,72 | 0,5624 | 5,5251017 | 2,52 | 0,0008681 | 8,5271014 |
| 1,08 | 0,274 | 2,691017 | 2,88 | 0,0001 | 9,8541013 |
| 1,44 | 0,1 | 9,8311016 | 3,24 | 0,0000087 | 8,5411012 |
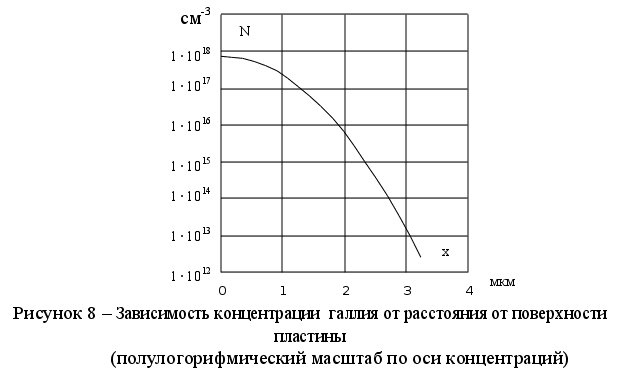 Полученные
результаты
используются
для построения
графика N
= f(x) - примесного
профиля.
Полученные
результаты
используются
для построения
графика N
= f(x) - примесного
профиля.
Заключение.
В данном курсовом проекте были рассмотрены процесс очистки полупроводникового вещества – зонная плавка и способ введения примеси в полупроводник – диффузия примеси.
Для процесса зонной плавки произведен расчет для трех очищаемых примесей: фосфор, галлий, сурьма. Результаты расчета представлены в виде таблиц и графиков: распределение удельного сопротивления и распределения каждой примеси вдоль слитка кремния после очистки зонной плавкой (один проход расплавленной зоной).
Эффективность очистки зависит от скорости кристаллизации: чем меньше скорость кристаллизации в донной примеси, тем лучше она очищается, таким образом при Vкр0 kэффk0; Vкр kэфф1. Но это не означает, что если мы уменьшим скорость кристаллизации до нуля, то получим исходное вещество в чистом виде – это лишь одно из условий очистки вещества. Определяющим является также равновесный коэффициент сегрегации (К0) , который отражает эффективность перераспределения между жидкой и твердой фазой, он должен отличаться от еденицы в большую или меньшую сторону. В нашем случае k0 Sb
Похожие работы
... с кислородом, восстановлением - отнятие кислорода. С введением в химию электронных представлений понятие окислительно-восстановительных реакций было распространено на реакции, в которых кислород не участвует. В неорганической химии окислительно-восстановительные реакции (ОВР) формально могут рассматриваться как перемещение электронов от атома одного реагента (восстановителя) к атому другого ( ...
... 3. РАСЧЕТ ОБОРУДОВАНИЯ И ПРОЕКТИРОВАНИЕ ОТДЕЛЕНИЯ 3.1 Технико-экономическое обоснование основного, дополнительного и вспомогательного оборудования Основным оборудованием термического отделения для термообработки холоднокатаного листа является агрегат непрерывного отжига. Печная часть агрегата включает многокамерную башенную печь отжига, установки и камеры ускоренного перестаривания и ...
... компонентов над расплавами соединений составляют от двух до нескольких десятков атмосфер; температура плавления большинства соединений превышает 1200° С. 1.3.Получение полупроводниковых монокристаллов соединений типа АIIBVI. Рассмотрев выше изложенные методы можно добавить , что не все соединения типа AIIBVI можно получить одним и тем ...
... которого расположены стержни, перемещающие вверх измельчаемый материал и шары. Конусная дробилка. Шаровая дробилка Для окисной высококачественной керамики используют более экономически выгодный химический метод получения керамических порошков - метод одновременного осаждения нерастворимых осадков. ...
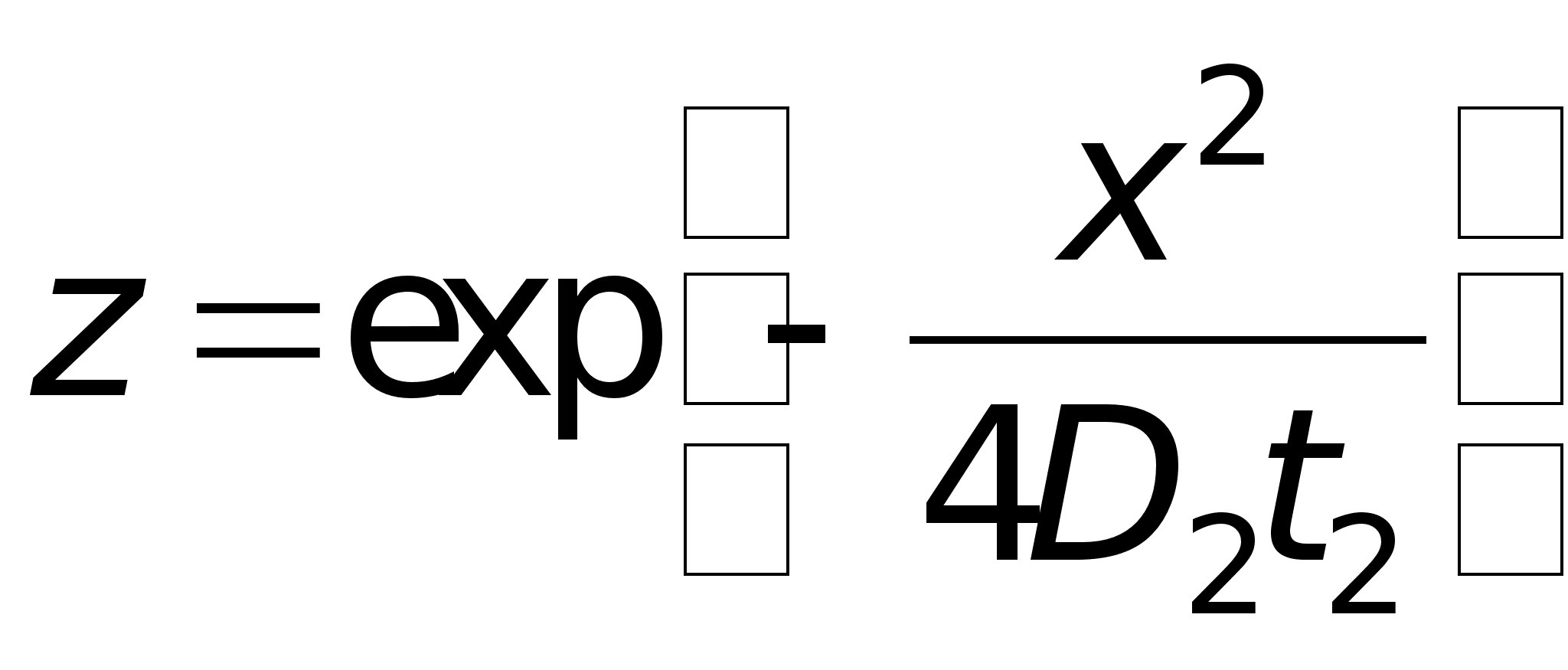

0 комментариев