Навигация
Тройные и кратные интегралы
Министерство общего и профессионального образования Р.Ф.
Иркутский государственный технический университет.
Кафедра высшей математики.
Реферат.
Применение тройных или кратных
интегралов.
Выполнила: студентка
группы ТЭ-97-1
Мелкоступова С.С.
Проверил преподаватель
кафедры высшей математики
Седых Е.И.
Иркутск 1998.
Содержание.
I. Масса неоднородного тела. Тройной интеграл.
II. Вычисление тройных интегралов.
1. Декартовы координаты.
А) Пример.
2. Цилиндрические координаты.
3. Сферические координаты.
А) Пример.
4. Применение тройных интегралов.
I. Масса неоднородного тела. Тройной интеграл.
Рассмотрим тело, занимающее пространственную область ![]() (рис. 1), и предположим, что плотность распределения массы в этом теле является непрерывной функцией координат точек тела:
(рис. 1), и предположим, что плотность распределения массы в этом теле является непрерывной функцией координат точек тела:
![]()
Единица измерения плотности - кг/м3.
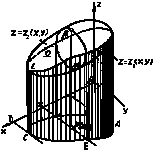
Рис. 1.
Разобьем тело произвольным образом на n частей; объемы этих частей обозначим ![]() Выберем затем в каждой части по произвольной точке
Выберем затем в каждой части по произвольной точке ![]() Полагая, что в, каждой частичной области плотность постоянна и равна ее значению в точке
Полагая, что в, каждой частичной области плотность постоянна и равна ее значению в точке ![]() , мы получим приближенное выражение для массы всего тела в виде суммы
, мы получим приближенное выражение для массы всего тела в виде суммы
![]() (*)
(*)
Предел этой суммы при условии, что ![]() и каждое частичное тело стягивается в точку (т. е. что его диаметр ) стремится к нулю), и даст массу М тела
и каждое частичное тело стягивается в точку (т. е. что его диаметр ) стремится к нулю), и даст массу М тела
![]()
Сумма (*) называется n-й интегральной суммой, а ее предел - тройным интегралом от функции ![]() по пространственной области
по пространственной области ![]() .
.
К вычислению тройного интеграла, помимо определения массы тела, приводят и другие задачи. Поэтому в дальнейшем мы будем рассматривать тройной интеграл
![]()
где ![]() - произвольная непрерывная в области
- произвольная непрерывная в области ![]() функция.
функция.
Терминология для тройных интегралов совпадает с соответствующей терминологией для двойных интегралов. Точно так же формулируется и теорема существования тройного интеграла .
Свойства двойных интегралов, полностью переносятся на тройные интегралы. Заметим только, что если подынтегральная функция ![]() тождественно равна 1, то тройной интеграл выражает объем V области
тождественно равна 1, то тройной интеграл выражает объем V области ![]() :
:
![]()
Потому свойства V и VI надо теперь сформулировать следующим образом.
V 1. Если функция ![]() во всех точках области интегрирования
во всех точках области интегрирования ![]() удовлетворяет неравенствам
удовлетворяет неравенствам
![]()
то
![]()
где V - объем области ![]() .
.
VI 1. Тройной интеграл равен произведению значения подынтегральной функции в некоторой точке области интегрирования на объем области интегрирования, т. е.
![]()
II. Вычисление тройных интегралов.
Вычисление тройного интеграла ![]() может быть осуществлено посредством ряда последовательных интегрировании. Мы ограничимся описанием соответствующих правил.
может быть осуществлено посредством ряда последовательных интегрировании. Мы ограничимся описанием соответствующих правил.
Похожие работы
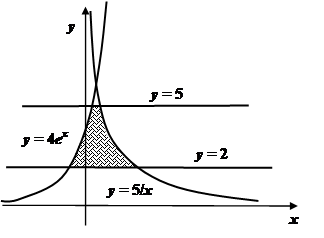
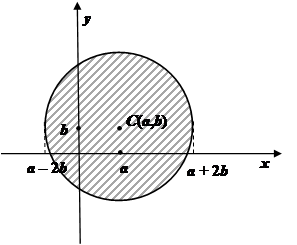
... так: , (10) где F1 и F2 – функции, полученные при подстановке в функцию f вместо x, y, z их выражений через цилиндрические (8) или сферические (9) координаты. 1.4 Геометрические и физические приложения кратных интегралов 1) Площадь плоской области S: (11) Пример 1. Найти площадь фигуры D, ограниченной линиями у = 2, у = 5. Решение. Эту площадь удобно вычислять, считая у ...
... выражения типа дивергенции по п- мерной области и интеграл по ограничивающей ее сверхповерхности S с уравнением L(x,y,z,…)=0. Если придерживаться прежних обозначений, то формула имеет вид (3) Впрочем, Остроградский не применял геометрических образов и терминов, которыми пользуемся мы: геометрия многомерных пространств в то время еще не существовала. В “Мемуаре об исчислении вариаций кратных ...
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... Из этой теоремы следует, что класс функций, представимых рядами Фурье, довольно широк. Поэтому ряды Фурье нашли широкое применение в различных отделах математики. Особенно успешно ряды Фурье применяются в математической физике и её приложениях к конкретным задачам механики и физики. Этот вопрос можно решить с помощью теоремы Дирихле. («Краткий курс высшей математики», Шнейдер и др., стр. 181) ...
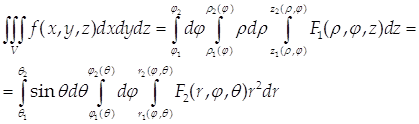
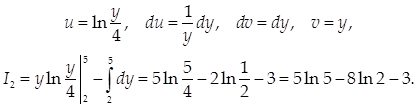
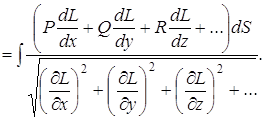
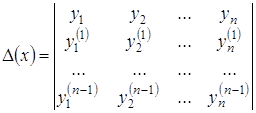





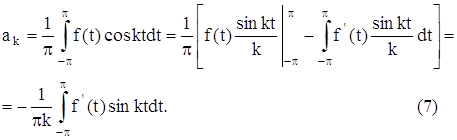
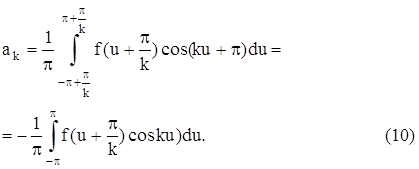
0 комментариев