Навигация
5. Доказать, что уравнение
(x + y√5)4 + (z + t√5)4 = 2 + √5
не имеет решений в рациональных числах x, y, z, t.
Можно, конечно, найти отдельно сумму членов левой части, не содержащих √5 (она должна быть равна 2), и отдельно — коэффициент при √5 (он должен равняться 1). Но что делать с полученной громоздкой системой неясно. Вместо этого воспользуемся (4) и заменим плюс перед √5 на минус!
(x – y√5)4 + (z – t√5)4 = 2 – √5.
Слева стоит неотрицательное число, справа — отрицательное.
6. Доказать, что существует бесконечно много пар (x;y) натуральных чисел, для которых x2 отличается от 2y2 на 1:
| |x2 – 2y2 | = 1. | (5) |
Несколько таких пар с небольшими (x;y) легко найти подбором: это (1;1), (3;2), (7;5), (17;12), ... (рис.1). Как продолжить этот набор? Можно ли записать общую формулу для этих решений?
|
Рис. 1. Проходят ли эти гиперболы через бесконечное число узлов клетчатой бумаги? |
Найти ответы на эти вопросы нам поможет число 1 + √2. Закономерность, позволяющая получать всё новые и новые решения (x;y), указана в таблице:
| n | (1 + √2)n | xn | yn | xn2 – 2yn2 | (1 – √2)n |
| 1 | 1 + √2 | 1 | 1 | 1 – 2 = –1 | 1 – √2 |
| 2 | 3 + 2√2 | 3 | 2 | 9 – 8 = 1 | 3 – 2√2 |
| 3 | 7 + 5√2 | 7 | 5 | 49 – 50 = –1 | 7 – 5√2 |
| 4 | 17 + 12√2 | 17 | 12 | 289 – 288 = 1 | 17 – 12√2 |
| 5 | 41 + 29√2 | 41 | 29 | 1681 – 1682 = –1 | 41 – 29√2 |
| ... | ... | ... | ... | ... | ... |
Какой будет шестая строчка?
Видно, что коэффициенты xn, yn в числе
xn + yn√2 = (1 + √2)n
будут давать нужную пару. Доказать это поможет колонка таблицы из сопряжённых чисел (мы снова применяем (4)):
xn – yn√2 = (1 – √2)n.
Перемножив два последних равенства, получим
| x | 2 n | – 2y | 2 n | = (–1)n, |
и интересующее нас выражение попеременно равно то 1, то –1. Складывая и вычитая эти же два равенства, мы получим явное выражение для xn и yn:
| xn = | (1 + √2)n + (1 – √2)n 2 | , |
| yn = | (1 + √2)n – (1 – √2)n 2√2 | . |
Можно ли в решении этой задачи про целые числа обойтись без иррациональных чисел 1 + √2 и 1 – √2? Теперь, зная ответ, мы можем легко выразить (xn+1;yn+1) через предыдущую пару (xn;yn): из xn+1 + yn+1√2 = (xn + yn√2)(1 + √2) вытекает
| xn+1 = xn + 2yn, yn+1 = xn + yn. | (6) |
До этого рекуррентного соотношения можно было, видимо, догадаться по нескольким первым решениям, а потом проверить, что
| |x | 2 n | – 2y | 2 n | | = |x | 2 n+1 | – 2y | 2 n+1 | |. |
Добавив начальное условие x1 = 1, y1 = 1, отсюда (по индукции) можно было бы заключить, что |xn2 – 2yn2| = 1 для любого n. Далее, выразив обратно (xn;yn): через (xn+1;yn+1), «методом спуска» ([8]) можно доказать, что найденной серией исчерпываются все решения уравнения (5) в натуральных числах (x;y). Подобным же образом решается любое «уравнение Пелля» x2 – dy2 = c (а к уравнениям такого типа сводится любое квадратное уравнение в целых числах x, y), но у исходного уравнения может быть несколько серий решений ([7]).
Рекуррентные соотношения типа (6) возникают не только в теории чисел, но и в разных задачах анализа, теории вероятностей. Вот характерный пример комбинаторной задачи такого типа (она предлагалась на последней международной олимпиаде в Лондоне):
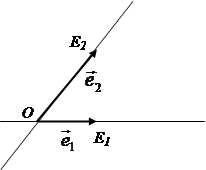
7. В вершине A правильного восьмиугольника сидит лягушка. Из любой вершины восьмиугольника, кроме вершины E, противоположной A, она может прыгнуть в любую из двух соседних вершин. Попав в E, лягушка останавливается и остаётся там. Найти количество em различных способов, которыми лягушка может попасть из вершины A в E ровно за m прыжков.
Если раскрасить вершины восьмиугольника через одну в чёрный и белый цвет (рис.2), сразу станет ясно, что e2k–1 = 0 при любом k: цвет вершин при каждом прыжке меняется. Обозначим через an и cn количество способов, которым лягушка может за 2n прыжков, попасть из вершины A, соответственно, в вершину A и в одну из вершин C (из соображений симметрии ясно, что в каждую из вершин, обозначенных на рисунке буквой C, можно попасть одним и тем же числом способов). Как легко проверить (см. рис.2а,б,в,г),
a1 = 2, c1 = 1;
| (7) |
А интересующее нас число e2n равно, очевидно, 2cn–1 (рис. 2д).
|
а) c1 = 1 |
б) a1 = 2 |
в) an+1 = 2an + 2cn |
|
г) cn+1 = an + 2cn |
д) e2n = 2cn–1 |
| Рис. 2. а) | Из A в C за два прыжка можно попасть только одним способом: c1 = 1. |
| б) | Из A в A за два прыжка можно попасть двумя способами: a1 = 2. |
| в) | В A можно попасть из C двумя способами и из A двумя способами: an+1 = 2an + 2cn. |
| г) | В C можно попасть из A одним способом и из C — двумя: cn+1 = an + 2cn. |
| д) | В E можно попасть из C двумя способами: e2n = 2cn–1. |
Как же найти явную формулу для an и cn? Запишем наше рекуррентное соотношение (7) так:
| an+1 + cn+1√2 = (an + cn√2)(2 + √2) | (8) |
и — как вы уже, конечно, догадались — ещё так:
| an+1 – cn+1√2 = (an – cn√2)(2 – √2). | (9) |
Отсюда по индукции, пользуясь (7), получаем:
| an + cn√2 = (2 + √2)n–1(a1 + c1√2) = (2 + √2)n, |
| an – cn√2 = (2 – √2)n–1(a1 – c1√2) = (2 – √2)n. |
Поэтому
| cn = | (2 + √2)n – (2 – √2)n 2√2 | , |
а так как e2n = 2cn–1, получаем окончательно
| e2n = | (2 + √2)n–1 – (2 – √2)n–1 √2 | , e2n–1 = 0. |
Задача решена. Неясно только, как в этой задаче (и в предыдущей задаче6) можно было додуматься до формул, содержащих ±√2, — ведь в задаче речь идёт о целых числах! (Для участников олимпиады и читателей «Кванта» задача7 была облегчена тем, что в формулировке указывался ответ — «Квант», 1979, №11, М595).
Однако «сопряжённые числа» возникли бы совершенно автоматически, если бы мы владели началами линейной алгебры (см.[12]), и применили стандартные правила этой науки к решению уравнений (7). Эти правила предлагают сначала выяснить, какие геометрические прогрессии (an = a0λn, cn = c0λn) удовлетворяют данному рекуррентному соотношению. Значения, для которых такие прогрессии существуют, — они называются характеристическими значениями или собственными числами — определяются из некоторого уравнения (оно тоже называется характеристическим). Для (7) характеристическое уравнение имеет вид λ2 – 4λ + 2 = 0, его корни — как раз 2 + √2 и 2 – √2. Зная эти корни, любое решение рекуррентного соотношения мы можем получить как «линейную комбинацию» соответствующих геометрических прогрессий ([11]). «Начальное условие» (в нашем случае a1 = 2, c1 = 1) определяет нужное нам решение однозначно.
Неудивительно, что даже самые простые рекуррентные целочисленные последовательности, для которых характеристическое уравнение — квадратное с целыми коэффициентами (примеры — те же (6) и (7) или последовательность Фибоначчи 1, 1, 2, 3, 5, 8, ..., Fn+1 = Fn + Fn–1; см.[9], [10]), выражаются, как функции номера, с помощью «сопряжённых» квадратичных иррациональностей.
Заметим, что большее характеристическое число определяет скорость роста последовательности: при больши́х n в задаче7 en (2 + √2)n/√2. Можно сказать это ещё так:
| en+1 en | = 2 + √2. |
Для задачи 6 аналогичное наблюдение:
| xn yn | = √2. |
Интересное продолжение этого факта мы увидим в следующей задаче с бо́льшим числом «сопряжённых» иррациональностей.
Поочерёдно меняем все знаки
Похожие работы
... 3. Соглашение о комплексных числах. 1. Действительное число а записывается также в виде a + 0i (или a – 0i). П р и м е р ы. Запись 3 + 0i обозначает то же, что запись 3. Запись –2 + 0i означает –2. 2. Комплексное число вида 0 + bi называется “чисто мнимым”. Запись bi обозначает то же, что 0 + bi. 3. Два комплекных a + bi, a’ + b’i считаются равными ...
... в сопряжённых комплексных координатах 1.1. Определение аффинного преобразования Введём определение аффинного преобразования евклидовой плоскости в сопряжённых комплексных координатах. Преобразование евклидовой плоскости называется аффинным, если оно отображает каждую прямую на прямую. [1] 1.2. Формула аффинного преобразования Мы хотим построить теорию аффинных преобразований с помощью ...
дним членам так называемой последовательности Фибоначчи: 34 и 55 или 89 и 144. Филлотаксис подсолнечника — одна из многих неожиданных встреч с последовательностью Фибоначчи. Впервые с ней столкнулся в прошлом столетии французский математик Эдуард Люка. Читая книгу «Искусство абака» знаменитого итальянского математика эпохи Возрождения Леонардо Пизанского, известного больше по прозвищу Фибоначчи, ...
... это целый класс реакций окисления органических веществ с участием катализатора, обладающего окислительно-восстановительными свойствами. Этот процесс протекает циклично т. е. состоит из многократных повторений. Колебательные химические реакции были открыты и научно обоснованы в 1951 г. советским учёным Борисом Петровичем Белоусовым. Б.П. Белоусов изучал окисление лимонной кислоты при её реакции с ...


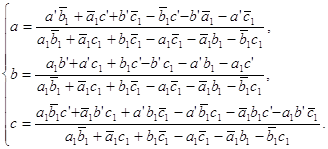
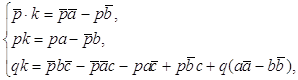
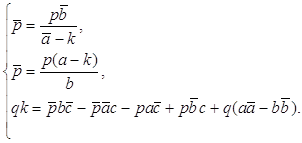
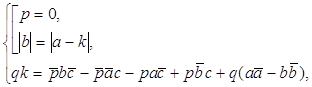
0 комментариев