Навигация
8. Пусть
(1 + √2 + √3)n = qn + rn√2 + sn√3 + tn√6,
где qn, rn, sn и tn — целые числа. Найти пределы
| rn qn | , |
| sn qn | , |
| tn qn | . |
Конечно, мы здесь можем выразить (qn+1; rn+1; sn+1; tn+1) через (qn; rn; sn; tn), пользуясь тем, что
qn+1 + rn+1√2 + sn+1√3 + tn+1√6 = (1 + √2 + √3)(qn + rn√2 + sn√3 + tn√6),
но, наученные опытом, мы уже знаем, что более простые формулы получаются не для самих чисел qn, rn, sn, tn, a для некоторых их комбинаций. Одну такую комбинацию мы уже знаем: это
qn + rn√2 + sn√3 + tn√6 = (1 + √2 + √3)n.
Нетрудно сообразить, каковы будут другие. Рассмотрим вместе с данным числом
λ1 = 1 + √2 + √3,
ещё три «сопряжённых»:
λ2 = 1 – √2 + √3, λ3 = 1 + √2 – √3, λ4 = 1 – √2 – √3.
Тогда
qn – rn√2 + sn√3 – tn√6 = λ2n,
qn + rn√2 – sn√3 – tn√6 = λ3n,
qn – rn√2 – sn√3 + tn√6 = λ4n.
Мы можем выразить qn, rn, sn, tn через λ1, λ2, λ3, λ4:
| qn = | λ1n + λ2n + λ3n + λ4n 4 | , | sn = | λ1n + λ2n – λ3n – λ4n 4√3 | , | |
| rn = | λ1n – λ2n + λ3n – λ4n 4√2 | , | tn = | λ1n – λ2n – λ3n + λ4n 4√6 | . |
Теперь заметим, что λ1 > |λ2|, λ1 > |λ3|, λ1 > |λ4|. Поэтому
| rn qn | = |
| 1 – (λ2/λ1)n + (λ3/λ1)n – (λ4/λ1)n 1 + (λ2/λ1)n + (λ3/λ1)n + (λ4/λ1)n | · | 1 √2 | = | 1 √2 | . |
Аналогично найдём, что
| sn qn | = | 1 √3 | и |
| tn qn | = | 1 √6 | . |
Мы говорили выше, что сопряжённые числа a ± b√d возникают часто как корни квадратного уравнения с целыми коэффициентами. В связи с последней задачей возникает такое желание:
Похожие работы
... 3. Соглашение о комплексных числах. 1. Действительное число а записывается также в виде a + 0i (или a – 0i). П р и м е р ы. Запись 3 + 0i обозначает то же, что запись 3. Запись –2 + 0i означает –2. 2. Комплексное число вида 0 + bi называется “чисто мнимым”. Запись bi обозначает то же, что 0 + bi. 3. Два комплекных a + bi, a’ + b’i считаются равными ...
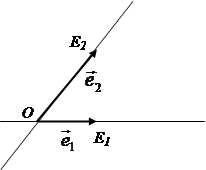
... в сопряжённых комплексных координатах 1.1. Определение аффинного преобразования Введём определение аффинного преобразования евклидовой плоскости в сопряжённых комплексных координатах. Преобразование евклидовой плоскости называется аффинным, если оно отображает каждую прямую на прямую. [1] 1.2. Формула аффинного преобразования Мы хотим построить теорию аффинных преобразований с помощью ...
дним членам так называемой последовательности Фибоначчи: 34 и 55 или 89 и 144. Филлотаксис подсолнечника — одна из многих неожиданных встреч с последовательностью Фибоначчи. Впервые с ней столкнулся в прошлом столетии французский математик Эдуард Люка. Читая книгу «Искусство абака» знаменитого итальянского математика эпохи Возрождения Леонардо Пизанского, известного больше по прозвищу Фибоначчи, ...
... это целый класс реакций окисления органических веществ с участием катализатора, обладающего окислительно-восстановительными свойствами. Этот процесс протекает циклично т. е. состоит из многократных повторений. Колебательные химические реакции были открыты и научно обоснованы в 1951 г. советским учёным Борисом Петровичем Белоусовым. Б.П. Белоусов изучал окисление лимонной кислоты при её реакции с ...
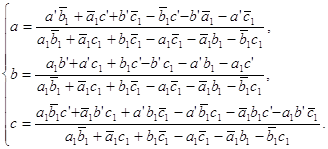
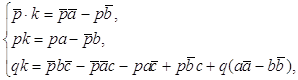
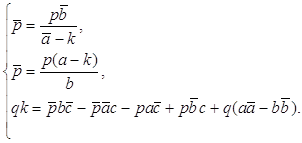
0 комментариев