Навигация
1.2.1. Определение понятий
Развитию мышления способствует работа над научными понятиями. Понятие – это продукт мышления, оно отражает реальный мир, предстает в познании как средство общения, т.е. специфически человеческой активности, выражается посредством речи, записи или символом. Понятие – это вывод, итог познания реальных процессов и явлений. Мысль, в которой отражаются общие, отличительные (специфические) признаки предметов и явлений действительности (21).
Понятие – форма научного познания, отражающая существенное в изучаемых объектах и закрепляемая специальными терминами. В математике понятие обозначается часто не только термином (слово или группа слов) – названием, но и символом – знаком. Понятие – это мысленное воспроизведение объекта (12).
Термин “понятие” обычно применяется для обозначения мысленного образа некоторого класса вещей, процессов, отношений объективной реальности или нашего сознания.
Математические понятия отражают в нашем мышлении определенные формы и отношения действительности, абстрагированные от реальных ситуаций (14).
Итак, понятие – это форма мышления, в которой отражены существенные (отличительные) свойства объектов изучения (13).
Источниками образования понятий являются: жизненный опыт учащихся, их повседневные наблюдения, восприятие различной информации, здравый смысл и бытующие устаревшие традиции (всё это можно отнести к стихийному образованию понятий); специальное формирование научных понятий учителями на уроках, усвоение понятий учащимися в процессе самостоятельной работы (в этом случае не исключается использование ассоциаций, имеющих случайный характер и приводящих к ошибкам).
Для образования понятия необходимо знать мыслительные операции и уметь ими пользоваться. Без анализа действительности – предметов и явлений – невозможно глубоко изучить их, без синтеза – соединить разъединенные части в единое целое, без обобщения – сделать вывод, а затем сформулировать понятие. В процессе изучения реальной действительности формирование понятий – цель мысленной деятельности человека, а знание операций мышления – средство, с помощью которого достигается эта цель. Но в сложном процессе образования понятия сами мыслительные операции учащегося непрерывно совершенствуются, модернизируются, поднимаются на более высокий уровень. Это можно использовать в учебной деятельности. Теперь развитие операций мышления учащегося становится целью, а образование понятий – средством, способствующим её достижению.
Понятие характеризуется содержанием, объемом, связями (и отношениями) с другими понятиями.
Содержание понятия – это множество всех существенных признаков данного понятия.
Объем понятия – это множество объектов, к которым применимо данное понятие. По объему различают единичные понятия (объем их равен единице), общие понятия (их объем больше единицы) и понятия – категории – понятия самой широкой общности.
Между содержанием и объемом понятия существует обратная зависимость: чем шире содержание понятия, тем уже его объем, и, наоборот, чем уже содержание, тем шире его объем.
Связи и отношения между понятиями отражают действительно существующие разнообразные связи между явлениями природы, общества и мышления человека. Одни из них являются ближними, существенными, другие – отдаленными, опосредствованными.
В логике понятия делят на единичные и общие, на конкретные и абстрактные, на относительные и безотносительные.
Обобщением понятия называется переход от менее общих понятий к более общим. Оно происходит путем отбрасывания основных признаков понятия, т.е. признаков, принадлежащих всем объектам, входящим в объем обобщаемого понятия. Ограничением (конкретизацией) понятия называется, наоборот, переход от более общих понятий к менее общим, объем понятия при этом сужается, а содержание расширяется.
Понятие образуется при помощи операций анализа и синтеза, абстракции и обобщения. Содержание понятия раскрывается путем описания или с помощью определения, а объем – с помощью классификации (21).
Процесс раскрытия содержания понятия состоит в перечислении его признаков. Перечисление необходимых и достаточных признаков понятия, сведенных в связное предложение (речевое или символическое), есть определение понятия (математического объекта). Каждый из признаков, входящих в определение, должен быть необходим, а все вместе – достаточны для установления данного понятия. В определении должно раскрываться основное содержание понятия. В нем не должно содержаться лишних слов; не должно быть и пропусков (13).
К отысканию ближайшего рода следует стремиться потому, что в таком случае мы подходим ближе к определяемому понятию, его объему и благодаря этому уменьшается совокупность видовых признаков в определении. Такое определение состоит из определяемого понятия, логической связки и родового понятия с видовыми признаками. Определение будет логически правильным, если между двумя его основными составными частями существует отношение равенства. Иначе говоря, по отношению друг к другу не должны быть не слишком широкими, ни слишком узкими (если упущен один из существенных признаков или включен признак, присущий не всем определяемым объектам) (12).
Определяя понятия, руководствуются правилами:
определение должно быть соразмерным, т.е. объем определяемого понятия должен быть равен объему определяющего понятия; родовое понятие должно быть ближайшим родом по отношению к определяемому понятию; видовые отличия должны быть присущи только определяемому понятию; определение должно быть кратким и ясным (21).Существуют логические формы, которые не являются определениями, но близки к определению, иногда заменяют или дополняют его.
Описание понятия обычно применяется в тех случаях, если невозможно или нецелесообразно вводить определение. Таким способом вводятся первичные (основные) математические понятия. В определении определяемое понятие сводится к уже известному понятию, но самое первое понятие каждой науки не к чему сводить, поэтому ввести его через определение невозможно.
Описание понятия может не только заменять определение, но и дополнять его такой информацией, которая конкретизирует понятие, расширяет связи с другими понятиями, полнее раскрывает его содержание, помогает учащимся глубже понять и прочнее усвоить новое понятие (12).
Похожие работы
... поколения, поставленными обществом. Методика обучения математике призвана исследовать проблемы математического образования, обучения математике и математического воспитания. Методика преподавания математики в средней школе возникла с целью поиска педагогически целесообразных путей и способов изложения учебного материала. Методика преподавания математики начала разрабатываться чешским учёным ...
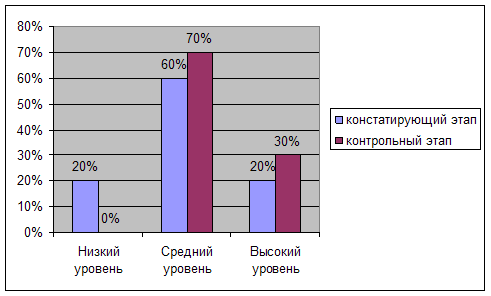
... уровня сформированности представлений о функциональной зависимости у младших школьников. 2 этап – формирующий этап - разработан и реализован комплекс упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников. 3 этап – контрольный этап - проведен анализ эффективности занятий с применением комплекса упражнений, направленных на формирование ...
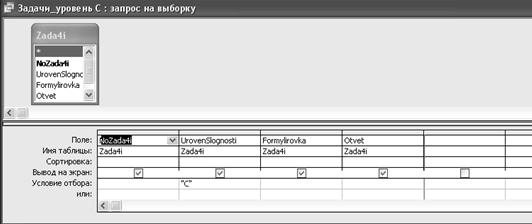
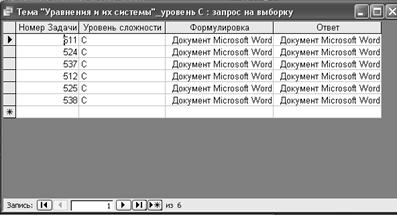
... в процессе обучения, необходима разработка совершенно новых подходов к работе с таким видом информационных ресурсов как базы данных. Глава 2.Технология использования баз данных математических задач в процессе подготовки учащихся к ЕГЭ по математике 2.1 Реализация модели В соответствии с теорией поэтапного формирования умственных действий учащихся, подготовку к сдаче единого ...
... вероятностей совместимых событий; формулы: полной вероятности, Бейеса (Байеса). Одной из форм дифференцированного обучения по курсу теории вероятностей может являться факультативный курс. 2. Разработка программы факультативного курса по теории вероятностей в курсе математики 8 класса 2.1 Основные понятия о факультативном курсе Возможность 1-2 часа в неделю дополнительно работать со ...

0 комментариев