Навигация
2.2. Формирующая часть
Итак, было проведено 10 занятий. На первых двух занятиях, после объявления цели введения комплексных чисел, ребятам рассказывалась историческая справка о развитии теории комплексного числа. Учащиеся слушали очень внимательно, проявили глубокую заинтересованность. После того, как было дано определение, основные соглашения, относящиеся к комплексным числам, ученикам было предложено самим отыскать правила действий (сложения, вычитания) над комплексными числами. Школьники очень активно включились в работу, после недолгих рассуждений, пришли к верному решению данного им задания. И это говорит о гибкости их мышления. После демонстрации нескольких примеров, иллюстрирующих операции умножения и деления комплексных чисел в алгебраической форме, учащимся были предложены подобные задания.
Несколько учащихся, по желанию, решали эти задачи у доски, а с мест, по просьбе учителя, их решения комментировали другие учащиеся. Т.о. в учебно-познавательный процесс было вовлечено как можно больше учащихся. Работа наиболее активных ребят оценивалась, с более же пассивными учениками велась индивидуальная работа. Учитель подходил к учащимся, у которых возникали вопросы по ходу решения и помогал отыскать ошибки, разобраться в решении, т.д.
После рассмотрения геометрической интерпретации комплексного числа, уже после разбора нескольких заданий, ребята в быстром темпе и с необходимыми объяснениями решали предложенные задания.
Упражнениям на закрепление было отведено третье занятие. В начале проводился фронтальный опрос. Учащиеся активно отвечали на вопросы, помогали тем, кто затруднялся, некоторые делали хорошие добавления, в основном, конечно, это сильные учащиеся. Учащиеся со средней и слабой успеваемостью, в основном, усвоили алгоритмы решения задач, а теоретические положения темы если и запомнили, то поверхностно, формально. Неточно формулировали определения комплексного числа, например, комплексные числа – это числа вида а+bi, где i2=-1. Но здесь важно такое уточнение, что a и bÎ R.
Был предложен ряд упражнений, которые ребята решали на местах, но тем учащимся, у которых возникали вопросы по ходу решения, например, что бы решить задачу z2-(5+2i)z+5+5i=0 нужно ли расписывать z в виде x+yi, предлагалось выйти к доске и найти самим ответ на свой вопрос с помощью класса или самостоятельно. Если ученик разберется в этом сам, то в следующий раз он уже будет видеть сразу способ решения.
На следующих двух занятиях мы рассматривали переход от алгебраической формы комплексного числа к тригонометрической и обратно. На предыдущем занятии им было задано повторить формулы тригонометрии, т.к. они нам понадобятся на этом занятии. После объяснения новой темы и демонстрации примера, одним из учащихся был задан хороший вопрос: “Почему переводя число 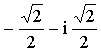 в тригонометрическую форму мы берем аргумент
в тригонометрическую форму мы берем аргумент ![]() , а не
, а не ![]() ?”. После недолгих рассуждений всем классом мы выяснили, что
?”. После недолгих рассуждений всем классом мы выяснили, что ![]() не является тригонометрической формой комплексного числа. Далее выполняя задачи на закрепление ребята проговаривали каждый шаг решения и объясняли его. Учащиеся, которые решали вперед, помогали тем, у кого возникали затруднения.
не является тригонометрической формой комплексного числа. Далее выполняя задачи на закрепление ребята проговаривали каждый шаг решения и объясняли его. Учащиеся, которые решали вперед, помогали тем, у кого возникали затруднения.
На шестом и седьмом занятиях мы разбирали действия над комплексными числами в тригонометрической форме – умножение, деление, возведение в степень, извлечение корня n-ой степени. После рассмотрения операции умножения ребята сделали верное предположение относительно деления комплексных чисел в тригонометрической форме. А далее, по аналогии с умножением, сами нашли правила возведения комплексного числа в натуральную степень. После того как разобрали примеры, перешли к извлечению корня. Как и предполагалось, у учащихся эта тема вызвала некоторые затруднения. Ребята иногда путали в формуле
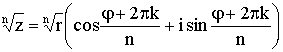 какая буква k или n пробегает значение от 0 до (n-1). Но после решения ряда закрепляющих задач у большинства учащихся сложилось четкое представление этого понятия. Также мы постарались разобрать как можно больше упражнений, чтобы у ребят не осталось неясных мест, пробелов. В работу старались включить как можно больше учащихся: проводили комментированное письмо, где каждый шаг решения объясняли разные учащиеся. Сразу несколько задач было решено на доске, но рассказать, пояснить решения пытались другие ученики. Старались включить в работу как можно больше слабых учащихся.
какая буква k или n пробегает значение от 0 до (n-1). Но после решения ряда закрепляющих задач у большинства учащихся сложилось четкое представление этого понятия. Также мы постарались разобрать как можно больше упражнений, чтобы у ребят не осталось неясных мест, пробелов. В работу старались включить как можно больше учащихся: проводили комментированное письмо, где каждый шаг решения объясняли разные учащиеся. Сразу несколько задач было решено на доске, но рассказать, пояснить решения пытались другие ученики. Старались включить в работу как можно больше слабых учащихся.
Восьмое и девятое занятия были посвящены решению упражнений, нахождению корней уравнений. На каждом занятии выделялось время, чтобы повторить некоторые моменты из предыдущих тем, чтобы не нарушать целостности темы, чтобы была системность и общность понимания. Т.к., в основном, алгоритмы решения данных задач им известны из предыдущего материала, то акцент делался на идею решения задачи. Многие ребята шли вперед и решали резервные задания. Далее класс разбился по парам, в составе которых, были, по возможности, сильный и слабый учащиеся, и продолжали решать на местах в парах. Учитель в это время следил за работой, помогал тем, у кого возникали сомнения. Хочется отметить, что чаще были вопросы по оформлению, чем по содержанию материала.
На некоторых занятиях проводились небольшие самостоятельные работы, тематические диктанты, чтобы выяснить насколько полно учащиеся освоили данное понятие, умеют ли они ими пользоваться при решении задач, знают ли связи между понятиями. Мы отмечали, что такая работа важна в первую очередь для них, т.к. они могут самостоятельно оценить уровень своих ЗУН по данным темам. Также два раза задавались на дом творческие задания, т.е. нужно было придумать самостоятельно задачу и решить ее. Сильные учащиеся очень ответственно отнеслись к этим заданиям. Но вот слабые иногда пользовались трудом своих одноклассников.
Но в целом ребята проявили большую заинтересованность, говорили, что особых трудностей тема не вызвала, это подтвердила контрольная работа. проведенная на последнем – десятом – занятии.
ЗаключениеТаким образом, после работы с научной и методической литературой по изучаемой теме делаем следующие выводы:
мышление старшеклассников становится более глубоким, полным, разносторонним и все более абстрактным; учебная деятельность старших школьников предъявляет гораздо более высокие требования к их активности и самостоятельности; развитию мышления способствует работа над научными понятиями. Процесс формирования понятия – это длительный и сложный процесс, которому следует уделять достаточное внимание.Разрабатывая логическую структуру темы “Комплексные числа” и после проведения эксперимента в школе можем сделать следующие выводы:
Изучение этой темы преследует следующие основные цели: повышение математической культуры учащихся; углубление представлений о понятии числа; дальнейшее развитие представлений о единстве математики как науки.Учащиеся способны в 10 классе усвоить понятие комплексного числа, как показало экспериментальное исследование. Учащиеся вполне успешно усваивают содержание и объем понятия комплексного числа, связи и отношения данного понятия с другими, а также умеют оперировать этим понятием при решении практических задач. Методические рекомендацииПредлагаем следующую расчасовку по темам, учитывая включение в учебный план общеобразовательного курса темы “Комплексные числа”:
Х класс (85ч).
Тригонометрические функции (15ч). Тригонометрические уравнения (13ч). Комплексные числа (14ч). Производная (16ч). Применение производной (20ч). Повторение. Решение задач (7ч).XI класс (68ч).
Повторение. Решение задач (6ч). Первообразная и интеграл (16ч). Показательная, логарифмическая и степенная функции (26ч). Повторение. Решение задач (20ч).Тему “Комплексные числа” благоприятнее всего вводить в 10 классе в I полугодии, когда сформировано представление о действительном числе и пройден курс тригонометрии.
Литература Алгебра и начала анализа./Под ред. Яковлева Г.Н. Ч2 - М.: 1987. Андронов И.К. Математика действительных и комплексных чисел. – М.: Просвещение, 1975. Брадис В.М. Методика преподавания математики в средней школе. – М.: 1951. Виленкин Н.Я. Алгебра и математический анализ 11. – М.: Просвещение, 1995. Вопросы общей методики преподавания математики. – М.: Просвещение, 1979. Демидов В.П. Методика преподавания математики. – Саранск, 1976. Крамор В.С. Алгебра и начала анализа. – М.: Высшая школа, 1981. Крутецкий В.А. Психология. – М.: Просвещение, 1980. Крутецкий В.А. Психология обучения и воспитания школьников. – М.: Просвещение, 1976. Кузмин Р.О., Фадеев Д.К. Алгебра и арифметика комплексных чисел. – Л.: Изд. Наркомпроса РСФСР, 1939. Лылова О.В. Комплексные числа и их обобщение.//Дипломная работа. – Оренбург, 1994. Метельский Н.В. Дидактика математики. – Минкс: Изд-во БГУ им. В.И. Ленина, 1982. Методика преподавания математики в средней школе. Общая методика./Оганесян В.А. и др. – М.: Просвещение, 1980. Методика преподавания математики в средней школе. Общая методика. – М.: Просвещение, 1985. Методика факультативных занятий в 9-10 классах. Избранные вопросы математики. – М.: Просвещение, 1983. Немов Р.С. Психология. Общие основы психологии. Т1. – М.: 1995. Немов Р.С. Психология. Психология образования. Т2. – М.: 1995. Педагогика./Под ред. Пидкасистого П.И. – М.: Пед. общество России, 1998. Петровский А.В. и др. Психология. – М.: Академия, 1998. Подласый И.П. Педагогика. – М.: Просвещение, 1996. Поспелов Н.Н. и др. Формирование мыслительных операций у старшеклассников. – М.: Педагогика, 1989. Программно-методические материалы. Математика 5-11 классы. Сборник нормативных документов. – М.: Дрофа, 1998. Программно-методические материалы. Математика 5-11 классы. Тематическое планирование. – М.: Дрофа, 1998. Психология. Словарь. – М.: Изд. политической литературы, 1990. Сергиенко Л.Ю. и др. Планирование учебного процесса по математике. – М.: Высшая школа, 1987. Сластенин В.А. и др. Педагогика. – М.: 1998. Хинчин А.Я. Педагогические статьи. – М.: Академия пед. наук РСФСР, 1963. Холодченко А.А. Проблемные задачи как основа для дифференциации обучения в старших классах.//Дипломная работа. – Оренбург, 1997. Приложение 2 Теоретические основы курса “Комплексные числа”§ 1 Развитие понятия числа, комплексные числа, алгебраическая форма, действия над комплексными числами, заданными в алгебраической форме. Комплексная плоскость. Геометрическая интерпретация комплексного числа, их суммы и разности.
При изучении математики мы уже неоднократно встречались с обобщением понятия числа. До сих пор мы рассматривали лишь действительные числа. Если введение действительных чисел позволяет выражать результаты любых измерений, то с задачей решения уравнений дело обстоит иначе. Например, уравнения ![]() х2 + 1=0 и х2 +4х +5=0 не имеют решения во множестве действительных чисел, хотя коэффициенты этих уравнений – целые числа. Поэтому возникает необходимость в дальнейшем расширении понятия числа. Таким обобщением множества действительных чисел и является множество С комплексных чисел.
х2 + 1=0 и х2 +4х +5=0 не имеют решения во множестве действительных чисел, хотя коэффициенты этих уравнений – целые числа. Поэтому возникает необходимость в дальнейшем расширении понятия числа. Таким обобщением множества действительных чисел и является множество С комплексных чисел.
Комплексные числа часто называют мнимыми. Это название не вполне удачно, т.к. может создать представление о комплексных числах как о чём-то нереальном. Оно объясняется тем, что, хотя комплексные числа стали употребляться ещё в XVI в., они долго продолжали казаться даже выдающимся математикам чем-то реально не существующим, мнимыми в буквальном смысле этого слова. Одному из создателей дифференциального и интегрального исчисления, немецкому математику Г.Лейбницу (1646-1716) принадлежат, например, такие слова: „Комплексное число – это тонкое и поразительное средство божественного духа, почти амфибия между бытием и небытием”. Сейчас от всей этой мистики не осталось ничего, кроме, пожалуй, названия “мнимые числа”. Уже во времена К.Гаусса (1777-1855) было дано геометрическое истолкование комплексных чисел как точек плоскости. Трудами выдающихся математиков XIX века О.Коши, Г.Римана и К.Вейерштрасса на базе комплексных чисел была построена одна из самых красивых математических дисциплин – теория функций комплексной переменной.
Повторить с учащимися известные им сведения о числовых множествах:
а) натуральных чисел N={1,2,3,…,n,…};
б) целых Z={…,-2,-1,0,1,2,…};
в) рациональных Q={m/n,n ![]() Z, n
Z, n ![]() N};
N};
г) действительных чисел R.
С помощью положительных действительных чисел можно выразить результат любого измерения, а с помощью произвольных действительных чисел – изменение любой величины. Арифметические операции над действительными числами снова дают действительные числа. Операция же извлечения квадратного корня определена не для всех действительных чисел, а лишь для неотрицательных – из отрицательного числа квадратный корень извлечь нельзя.
Ряд вопросов, возникших при решении уравнений третьей и четвертой степеней, привел математиков к необходимости расширить множество действительных чисел, присоединив к ним новое число i, такое, что i2=-1.Поскольку действительных чисел с таким свойством не существует, новое число назвали “мнимой единицей” – она не выражала ни результатов измерения величин, ни изменений этих величин. Но включение числа i потребовало дальнейшего расширения множества чисел – пришлось ввести произведение этого числа на все действительные числа, т.е. числа вида bi, где b![]() R, а также суммы действительных чисел и таких произведений, т.е. числа вида a+bi, где a,b
R, а также суммы действительных чисел и таких произведений, т.е. числа вида a+bi, где a,b![]() R. Получившиеся при этом числа были названы комплексными, т.к. они содержали как действительную часть a, так и чисто мнимую часть bi.
R. Получившиеся при этом числа были названы комплексными, т.к. они содержали как действительную часть a, так и чисто мнимую часть bi.
Опр: комплексными числами называются числа вида a+bi (a и b - действительные числа, i2=-1).
Если z=а+bi - комплексное число, то а называют его действительной частью, а b-мнимой частью. Приняты обозначения a=Re z, b=Jm z (от французских слов re¢ ele - действительный и imaginaire - мнимый). Числа a+bi, для которых b¹ 0, называют мнимыми числами, а числа вида bi, b¹ 0,- чисто мнимыми числами.
Множество комплексных чисел обозначается С.
Два комплексных числа z1=a+bi и z2=с+di считаются равными друг другу в том и только в том случае, если а=с и b=d. В частности, число a+bi будет считать равными нулю, если a=0 и b=0.
Запись z=a+bi называется алгебраической формой комплексного числа.
Действия над комплексными числами:
Сложение: (a+bi)+(c+di)=(a+c)+(b+d)iНапример , (2+3i)+(5-7i)=(2+5)+(3-7)i=7-4i.
Умножение: (a+bi)*(c+di)=(ac-bd)+(ad+bc)i , причем нужно помнить, что i2 =-1. Эту формулу можно получить, умножая(a+bi) на (c+di) по правилам действий над многочленами.
Например, (1+2i)(3-i) =3*1-1*i+6i-2i2 =3+2-i+6i=5+5i.
Рассмотрим степени числа i :
i1 =i ; i2 =-1; i3 =i2*i =-1*i =-i; i4 =i2*i2 =(-1)(-1) =1; i5=i3*i2=-i(-1)=i; i6= =i5*i=i*i=-1=i2; …
Вообщее, i4n+r =(i4)n*ir =(1)n *ir =ir.
Получаем, i4m=1; i4m+1=i; i4m+2=-1; i4m+3=-i.
Например, i218=i4*54+2=i2=-1.
Вычитание: (a+bi) - (c+di) = (a-c) + (b-d)iНапример, (5+4i) - (2-3i) = (5-2) + (4+3)i = 3+7i.
Опр: Два комплексных числа называются сопряженными, если они отличаются лишь знаком мнимой части.
Если z=a+bi, то сопряженное число имеет вид z=a-bi. Заметим, что z+z=(a+bi)+(a-bi)=2a; z*z=(a+bi)(a-bi)=a2+b2 . Следовательно, сумма и произведение двух сопряженных комплексных чисел являются действительными числами.
Деление: на практике при делении комплексных чисел удобно домножить числитель и знаменатель дроби на выражение, сопряженное знаменателю:(a+bi)/(c+di)=( (a+bi)(c-di))/((c-di)(c-di))=( (ac+bd)+(bc-ad)i)/(c2 + d2 )=( ac+bd)/(c2+d2 )+( bc-ad)/(c2+d2 )*i
Например, (10+15i)/(1+2i)=((10+15i)(1-2i))/((1+2i)(1-2i)) -( 10-20i +15i +30)/(1 + 4)=( 40-5i)/5= 8-i
Геометрическая интерпретация комплексных чисел.Как известно, действительные числа можно изображать точками на координатной прямой. А комплексное число естественно выражать точкой на координатной плоскости.
Каждому комплексному числу a+bi поставим в соответствии точку M(a;b) координатной плоскости, т.е. точку, абсцисса которой равна действительной части комплексного числа, а ордината - мнимой части. Каждой точке M(a; b) координатной плоскости поставим в соответствие комплексное число a+bi (рис.1).
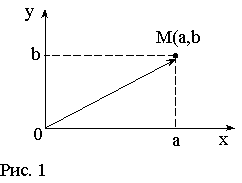
Очевидно, что получаемое при этом соответствие является взаимно однозначным. Сама координатная плоскость называется комплексной плоскостью. Действительным числам соответствуют точки оси абсцисс, которая называется действительной осью, а чисто мнимым числам - точки оси ординат, которая называется мнимой осью.
Не менее важной и удобной является интерпретация комплексного числа a+bi как радиус-вектора ОМ (см. рис.1), т.е. вектора, исходящего из начала координат О (о,о) и идущего в точку М (а;b). Разумеется, вместо радиус-вектора ОМ можно взять любой равный ему вектор.
Изображение комплексных чисел с помощью векторов удобно тем, что при этом получают простое геометрическое истолкование операций над ними. При сложении чисел z1=a1+b1i и z2=a2+b2i складываются их действительные и мнимые части. При сложении соответствующих им векторов ОМ1 и ОМ2 складываются их координаты. Иными словами, если числу z1 соответствует вектор ОМ1, а числу z1-вектор ОМ2, то числу z1+z2 соответствует вектор ОМ1+ОМ2, а числу z1-z2 - вектор ОМ1- ОМ2.
Перейдем к рассмотрению понятия модуля комплексного числа. Опр: Модулем комплексного числа называется длина вектора соответствующего этому числу.
Для модуля числа z используется обозначение /Z/ или r. По теореме Пифагора (см. рис.1) для модуля комплексного числа z=a+bi легко получается следующая важная формула: /Z/=Ö a2+b2, выражающая модуль числа через его действительную и мнимую части. Отмети, что /z/ = /-z/ = /z/, z*z = /z/2 = /z/2.
Упражнения:
(2Ö 3 - 4iÖ 2) - (Ö 27 - iÖ 32) + (2/Ö 3 + 2i/Ö 3 ) (m - n i)/n + ( n - m i - (( 1 - 1 i)/m - 1 - 1 i)/m)/n ; 2i (1/ /2+ Ö 3/2* i) ( -1/2+ Ö 3 /2*i ); Найдите комплексные числа:а) z =i + 6i+1 б) z = i13+ i14 + i15 +i16 ; в) z = 3+1 : 2
1+7i 3-i 5(1-i)
г) z = (1+2i)3 - (1-i)3 ; д) z = (2+i)5 е) z = 5+12i + (1+2i)2
(3+2i)3- (2+i)2 8-6i 2+i
ж) z = (-0,5 + i Ö 3/2) 3
Изобразить геометрически комплексные числа:а) 3+0i; б) 0-5i; в) -3+2i; г) 1+i.
Найдите действительную часть комплексного числа:z= (1+2i) + i19 ;
мнимую : z= (2-i)3 (2-11i).
Найти модуль к.ч. z= -2+ i*5, число, сопряженное данному, изобразить их геометрически.Выполнить сложение алгебраически и дать геометрическую интерпретацию: z= z1 +z2 +z3, где z1 = 3-2i; z2=-3+4i; z3 = 2- i. Найти два действительных числа Х и У, удовлет их равенствам:
а) (2i + iу -2 )/x=( 3i - 3)/x =у
б) (1+i)x + (1-i)у = 3-i;
в) (2x-3уi)(2x+3уi) +xi = 97+2i.
§2. Действия над комплексными числами, заданными
в алгебраической форме. Решение задач.
Провести комбинированный опрос. Фронтальный опрос провести по вопросам:
Обозначение числовых множеств и их соотношения. Почему появилась необходимость введения комплексных чисел? Определение комплексных чисел, частные случаи, основные соглашения. Определения сопряженных и противоположных комплексных чисел, модуля комплексного числа. Геометрическая интерпретация комплексных чисел, сопряженных и противоположных комплексных чисел. Действия над комплексными числами, заданными в алгебраической форме (определения и свойства). Действия над комплексными числами, геометрическая интерпретация их суммы и разности. Действия над сопряженными и противоположными комплексными числами (их сумму и разность показать геометрически). Можно ли сравнивать комплексные числа? Какие закономерности имеются у степени мнимой единицы.Индивидуальный опрос полезно провести по карточкам. Примерное содержание одного варианта:
Вычислить: а) (3+5i) + (2+i) = . . . . .; б) (3+5i) - (4-i) = . . . .; Возвести в степень: а) i123 = . . . ; б) (i-1)2 = . . . . Вычислить: (Ö 3 + iÖ 2) (Ö 3 - iÖ 2) = . . . . Построить слагаемые и сумму комплексных чисел на комплексной плоскости: z1=1-5i; z2=2+3i. Построить уменьшаемое, вычитаемое и разность комплексных чисел на комплексной плоскости: z1=1-i; z2=3i.Упражнения:
Выполнить действия: а) [2i (3-4i)]2 =; б) a-bi - i b-ai = ;в) i100 + i98 +i63 =;
Н основании равенства комплексных чисел, найти действительные числа Х и У, если а) 2+5i x - 3уi = 14i + 3x -5y; б) x2 -7x +9yx = y2i +20i -12.При каких действительных значениях Х и У комплексного числа
а) 5 + ixy и x + y +4i; б) 9y2 - 4 - 10x и 8y2 + 20i7 Будут сопряженными?
Решите уравнения: а) (i-z) (1+2i) + (2-iz) (3-4i) = 1+7i;б) z2 - (5+2i) z + 5 + 5i =0; в) z2 + z =0; г) (1-i) z - 3iz = 2-i; д) z*z + 2z =3+2i;
е) z*z + 3(z-z) - 4+3i.
Решите уравнения: а) /z/ = 2i (z+1); б) /z/ = i (2z+i); в) /z/ - iz = i-2i;г) z2 + 3/z/ =0; д) z2 + /z/2 =0.
Какое множество точек комплексной плоскости задается условием:а) /z/ <1; б) /z/ =2; в) Rez > 1; г) Jmz < -2; д) /z+i/ =2; е) /z-2/ <3; ж) /z-4 +i/ £ 5.
Точка А соответствует комплексному числу z = 3+ i4. Какое комплексное число соответствует точке симметричной точке А, относительно: а)оси Ох; б) оси Оу; в) начала координат? На комплексной плоскости даны точки z1, z2 , z3 являющиеся вершинами некоторого треугольника. Найдите все комплексные числа, соответствующие точками, дополняющим данный треугольник до параллелограмма. Изобразить: а) /z/ £ 3 б)/z/³ 1 в) /z-1/³ 2/z-3i/³ 3 /z-2i/£ 2 -1< Rez<2
г) 1£ /z-1/£ 2 д) /z/ £ 3
0£ Jmz£ Ö 3 1< Jmz <2.
§ 3 Тригонометрическая форма комплексного числа.
Переход от алгебраической формы комплексного числа к тригонометрической и обратно.
Повторить с учащимися алгебраическую форму комплексного числа; геометрическую интерпретацию комплексного числа; модуль комплексного числа и основные соотношения, связанные с ним.
Пусть точка А соответствует комплексному числу z=a+bi. Тогда длина вектора ОА называется модулем числа z, а радианная мера угла, образованного этим вектором с положительным направлением действительной оси, - аргументом комплексного числа Z. Причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если отсчет производится по часовой стрелке. Модуль обозначается /z/ = r, а аргумент - argz = j (см. рис. 2).
Для числа z=0 аргумент не определяется, но в этом и только в этом случае число задается только своим модулем. Если комплексное число является действительным, то соответствующий ему вектор расположен на действительной оси, и понятие /z/ совпадает с известным понятием модуля действительного числа.
Заданием модуля и аргумента комплексное число определяется однозначно. Но аргумент комплексного числа, в отличие от модуля, определяется не однозначно. Любые два аргумента комплексного числа отличаются друг от друга слагаемым, кратным 2p .
На рис. 2 мы видим, что sin j = b/r, а cos j =a/r, отсюда а=r cos j и b=r sin j , где r =Ö a2 + b2, т.о. действительная и мнимая части комплексного числа z=a+bi выражаются через его модуль /z/=r и аргумент j . Следовательно, комплексное число z может быть записано в виде z=r cos j + i r sin j =r(cos j +i sin j ) - тригонометрическая форма записи комплексного числа.
Полезно составить с учащимися алгоритм перехода из алгебраической формы комплексного числа в тригонометрическую:
Найти радиус r = Ö a2 + b2 Вычислить tg j 1 =|b/a|. По знакам a и b определить четверть, в которой находится число z.Найти j , причем, если число находится:
а) в I четверти, то j = j 1;
б) во II четверти, то j = p - j 1;
в) в III четверти, то j = p + j 1;
г) в IV четверти, то j = -j 1, или j = 2p -j 1.
Записать комплексное число в тригонометрической форме:z = r (cos j + i sin j ).
Или, чтобы не производить лишних вычислений, для того чтобы найти значение для j по известным значениям sin j и cos j , заполним таблицу и будем ею пользоваться:
| j | 0 | p 6 | p 4 | p 3 | p 2 | p | 5p 6 | 3p 4 | 2p 3 | 3p 2 | 4p 3 | 4p 4 | 7p 6 | 5p 3 | 7p 4 | 11p 6 | 2p |
| sinj | 0 | 1 2 | Ö 2 2 | Ö 3 2 | 1 | 0 | 1 2 | Ö 2 2 | Ö 3 2 | -1 | -Ö 3 2 | -Ö 2 2 | -1 2 | -Ö 3 2 | -Ö 2 2 | -1 2 | 0 |
| cosj | 1 | Ö 3 2 | Ö 2 2 | 1 2 | 0 | -1 | -Ö 3 2 | -Ö 2 2 | - 1 2 | 0 | -1 2 | -Ö 2 2 | -Ö 3 2 | 1 2 | Ö 2 2 | Ö 3 2 | 1 |
Переход от тригонометрической формы комплексного числа к алгебраической производится подстановкой в выражение z=r (cos j + i sin j ) числовых значений cos j и sin j , затем раскрываются скобки и производятся упрощения.
Например: 1) z = 1+i /z/ r =Ö 12+12 =Ö 2
sinj = 1/Ö 2 =2 cosj/2 = 1/Ö 2 = 2 Þ j = 450
т.о z = a + bi = 1 + i = Ö 2/4 (cos 450+ isin 450) =Ö 2/4 (cos p + sin p )
z = 6( cosp + isin p ) = 6 (-1 + i*0) = 6*-1 = -6 Þ z = -6.Упражнения:
Представьте в тригонометрической форме комплексные числа:а) Ö 3/2-i/2 ; б) 6+6i ; в) -2 ; г) i ; д) -1/7 - Ö 3/7 i е) -3 (cos p + isin p)
ж) sin 48° + cos 48° ; з) 1 + cos 10p /9+ isin 10p /9
Представьте в алгебраической форме комплексные числа :а) z = 2 (cos 225° + isin 225° ) ; б) z=3 (cos0° + isin 0° ) ;
в) z = 5(cos p/2 + isin p/2 ; г) z = 2(cos p/3 + isin p/3)
Построить комплексные числа? А) z=2 (cos p/4 + isin p/4 )б) z = cosp + isin p ; в) z =2 (cos 3p/4 + isin 3p/4)
Похожие работы
... поколения, поставленными обществом. Методика обучения математике призвана исследовать проблемы математического образования, обучения математике и математического воспитания. Методика преподавания математики в средней школе возникла с целью поиска педагогически целесообразных путей и способов изложения учебного материала. Методика преподавания математики начала разрабатываться чешским учёным ...
... уровня сформированности представлений о функциональной зависимости у младших школьников. 2 этап – формирующий этап - разработан и реализован комплекс упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников. 3 этап – контрольный этап - проведен анализ эффективности занятий с применением комплекса упражнений, направленных на формирование ...
... в процессе обучения, необходима разработка совершенно новых подходов к работе с таким видом информационных ресурсов как базы данных. Глава 2.Технология использования баз данных математических задач в процессе подготовки учащихся к ЕГЭ по математике 2.1 Реализация модели В соответствии с теорией поэтапного формирования умственных действий учащихся, подготовку к сдаче единого ...
... вероятностей совместимых событий; формулы: полной вероятности, Бейеса (Байеса). Одной из форм дифференцированного обучения по курсу теории вероятностей может являться факультативный курс. 2. Разработка программы факультативного курса по теории вероятностей в курсе математики 8 класса 2.1 Основные понятия о факультативном курсе Возможность 1-2 часа в неделю дополнительно работать со ...

0 комментариев