Алгебраическое сопряжение

4.2 Алгебраическое сопряжение

Определение. Алгебраическим сопряжением называется сопряжение, которое в сочетании с операцией умножения позволяет в любой алгебре получать действительное число. Как видим, различий относительно сопряжения по мнимой единице два - во-первых, отсутствует требование использования операции сложения и во-вторых в сочетании с произведением требуется получение числа именно алгебры действительных чисел, а не одной из предшествующих удвоению.

.

Или, алгебраическое сопряжение используется для определения модуля числа алгебры.

Для того, чтобы получить действительное число в случае произвольной гиперкомплексной алгебры, следует придумать процедуру, с помощью которой можно отбросить все мнимые единицы. Наиболее простой операцией сопряжения, при этом похожей на определенное выше сопряжение, является операция смены знаков сразу у всех мнимых единиц числа, безотносительно способа их получения и их свойств:

.

Сменив знаки при всех мнимых единицах, получим:

.

Естественно, что столь вольное обращение с мнимыми единицами не может гарантировать, что является действительным числом. Но при этом отметим, что сумма как раз является действительным числом. Таким образом, нам нужно отображение, которое произведению в одной области сопоставляет сложение в другой и наоборот. Такой операцией является пара отображений - логарифмирование и потенцирование. Еще раз напомним их свойства:

,

,

в случае, если a и b коммутируют по умножению.

Таким образом, для получения числа, алгебраически сопряженного заданному, нужно найти его логарифм, сменить знаки у всех мнимых единиц и потенцировать.

Любое число любой гиперкомплексной алгебры естественным образом коммутирует как само с собой, так и с действительным числом, поэтому

.

Или, если

, то .

Среди свойств алгебраического сопряжения отметим весьма важные:

- сопряженное произведения равно обратному произведению сопряженных:

,

,

- в некоторых алгебрах алгебраическое сопряжение совпадает по результату с сопряжением по действительных чисел, все виды сопряжения в ней совпадают. Сопряжение по мнимой единице:

.

a) Алгебраическое сопряжение:

;

,

то есть смена знаков мнимых единиц после логарифмирования эквивалентна смене знака у мнимой единицы самого числа:

.

Здесь одинаково обозначены сопряжение по мнимой единице и алгебраическое. Полагаю, пока нет совмещения сопряжений в одной формуле, разночтений возникнуть не должно.

б) кватернионы.

Кватернионы имеют строение:

и получены некоммутативным удвоением алгебры комплексных чисел:

.

Мнимая единица удвоения j не коммутирует с единицей i, поэтому сопряжение по ней требует сопряжения также и по i и по k:

.

Алгебраическое сопряжение в кватернионах, также как в комплексных числах, просто меняет знак у компонент при мнимых единицах:

.

То есть в кватернионах сопряжение по мнимой единице и алгебраическое сопряжение так же совпадают.

§5 .Некоторые тождества для октав

Приведем основные тождества, применимые к октавам. Тождества базируются на понятии ассоциатора, коммутатора и йорданова произведения.

()=- ассоциатор;

- коммутатор;

- йорданово произведение.

Линеаризуя тождества, несложно получить, что

& .

Таким образом, ассоциатор есть кососимметрическая функция от x, y, z. В частности:.

.

Алгебры, удовлетворяющие этому условию, называются эластичными. Таким образом, алгебра октав эластична. Покажем на основе эластичности тождество:

,

.

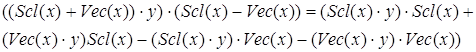В силу того, что  для октав всегда есть действительное число, а в силу эластичности,  получаем:

.

Таким образом, для эластичной алгебры справедливо:

.

Функция Клейнфелд:

.

Лемма1. - кососимметрическая, для любой пары равных аргументов

.

В силу правой альтернативности

.

Во всякой алгебре справедливо тождество:

.

Достаточно раскрыть все ассоциаторы. Обозначив левую часть этого равенства через , получим:

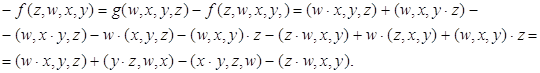
Поменяв местами: получим: .

Используя , получим, что при любых одинаковых аргументах. Из этого следуют тождества:

1) ;

2) ;

3) ;

4) .

Тождества Муфанг.

Правое тождество Муфанг: ;

Левое тождество Муфанг: ;

Центральное тождество Муфанг: .

Вопросы о строении простых алгебр в том или ином многообразии являются одними из главных вопросов теории колец. Мы уже знаем один пример простой неассоциативной альтернативной алгебры - это алгебра Кэли-Диксона. Оказывается, что других простых неассоциативных альтернативных алгебр не существует. Этот результат доказывался с нарастанием общности на протяжении нескольких десятков лет разными авторами: вначале для конечномерных алгебр (Цорн, Шафер), затем для алгебр с нетривиальным идемпотентом (Алберт), для альтернативных тел (Брак, Клейнфелд, Скорнаков), для коммутативных альтернативных алгебр (Жевлаков) и т. д. Наибольшее продвижение было получено Клейнфелдом, доказавшим, что всякая простая альтернативная неассоциативная алгебра, не являющаяся ниль-алгеброй характеристики 3, есть алгебра Кэли-Диксона. Окончательное описание простых альтернативных алгебр осуществилось после появления теоремы Ширшова о локальной нильпонентности альтернативных ниль-алгебр с тождественными соотношениями.

§6. Теорема Гурвица