Навигация
Построение частотных характеристик (АЧХ, ФЧХ) системы, ЛАЧХ разомкнутой системы, переходной характеристики
2. Построение частотных характеристик (АЧХ, ФЧХ) системы, ЛАЧХ разомкнутой системы, переходной характеристики
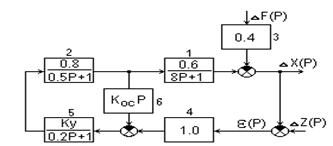
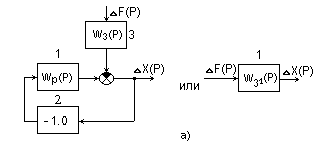
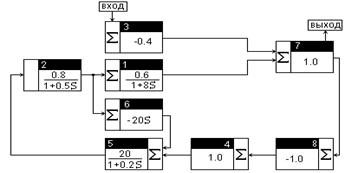
На рис.3 показана модель замкнутой системы. Чтобы построить характеристику для разомкнутой системы (кривую Найквиста), необходимо разорвать главную обратную связь (рис.5).
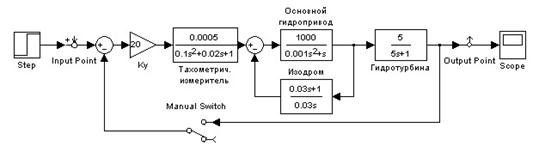
Рис. 5. Модель разомкнутой САУ, составленная в MATLAB / SIMULINK
Имея модель САУ в SIMULINK, легко построить её частотные и переходную характеристики с помощью другого инструмента: LTI Viewer. Он предназначен для анализа линейных стационарных систем. С помощью данного инструмента можно построить частотные характеристики исследуемой системы, получить её отклики на единичные ступенчатое и импульсное воздействия, построить годограф Найквиста и т.д.
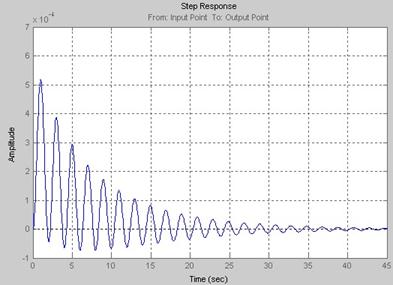
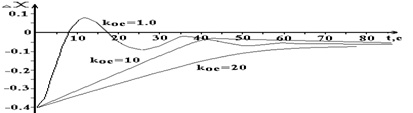
Рис. 5. Переходный процесс САУ
Для построения амплитудно-частотной характеристики (АЧХ) замкнутой системы производят подстановку ![]() в выражение для передаточной функции замкнутой системы
в выражение для передаточной функции замкнутой системы ![]() и АЧХ строят по выражению:
и АЧХ строят по выражению: ![]() .
.
Фазо-частотная характеристика (ФЧХ) замкнутой системы строится по выражению:
![]() ,
,
т. е. как аргумент комплексной передаточной функции замкнутой системы. ![]() ,
, ![]() - соответственно действительная и мнимая части комплексной передаточной функции замкнутой системы
- соответственно действительная и мнимая части комплексной передаточной функции замкнутой системы ![]() .
.
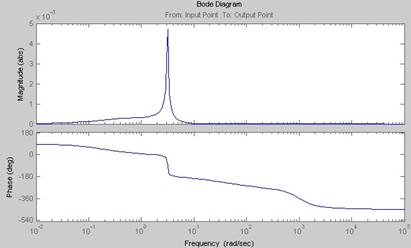
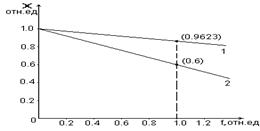
Рис. 6. АЧХ и ФЧХ замкнутой системы
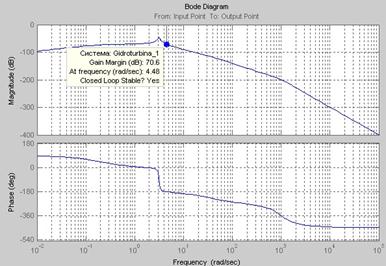
Рис. 7. Логарифмические частотные характеристики разомкнутой САУ
3. Исследование системы на устойчивость
Критерий Гурвица
Характеристическое уравнение замкнутой системы в общем виде имеет вид:
![]() (91)
(91)
Составим определители Гурвица:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
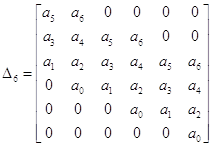 ;
; 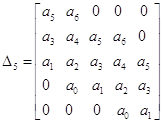 ;
; 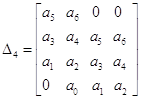 ;
;
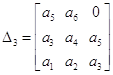 ;
; 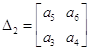 ;
; ![]() .
.
Программа анализа устойчивости САУ:
% Анализ устойчивости САУ по Гурвицу
% Коэффициенты характеристического уравнения замкнутой системы:
a7=75;
a6=75030;
a5=75030753;
a4=2530753150;
a3=1753150000;
a2=254*1.0e+8;
a1=5*1.0e+9;
% a - вектор коэффициентов характеристического уравнения замкнутой системы
% a(7)*p^6+a(6)*p^5+a(5)*p^4+a(4)*p^3+a(3)*p^2+a(2)*p^1+a(1)
% нумерация начинается с единицы, а не с нуля
a = [a1 a2 a3 a4 a5 a6 a7];
disp('Вычисление определителей Гурвица:');
A6=[a(6) a(7) 0 0 0 0; a(4) a(5) a(6) a(7) 0 0; a(2) a(3) a(4) a(5) a(6) a(7);
0 a(1) a(2) a(3) a(4) a(5); 0 0 0 a(1) a(2) a(3); 0 0 0 0 0 a(1)]
d6=det(A6)
A5=[a(6) a(7) 0 0 0; a(4) a(5) a(6) a(7) 0; a(2) a(3) a(4) a(5) a(6);
0 a(1) a(2) a(3) a(4); 0 0 0 a(1) a(2)]
d5=det(A5)
A4=[a(6) a(7) 0 0; a(4) a(5) a(6) a(7); a(2) a(3) a(4) a(5); 0 a(1) a(2) a(3)]
d4=det(A4)
A3=[a(6) a(7) 0; a(4) a(5) a(6); a(2) a(3) a(4)]
d3=det(A3)
A2=[a(6) a(7); a(4) a(5)]
d2=det(A2)
A1=[a(6)]
d1=det(A1)
if d6>0 && d5>0 && d4>0 && d3>0 && d2>0 && d1>0
s='Так как все определители Гурвица больше нуля, то система УСТОЙЧИВА';
else
s='Так как не все определители Гурвица положительны, то система НЕ УСТОЙЧИВА';
end
disp(s);
Результат работы программы:
>> Вычисление определителей Гурвица:
A6 = 1.0e+010 *
0.0000 0.0000 0 0 0 0
0.2531 0.0075 0.0000 0.0000 0 0
2.5400 0.1753 0.2531 0.0075 0.0000 0.0000
0 0.5000 2.5400 0.1753 0.2531 0.0075
0 0 0 0.5000 2.5400 0.1753
0 0 0 0 0 0.5000
d6 = 8.7654e+050
A5 = 1.0e+010 *
0.0000 0.0000 0 0 0
0.2531 0.0075 0.0000 0.0000 0
2.5400 0.1753 0.2531 0.0075 0.0000
0 0.5000 2.5400 0.1753 0.2531
0 0 0 0.5000 2.5400
d5 = 1.7531e+041
A4 = 1.0e+010 *
0.0000 0.0000 0 0
0.2531 0.0075 0.0000 0.0000
2.5400 0.1753 0.2531 0.0075
0 0.5000 2.5400 0.1753
d4 = 1.3753e+031
A3 = 1.0e+010 *
0.0000 0.0000 0
0.2531 0.0075 0.0000
2.5400 0.1753 0.2531
d3 = 1.3757e+022
A2 = 1.0e+009 *
0.0001 0.0000
2.5308 0.0750
d2 = 5.4398e+012
A1 = 75030
d1 = 75030
Так как все определители Гурвица больше нуля, то система УСТОЙЧИВА.
Критерий Михайлова
Построим годограф Михайлова – кривую, которая описывается характеристическим вектором на комплексной плоскости. Характеристический вектор получим, подставив ![]() в характеристический полином (знаменатель передаточной функции замкнутой системы):
в характеристический полином (знаменатель передаточной функции замкнутой системы):
![]()
Программа анализа устойчивости САУ:
disp (' *** Анализ устойчивости по критерию Михайлова ***');
% знаменатель характеристического уравнения замкнутой системы
% a(7)*p^6+a(6)*p^5+a(5)*p^4+a(4)*p^3+a(3)*p^2+a(2)*p^1+a(1), где вектор a найден ранее
for i=1:1101
w(i)=i-1;% вектор значений частот
end
N=length(w);
for k=1:N
M(k)=-a(7)*w(k)^6+a(6)*j*w(k)^5+a(5)*w(k)^4-a(4)*j*w(k)^3-a(3)*w(k)^2+a(2)*j*w(k)+a(1);
end
x=real(M); % действительная часть
y=imag(M); % мнимая часть
plot(x,y); grid on;
В результате получаем график (рис. 8,а,б).
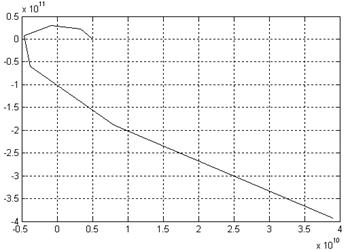
а)
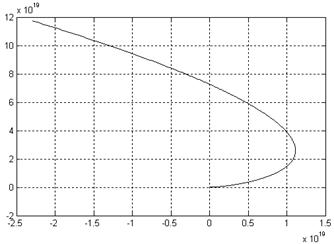
б)
Рис.8. Кривая Михайлова: а) ![]() , б)
, б) ![]()
Характеристический полином имеет степень 6-го порядка, следовательно, для устойчивости данной системы необходимо, чтобы характеристический вектор описывал угол ![]() , т.е. последовательно проходил шесть квадрантов комплексной плоскости. Так как это условие выполняется, то система является устойчивой.
, т.е. последовательно проходил шесть квадрантов комплексной плоскости. Так как это условие выполняется, то система является устойчивой.
Критерий Найквиста
Критерий Найквиста позволяет судить об устойчивости замкнутой системы по виду амплитудно-фазовой характеристики (АФЧХ) разомкнутой системы.
АФЧХ разомкнутой системы, строим в программе MATLAB/SIMULINK с помощью инструмента LTI Viewer.
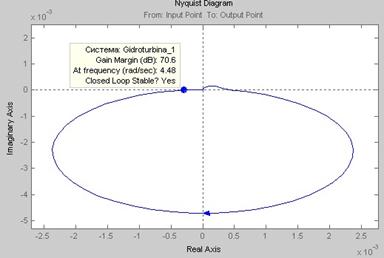
Рис.9. АФЧХ (кривая Найквиста) разомкнутой системы
Так как кривая Найквиста не охватывает точку (-1;i0), то система является устойчивой.
Запасы устойчивости
Запасы устойчивости определим графически по ЛЧХ разомкнутой системы (рис.7).
![]()
Запас устойчивости по амплитуде ![]() .
.
По определению частота среза ![]() - это частота, при которой АФЧХ пересекает окружность единичного радиуса с центром в точке (0;i0). Но, так как кривая Найквиста расположена внутри единичной окружности (рис.9) и не пересекает её, то частота среза отсутствует. Откуда следует, что фаза может изменяться в любых пределах без риска для устойчивости системы.
- это частота, при которой АФЧХ пересекает окружность единичного радиуса с центром в точке (0;i0). Но, так как кривая Найквиста расположена внутри единичной окружности (рис.9) и не пересекает её, то частота среза отсутствует. Откуда следует, что фаза может изменяться в любых пределах без риска для устойчивости системы.
Вывод: система устойчива.
Похожие работы
... поведение регулируемой величины. Управляющее воздействие вырабатывается устройством управления (УУ). Совокупность взаимодействующих управляющего устройства и управляемого объекта образует систему автоматического управления. Система автоматического управления (САУ) поддерживает или улучшает функционирование управляемого объекта. В ряде случаев вспомогательные для САУ операции (пуск, остановка, ...
... ЛСАУ. ЦСАУЧМ – централизованная САУ частотой и мощностью; ЦСАУН -- централизованная САУ напряжением (управл. U и Q) В состав автоматизированного технологического управления эл. эн. системы кроме автоматизированных систем управления входят и автоматические системы управления. Есть 2 группы таких систем: САУ нормальным и САУ аварийным режимами (Н.Р. и А.Р,). Устойчивость параллельной работы ...
... приведены краткие выводы о свойствах исследуемой системы, числовые значения показателей качества управления, их оценка и, по возможности, рекомендации по их улучшению. ЛИТЕРАТУРА 1. Коротков В.Ф. Основы линейной теории автоматического управления в задачах электроэнергетики: Учебное пособие с компьютерным лабораторным практикумом АОС - ТАУ / Иван. Гос. Энерг. ун-т. - Иваново, 1994. - 392 с. ...
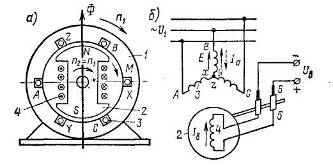
... особенностью машины постоянного тока является наличие коллектора и скользящего контакта между обмоткой якоря и внешней электрической цепью. 2.2 Устройство машины постоянного тока Машина постоянного тока (рис. 2.3) по конструктивному исполнению подобна обращенной синхронной машине, у которой обмотка якоря расположена на роторе, а обмотка возбуждения – на статоре. Основное отличие заключается ...


0 комментариев