Навигация
Определить алгебраические дополнения элементов 2-й строки определителя 3-го порядка
2. Определить алгебраические дополнения элементов 2-й строки определителя 3-го порядка.
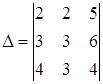
Для элемента а21 i=2, j=1 и i+j=3 число нечетное, отсюда ![]()
Для элемента а22 i=2, j=2 и i+j=4 число четное, отсюда ![]()
Для элемента а23 i=2, j=3 и i+j=5 число нечетное, отсюда ![]()
3. Найти решение системы уравнений методом Крамера.

Данная система уравнений будет иметь единственное решение только тогда, когда определитель составленный из коэффициентов при X1 - n не будет равен нулю. Обозначим этот определитель знаком - Δ. Если этот определитель не равен нулю, то решаем дальше. Тогда каждый Xi = Δi / Δ, где Δi - это определитель составленный из коэффициентов при X1 - n, только значения коэффициентов в i - ом столбце заменены на значения за знаком равенства в системе уравнений, а Δ - это главный определитель
Решение:
Запишем систему в виде:
Главный определить
4. Выполните операцию произведения двух матриц АхВ.
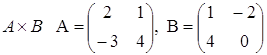
Решение:
Найти матрицу |C| = |A| x |B|
Вычислим элементы матрицы |C|:
c1,1 = a1,1b1,1+a1,2b2,1
c1,2 = a1,1b1,2+a1,2b2,2
c2,1 = a2,1b1,1+a2,2b2,1
c2,2 = a2,1b1,2+a2,2b2,2
| c1,1 = | 2 | * | 1 | + | 1 | * | 4 | = | 2 | + | 4 | = | 6 |
| c1,2 = | 2 | * | -2 | + | 1 | * | 0 | = | -4 | + | 0 | = | -4 |
| c2,1 = | -3 | * | 1 | + | 4 | * | 4 | = | -3 | + | 16 | = | 13 |
| c2,2 = | -3 | * | -2 | + | 4 | * | 0 | = | 6 | + | 0 | = | 6 |
Результирующая матрица |С|:
| 6 | -4 |
| 13 | 6 |
1 семестр 2 кредит
1. Какие величины называются скалярными и векторными? Приведите примеры скалярных и векторных величин? Каково условие равенства векторов? Приведите пример сложения двух векторов по правилу параллелограмма и треугольника.
Скалярной величиной или просто скаляром называется величина, которая при определённом выборе единицы измерения определяется числом (удельный вес, плотность, работа, мощность, температура и т.д.)
Вектор - направленный отрезок, имеющий определённую величину (скорость, ускорение, сила, напряженность магнитного и электрического поля и т.д.).
Скалярная величина - 10 минут, векторная - 100 км/ч.
Два вектора ![]() и
и ![]() равны, если они равнонаправлены и имеют один и тот же модуль.
равны, если они равнонаправлены и имеют один и тот же модуль.
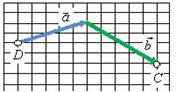
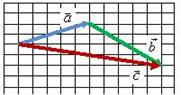
Правило треугольника.
Для того чтобы сложить два вектора ![]() и
и ![]() нужно переместить вектор
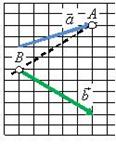
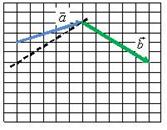
нужно переместить вектор ![]() параллельно самому себе (рис.1, б) так, чтобы его начало (точка B на рис.1, а) совпадало с концом вектора
параллельно самому себе (рис.1, б) так, чтобы его начало (точка B на рис.1, а) совпадало с концом вектора ![]() (точка A на рис.1, а). Тогда их суммой будет вектор
(точка A на рис.1, а). Тогда их суммой будет вектор ![]() (рис.1, г), начало которого совпадает с началом вектора
(рис.1, г), начало которого совпадает с началом вектора ![]() (точка D на рис.1, в), а конец - с концом вектора
(точка D на рис.1, в), а конец - с концом вектора ![]() (точка C на рис.1, в).
(точка C на рис.1, в).
а б
в г
Рис.1.
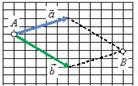
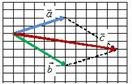
Правило параллелограмма.
Для того чтобы сложить два вектора ![]() и
и ![]() нужно переместить их параллельно самим себе так, чтобы начала векторов
нужно переместить их параллельно самим себе так, чтобы начала векторов ![]() и
и ![]() находились в одной точке (рис.2, а). Затем построить параллелограмм, сторонами которого будут эти вектора (рис.2, б). Тогда их суммой будет вектор
находились в одной точке (рис.2, а). Затем построить параллелограмм, сторонами которого будут эти вектора (рис.2, б). Тогда их суммой будет вектор ![]() (рис.2, в), начало которого совпадает с общим началом векторов (точка A на рис.2, б), а конец - с противоположной вершиной параллелограмма (точка В на рис.2, б).
(рис.2, в), начало которого совпадает с общим началом векторов (точка A на рис.2, б), а конец - с противоположной вершиной параллелограмма (точка В на рис.2, б).

а
б в
Рис.2.
Похожие работы
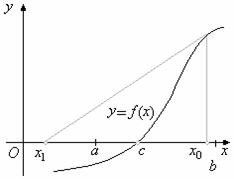
... - в методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики ...
... решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n - ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с ...
... «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных ...
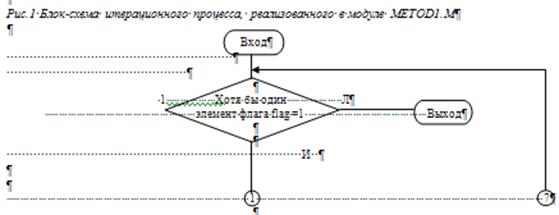
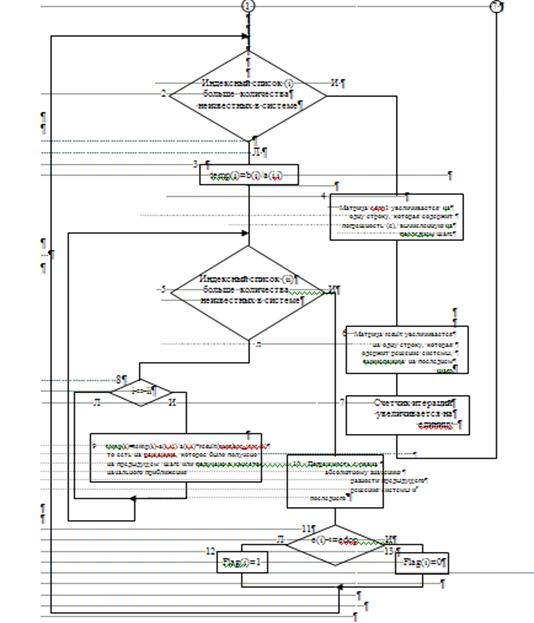
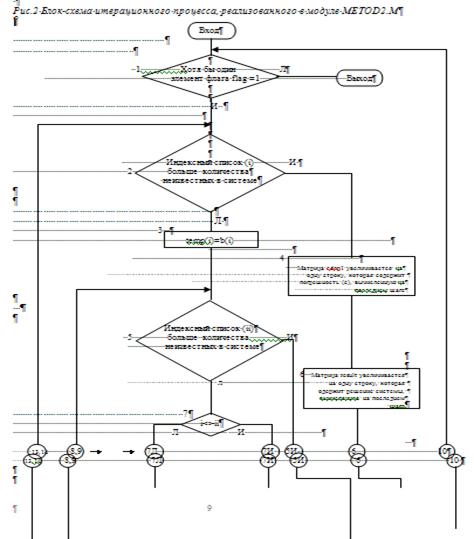
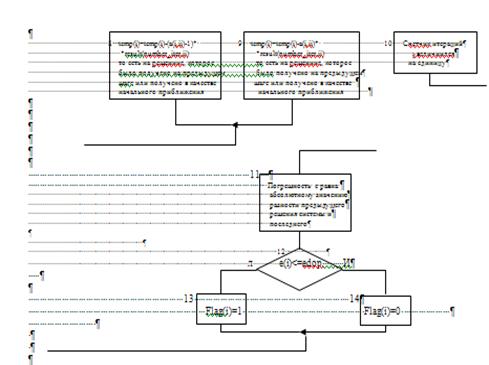
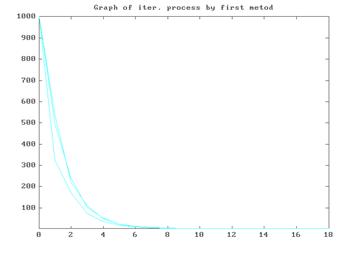
... , но выбор перехода к системе x=(x) зависит от типа конкретной решаемой системы линейных алгебраических уравнений. 6. Заключение В данной курсовой работе был реализован метод простой итерации для решения систем линейных алгебраических уравнений в виде двух программ, каждая из которых использует свой собственный способ перехода от системы вида F(x)=x к системе вида x=(x). Вообще говоря, ...
0 комментариев