Навигация
Напишите формулу разложения вектора по трем взаимно перпендикулярным осям координат
2. Напишите формулу разложения вектора по трем взаимно перпендикулярным осям координат.
![]()
3. Как определяется вектор через координаты его начала и конца?
Пусть известны координаты начала вектора А (x1, y1, z1) и его конца В (x2, y2, z2). Точки А и В определяют радиус вектора
|
 |
рис. 3
Из треугольника ОАВ следует, что ![]() , отсюда
, отсюда ![]() .
.
Если обозначить через X, Y, Z - координаты вектора ![]() , т.е.
, т.е. ![]() = (X, Y, Z), то следует, что
= (X, Y, Z), то следует, что
X=х2-х1
Y=у2-у1
Z=z2-z1
Чтобы найти абсциссу вектора Х, необходимо из абсциссы конца вектора вычесть абсциссу начала вектора.
3. Какой вид имеет уравнение прямой в плоскости, проходящей через две точки?
![]()
4. Какой вид имеет уравнение прямой с угловым коэффициентом?
![]()
2 уровень
1. Напишите разложение вектора по трем взаимно перпендикулярным осям координат.
| Координаты вектора | X | -2 |
| Y | 4 | |
| Z | 7 |
A (-2, 4,7) означает, что абсцисса точки A x=-2, ордината у=4, аппликата z=7.
2. Чему равно скалярное произведение векторов ![]()
![]() и
и ![]() ? Данные для варианта взять из таблицы 2.3
? Данные для варианта взять из таблицы 2.3
| Координаты вектора | X | -2 |
| Y | 4 | |
| Z | 7 | |
| Координаты вектора | X | 3 |
| Y | 6 | |
| Z | 4 |
Т.к. векторы заданы в координатной форме, то по формуле
![]()
имеем:
![]()
3. Найти уравнение прямой, проходящей через точку пересечения прямых l1 и l2 и отсекающей на оси абсцисс отрезок, равный d.
| Уравнение прямой l1 | Уравнение прямой l2 | d | Координаты точки Р | |
| x | y | |||
| 3x-2y-7=0 | x+3y-6=0 | 3 | 2 | 5 |
![]()
Отсюда находим х = 6 - 3у

x = 3
Значит точка пересечения двух прямых A (3;1)
По условия отрезок равен 3, значит координата точки B (3; 0).
Найдем уравнение прямой, проходящей через точки А и В.
![]()
![]()
Здесь знаменатель равен нулю. Полагаем числитель левой части равным нулю.
Получаем ![]()
4. Найти уравнение прямой, отсекающей на оси ординат отрезок, равный d и проходящей параллельно прямой l1.
| Уравнение прямой l1 | Уравнение прямой l2 | d | Координаты точки Р | |
| x | y | |||
| 3x-2y-7=0 | x+3y-6=0 | 3 | 2 | 5 |
Найдем две точки прямой 3x-2y-7=0
Подставим в уравнение х=1 и х=3 и получим значения у соответственно - 2 и 1.
A (1; - 2) и B (3;1).
Координаты направляющего вектора ![]() найдём по координатам конца и начала вектора
найдём по координатам конца и начала вектора
![]()
![]()
![]()
Подставляя в формулу
![]()
координаты точки O (0;3)
И координаты вектора ![]() получим искомое уравнение прямой
получим искомое уравнение прямой
![]() или
или ![]() .
.
2 семестр 4 кредит 1 уровень.
1. Как определяются горизонтальные асимптоты функции?
В случае, если наклонная асимптота расположена горизонтально, то есть при ![]() , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота - частный случай наклонной асимптоты; прямая y = с = const является горизонтальной асимптотой графика y = f (x) при
, она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота - частный случай наклонной асимптоты; прямая y = с = const является горизонтальной асимптотой графика y = f (x) при ![]() или
или ![]() , если
, если
![]()
Или
![]()
соответственно.
2. Что такое частное приращение функции нескольких переменных?
Частной производной функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных ![]() в точке
в точке ![]() частные производные определяются так:
частные производные определяются так:
![]() ,
,
![]() ,
,
если эти пределы существуют.
Из определения следует геометрический смысл частной производной функции двух переменных: частная производная ![]() - угловой коэффициент касательной к линии пересечения поверхности
- угловой коэффициент касательной к линии пересечения поверхности ![]() и плоскости
и плоскости ![]()
![]() в соответствующей точке.
в соответствующей точке.
3. Каковы выражения для частных дифференциалов функции z=f (x,y)?
Частной производной по x функции z = f (x,y) в точке M0 (x0,y0) называется предел 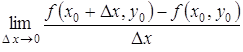 ,
,
если этот предел существует. Обозначается эта частная производная любым из следующих символов:
![]() ;
; ![]() ;
; 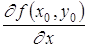 .
.
Частная производная по x есть обычная производная от функции z = f (x,y), рассматриваемой как функция только от переменной x при фиксированном значении переменной y.
Совершенно аналогично можно определить частную производную по y функции z = f (x,y) в точке M0 (x0,y0):
 =
= .
.
Приведем примеры вычисления частных производных/
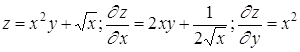
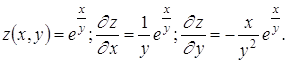
4. Каково выражение для полного дифференциала функции u=u (x,y,z)?
Полный дифференциал du функции u = f (x,y,z) (если он существует) равен сумме всех ее частных дифференциалов:
![]()
5. Напишите частные производные третьего порядка для функции z=f (x,y,z).


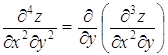
2 уровень
1. Найти частную производную и частный дифференциал функции.
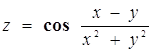
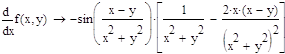
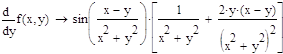
2. Вычислить значения частных производных f’x (M0), f’y (M0), f’z (M0) для данной функции f (x,y,z) в точке M0 (x0,y0,z0) с точностью до двух знаков после запятой.

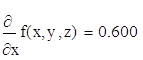


3. Вычислить значения частных производных функции z (x,y), заданной неявно, в данной точке M0 (x0,y0,z0) с точностью до двух знаков после запятой.
lnZ=x+2y-z+ln3 M0 (1,1,3)
![]()
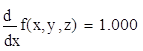
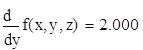
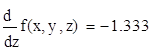
4. Найти уравнение касательной плоскости и нормали к заданной поверхности S в точке M0 (x0,y0,z0). S: z=x2+y2-4xy+3x-15, M0 (-1,3,4)
![]()
![]()
![]()
![]()
Следовательно, уравнение касательной плоскости будет таким:
![]()
![]()
а уравнение нормали таким:
![]()
Похожие работы
... - в методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики ...
... решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n - ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с ...
... «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных ...
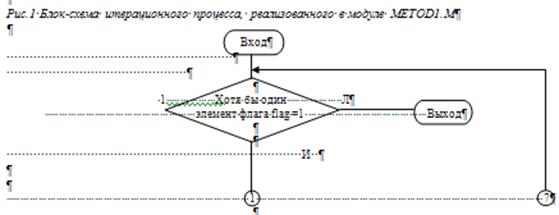
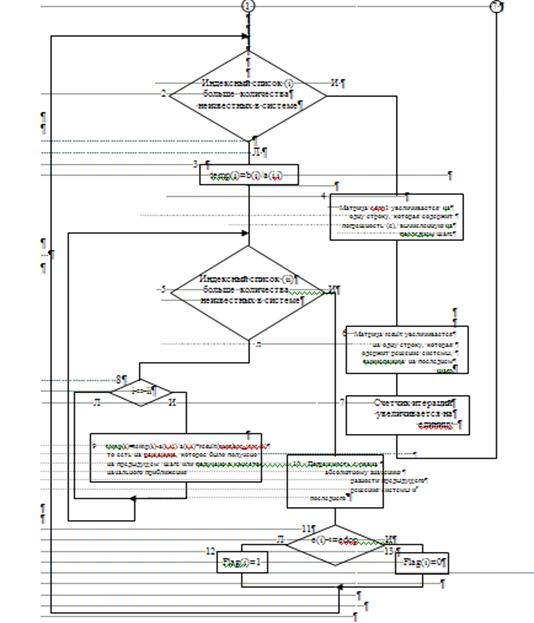
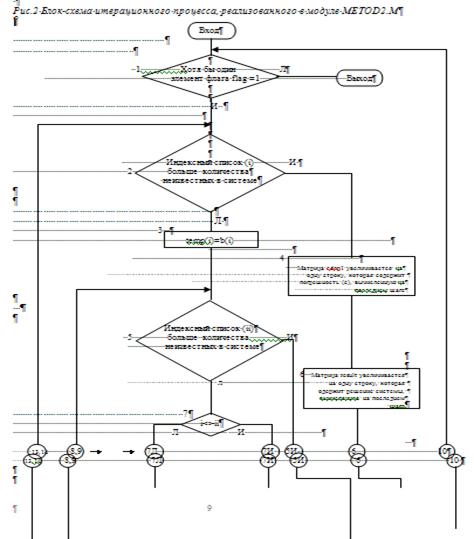
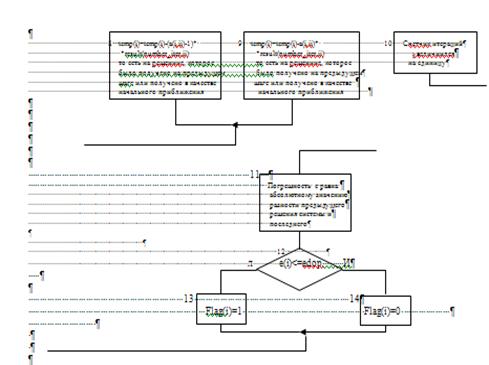
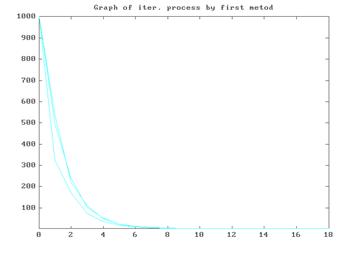
... , но выбор перехода к системе x=(x) зависит от типа конкретной решаемой системы линейных алгебраических уравнений. 6. Заключение В данной курсовой работе был реализован метод простой итерации для решения систем линейных алгебраических уравнений в виде двух программ, каждая из которых использует свой собственный способ перехода от системы вида F(x)=x к системе вида x=(x). Вообще говоря, ...
0 комментариев