Навигация
3. Муравей
Муравей - это программный агент, который является членом большой колонии и используется для решения какой-либо проблемы. Муравей снабжается набором простых правил, которые позволяют ему выбирать путь в графе. Он поддерживает список узлов, которые он уже посетил. Таким образом, муравей должен проходить через каждый узел только один раз. Путь между двумя узлами графа, по которому муравей посетил каждый узел только один раз, называется путем Гамильтона, по имени математика сэра Уильяма Гамильтона.
Узлы в списке "текущего путешествия" располагаются в том порядке, в котором муравей посещал их. Позже список используется для определения протяженности пути между узлами. Настоящий муравей во время перемещения по пути будет оставлять за собой феромоны. В алгоритме муравья агент оставляет феромоны на ребрах графа после завершения путешествия.
Стартовая точка, куда помещается муравей, зависит от ограничений, накладываемых условиями задачи, так как для каждой задачи способ размещения муравьев является определяющим. Либо все они помещаются в одну точку, либо в разные с повторениями, либо без повторений.
На этом же этапе задается начальный уровень феромона. Он инициализируется небольшим положительным числом для того, чтобы на начальном шаге вероятности перехода в следующую вершину не были нулевыми.
4. Начальная популяция
После создания популяция муравьев поровну распределяется по узлам сети. Необходимо равное разделение муравьев между узлами, чтобы все узлы имели одинаковые шансы стать отправной точкой. Если все муравьи начнут движение из одной точки, это будет означать, что данная точка является оптимальной для старта, а на самом деле мы этого не знаем.
5. Движение муравья
Движение муравья основывается на одном и очень простом вероятностном уравнении. Если муравей еще не закончил путь, то есть не посетил все узлы сети, для определения следующей грани пути используется уравнение :
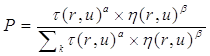
(2.1)
Здесь 
- интенсивность фермента на грани между узлами r и u, -Функция, которая представляет измерение обратного расстояния для грани, a -вес фермента, а b- коэффициент эвристики. Параметры a и b определяют относительную значимость двух параметров, а также их влияние на уравнение. Вспомните, что муравей путешествует только по узлам, которые еще не были посещены (как указано списком табу). Поэтому вероятность рассчитывается только для граней, которые ведут к еще не посещенным узлам. Переменная k представляет грани, которые еще не были посещены.
6. Путешествие муравья
Пройденный муравьем путь отображается, когда муравей посетит все узлы диаграммы. Обратите внимание, что циклы запрещены, поскольку в алгоритм включен список табу. После завершения длина пути может быть подсчитана - она равна сумме всех граней, по которым путешествовал муравей. Уравнение показывает количество фермента, который был оставлен на каждой грани пути для муравья k. Переменная Q, является константой.
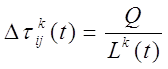(2.2)
Результат уравнения является средством измерения пути, - короткий путь характеризуется высокой концентрацией фермента, а более длинный путь - более низкой. Затем полученный результат используется в уравнении 2.3, чтобы увеличить количество фермента вдоль каждой грани пройденного муравьем пути.
(2.3)
Обратите внимание, что данное уравнение применяется ко всему пути, при этом каждая грань помечается ферментом пропорционально длине пути. Поэтому следует дождаться, пока муравей закончит путешествие и только потом обновить уровни фермента, в противном случае истинная длина пути останется неизвестной. Константа р - значение между 0 и 1.
7. Испарение фермента
В начале пути у каждой грани есть шанс быть выбранной. Чтобы постепенно удалить грани, которые входят в худшие пути в сети, ко всем граням применяется процедура испарения фермента. Используя константу р из уравнения 2.3, мы получаем уравнение 2.4.
(2.4)
Поэтому для испарения фермента используется обратный коэффициент обновления пути.
8. Повторный запуск
После того как путь муравья завершен, грани обновлены в соответствии с длиной пути и произошло испарение фермента на всех гранях, алгоритм запускается повторно. Список табу очищается, и длина пути обнуляется. Муравьям разрешается перемещаться по сети, основывая выбор грани на уравнении 2.1. Этот процесс может выполняться для постоянного количества путей или до момента, когда на протяжении нескольких запусков не было отмечено повторных изменений. Затем определяется лучший путь, который и является решением.
Похожие работы
... казалось принципиально невозможным. Очевидно, что эксперимент, опирающийся на традиционные способы поиска электромагнитных сигналов, не смог бы обнаружить этот канал. Почему же нельзя предположить, что распределенный мозг использует какой-то неизвестный нам способ передачи информации по каналу электромагнитных колебаний? С другой стороны, в повседневной жизни можно найти примеры передачи ...
... , 2004. – 382 с. 2. Инновационный менеджмент: Учеб. пособие / Под ред. В.М. Аньшина, А.А. Дагаева. – М.: Дело, 2003.- 528 с. Темы 12. Финансирование в инновационном менеджменте Лекция № 16 (к.т.н. Старовойтенко О.А.) План 12.1.Организационно - экономическое стимулирование нововведений. 12.2.Финансирование и кредитование нововведений. 12.3. Модели рынка нововведений и научно- ...
... системы развивающего обучения - свойства вариантности, учитывающего прежде всего индивидуальные особенности школьников. самоконтроль школьник тестовый орфографический Глава 3. Опытно-экспериментальная работа по формированию навыков орфографического самоконтроля у младших школьников на уроках русского языка Опытно-экспериментальная работа по проверке теоретически выделенных методов и ...
змы по-прежнему превосходили электронные, нам придётся поискать способ объединить компьютеры и человеческий мозг, либо попытаться искусственным путём усовершенствовать собственные гены. (Подробнее об этом рассказывается здесь) Впрочем, такие проекты пока остаются фантастикой. До их реализации пока ещё очень далеко, а пока главным предназначением устройств, подобных созданной в Мюнхене нейросхеме, ...
0 комментариев