Навигация
9 Блок-схема алгоритма
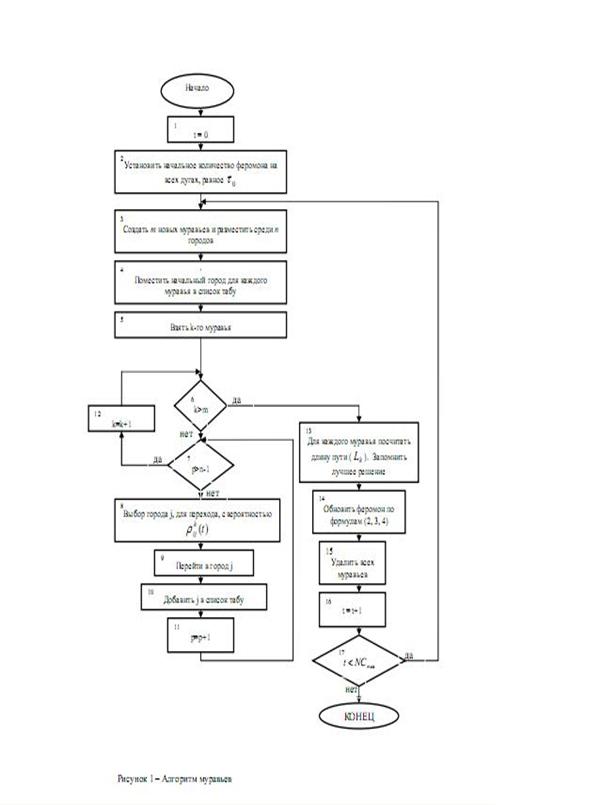
10. Демонстрационный пример
Разберем функционирование рассмотренного выше алгоритма на простом примере, чтобы увидеть, как работают уравнения. Возьмем простой сценарий с двумя муравьями из примера который рассмотрели в п. 1. На рис. 5 показан этот пример с двумя ребрами между двумя узлами (V0 и V1). Каждое ребро инициализируется и имеет одинаковые шансы на то, чтобы быть выбранным.
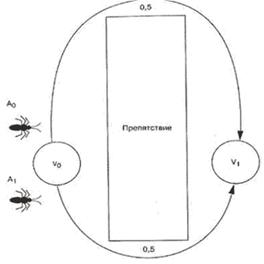
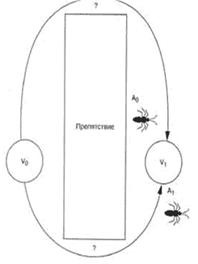
Рис. 5. Рис. 6.
Два муравья находятся в узле V0 помечаются как A0 и A1. Так как вероятность выбора любого пути одинакова, в этом цикле мы проигнорируем уравнение выбора пути. Данные для задачи:
число пройденных шагов: для A0 − 20, для A1 − 10
уровень феромона (Q/пройденное расстояние): для A0 − 0.5, A1 − 1.0
ρ = 0.5
α = 0.3
β = 1.0
На рис. 6 каждый муравей выбирает свой путь (муравей A0 идет по верхнему пути, а муравей A1 - по нижнему). Муравей A0 сделал 20 шагов, а муравей A1, - только 10. По уравнению 2 мы рассчитываем количество феромонов, которое должно быть "нанесено".
Примечание: Работу алгоритма можно изменить, переопределив его параметры (например, α, β или p), например, придав больший вес феромонам или расстоянию между узлами.
Далее по уравнению 3 рассчитывается количество феромона, которое будет применено. Для муравья A0 результат составляет: 0,1 + (0,5 * 0,6) = 0,4. Для муравья A1 результат составляет: 0,1 + (1,0 * 0,6) = 0,7. Далее с помощью уравнения 4 определяется, какая часть феромонов испарится и, соответственно, сколько останется. Результаты (для каждого пути соответственно) составляют:
0,4 * (1,0 - 0,6) = 0,16
0,7 * (0,5 - 0,6) = 0,28
Эти значения представляют новое количество феромонов для каждого пути (верхнего и нижнего, соответственно). Теперь переместим муравьев обратно в узел V0 воспользуемся вероятностным уравнением выбора пути 1, чтобы определить, какой путь должны выбрать муравьи. Вероятность того, что муравей выберет верхний путь (представленный количеством феромона 0,16), составляет:
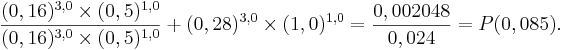
Вероятность того, что муравей выберет нижний путь (представленный количеством феромона 0,28) составляет:
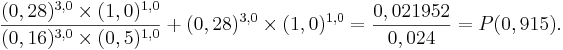
При сопоставлении двух вероятностей оба муравья выберут нижний путь, который является наиболее оптимальным.
11. Характерные особенности
Для алгоритма муравьиной колонии необходимо указать:
· закон выделения феромона,
· закон испарения феромона,
· количество агентов,
· места размещения.
Все эти характеристики выбираются с учетом особенности задачи на основе экспериментальных исследований (эвристики).
Алгоритм:
· реализует поиск приближенных решений,
· имеет полиномиальную сложность,
· является одним из видов вероятностных алгоритмов (законы выделения испарения – вероятностные законы).
12. Области применения
Алгоритм муравья может применяться для решения многих задач, таких как распределение ресурсов и работы.
При решении задачи распределения ресурсов необходимо задать группу ресурсов n для ряда адресатов m и при этом минимизировать расходы на перераспределение (то есть функция должна найти наилучший способ распределения ресурсов). Обнаружено, что алгоритм муравья дает решения такого же качества, как и другие, более стандартные способы.
Намного сложнее проблема распределения работы. В этой задаче группа машин М и заданий J (состоящих из последовательности действий, осуществляемых на машинах) должны быть распределены таким образом, чтобы все задания выполнялись за минимальное время. Хотя решения, найденные с помощью алгоритма муравья, не являются оптимальными, применение алгоритма для данной проблемы показывает, что с его помощью можно решать аналогичные задачи.
Алгоритм муравья применяется для решения других задач, например, прокладки маршрутов для автомобилей, расчета цветов для графиков и маршрутизации в сетях. Более подробно способы использования алгоритма муравья описываются в книге Марко Дориго «Алгоритмы муравья для абстрактной оптимизации»
Заключение
Рассмотрены механизмы реализации эвристических алгоритмов муравьиной колонии. Они могут быть успешно применены для решения сложных комбинаторных задач оптимизации. Основная идея, лежащая в основе алгоритмов муравьиной колонии, заключается в использовании механизма положительной обратной связи, который помогает найти наилучшее приближенное решение в сложных задачах оптимизации. То есть, если в данном узле муравей должен выбрать между различными вариантами и если фактически выбранные результаты будут хорошими, то в будущем такой выбор будет более желателен, чем предыдущий. Этот подход является многообещающим из-за его общности и эффективности в обнаружении очень хороших решений сложных проблем.
Список литературы
1. Джонс М.Т. Программирование искусственного интеллекта в приложениях / Пер. с англ. Осипов А.И. – Москва 2004
2. Журнал «Мир ПК». - №3. -2002
3. Сборник научных трудов СевКавГТУ. Серия «Естественнонаучная». 2006. №2
4. Штовба С.Д. Муравьиные алгоритмы. Exponenta Pro. Математика в приложениях, 2003, №4, стр. 70-75.
5. МакКоннелл Дж. Основы современных алгоритмов. – М.: Техносфера, 2004. – 368 с.
Похожие работы
... казалось принципиально невозможным. Очевидно, что эксперимент, опирающийся на традиционные способы поиска электромагнитных сигналов, не смог бы обнаружить этот канал. Почему же нельзя предположить, что распределенный мозг использует какой-то неизвестный нам способ передачи информации по каналу электромагнитных колебаний? С другой стороны, в повседневной жизни можно найти примеры передачи ...
... , 2004. – 382 с. 2. Инновационный менеджмент: Учеб. пособие / Под ред. В.М. Аньшина, А.А. Дагаева. – М.: Дело, 2003.- 528 с. Темы 12. Финансирование в инновационном менеджменте Лекция № 16 (к.т.н. Старовойтенко О.А.) План 12.1.Организационно - экономическое стимулирование нововведений. 12.2.Финансирование и кредитование нововведений. 12.3. Модели рынка нововведений и научно- ...
... системы развивающего обучения - свойства вариантности, учитывающего прежде всего индивидуальные особенности школьников. самоконтроль школьник тестовый орфографический Глава 3. Опытно-экспериментальная работа по формированию навыков орфографического самоконтроля у младших школьников на уроках русского языка Опытно-экспериментальная работа по проверке теоретически выделенных методов и ...
змы по-прежнему превосходили электронные, нам придётся поискать способ объединить компьютеры и человеческий мозг, либо попытаться искусственным путём усовершенствовать собственные гены. (Подробнее об этом рассказывается здесь) Впрочем, такие проекты пока остаются фантастикой. До их реализации пока ещё очень далеко, а пока главным предназначением устройств, подобных созданной в Мюнхене нейросхеме, ...






0 комментариев