Навигация
Прямая, содержащая хорду окружности, отличную от диаметра, является секущей равного наклона к осям, проходящим через концы хорды
3. Прямая, содержащая хорду окружности, отличную от диаметра, является секущей равного наклона к осям, проходящим через концы хорды.
4. Серединный перпендикуляр к любой хорде окружности является ее осью.
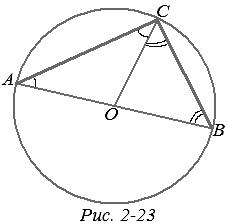
Не все свойства окружности, известные нам из школьного курса геометрии, имеют место на плоскости Лобачевского. Например, теорема о том, что угол, вписанный в окружность и опирающийся на диаметр, является прямым углом, неверна на плоскости Лобачевского. В самом деле, пусть угол АСВ, вписанный в окружность с центром О, опирается на диаметр АВ (рис. 2-23). Проведем радиус ОС и рассмотрим два равнобедренных треугольника ОАС и ОВС. Так как ![]() A =
A = ![]() АСО и
АСО и ![]() B =
B = ![]() BCO, то
BCO, то ![]() A +
A + ![]() В =
В = ![]() АСО +
АСО + ![]() ВСО =
ВСО =![]() АСВ. Следовательно, σABC =
АСВ. Следовательно, σABC = ![]() A +
A + ![]() В +
В + ![]() АВС = 2
АВС = 2![]() АСВ. Значит,
АСВ. Значит, ![]() АСВ =
АСВ = ![]() σABC . Так как σABC < 2d, то АСВ < d, т. е.
σABC . Так как σABC < 2d, то АСВ < d, т. е. ![]() АСВ — острый угол.
АСВ — острый угол.
Эквидистанта. Эквидистантой называется фигура, которая состоит из всех точек полуплоскости с границей и, равноудаленных от этой прямой. Прямая и называется базой эквидистанты, а перпендикуляр, проведенный из любой точки эквидистанты на базу,— высотой. Высотой называется также длина h этого перпендикуляра.
С эквидистантой связан пучок расходящихся прямых — множество всех прямых, перпендикулярных к базе эквидистанты. Прямые этого пучка называются осями эквидистанты. Многие свойства эквидистанты аналогичны свойствам окружности.
Убедимся в том, что эквидистанта — кривая линия.
Теорема 1. Любая прямая, лежащая в плоскости эквидистанты, пересекается с эквидистантой не более, чем в двух точках.
доказательство
Рассмотрим другие свойства эквидистанты.
1. Эквидистанта симметрична относительно любой своей оси.
доказательство
2. В каждой точке эквидистанты существует касательная, которая перпендикулярна к оси, проведенной через точку касания.
доказательство
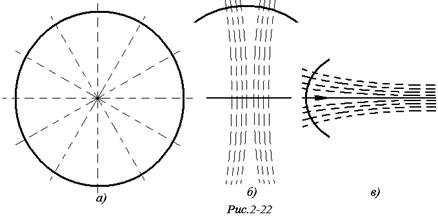
Учитывая это свойство, мы можем говорить, что эквидистанта является ортогональной траекторией пучка расходящихся прямых, перпендикулярных к базе эквидистанты (см. рис. 2-22, б).
Хордой эквидистанты назовем любой отрезок, соединяющий две точки эквидистанты.
3°. Любая прямая, содержащая хорду эквидистанты, является секущей равного наклона к осям, проходящим через концы хорды.
доказательство
4°. Серединный перпендикуляр к любой хорде эквидистанты является ее осью.
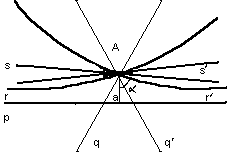
Орицикл. Прежде чем ввести понятие орицикла, докажем следующую лемму.
Лемма. Через каждую точку одной из двух параллельных прямых проходит одна и только одна секущая равного наклона к этим прямым.
доказательство
Пусть на плоскости задан пучок параллельных прямых. На множестве Ω всех точек плоскости введем бинарное отношение ∆ следующим образом. Будем говорить, что точки A и В находятся в отношении ∆, если они совпадают или прямая АВ является секущей равного наклона к прямым данного пучка, проходящим соответственно через точки А и В. Из этого определения непосредственно следует, что отношение ∆ удовлетворяет условиям рефлексивности и симметричности. Можно также доказать, что оно удовлетворяет условию транзитивности. Каждый элемент фактор-множества Ω/∆ называется орициклом (или предельной линией). Прямые данного пучка называются осями орицикла. Если задан пучок параллельных прямых, то через каждую точку А плоскости проходит один и только один орицикл, который представляет собой класс эквивалентности КА по отношению ∆. Это множество состоит из точки А и всех таких точек X плоскости, что АХ -секущая равного наклона к прямым данного пучка, проходящим через точки А и X.
Если даны направленная прямая UV и на ней некоторая точка А, то тем самым однозначно определяется орицикл, проходящий через точку А с осью UV.
Свойства орицикла аналогичны свойствам окружности и эквидистанты.
Теорема 2. Любая прямая, лежащая в плоскости орицикла, пересекается с орициклом не более чем в двух точках.
доказательство
Орицикл симметричен относительно любой своей оси и является ортогональной траекторией пучка его параллельных осей (см. рис 2-22, в).
Любые два орицикла на плоскости Лобачевского равны.
Гиперболическое пространство
Пусть V — векторное пространство размерности п над полем R (в дальнейшем будем рассматривать значения п = 2,3). Зададим билинейную форму g: V ![]() V → R, такую, чтобы квадратичная форма φ (
V → R, такую, чтобы квадратичная форма φ (![]() ) = g (
) = g (![]() ,
,![]() ) была бы невырожденной квадратичной формой индекса k > 0. Число g (
) была бы невырожденной квадратичной формой индекса k > 0. Число g (![]() ,
,![]() )
)![]() R назовем скалярным произведением векторов
R назовем скалярным произведением векторов ![]() ,
, ![]() и обозначим через
и обозначим через ![]() ·
·![]() или
или ![]()
![]() , а число
, а число 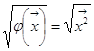 длиной (нормой) вектора
длиной (нормой) вектора ![]() . Таким образом, если
. Таким образом, если ![]() , то
, то ![]() , а если
, а если ![]() , то
, то ![]() , где b > 0 и i2 = -1.
, где b > 0 и i2 = -1.
Векторное пространство V, в котором скалярное произведение определено при помощи указанной выше билинейной формы g, называется псевдоевклидовым векторным пространством индекса k.
В псевдоевклидовом пространстве скалярный квадрат ![]() вектора
вектора ![]() ≠ 0 может быть положительным, отрицательным или нулем. Например, если в базисе В = (
≠ 0 может быть положительным, отрицательным или нулем. Например, если в базисе В = (![]() ) квадратичная форма φ (
) квадратичная форма φ (![]() ) имеет нормальный вид:
) имеет нормальный вид:
φ(![]() ) = (x1)2+ …+ (xn-k)2 – (xn-k+1)2 – … – (xn)2 , (1)
) = (x1)2+ …+ (xn-k)2 – (xn-k+1)2 – … – (xn)2 , (1)
то, очевидно, для векторов базиса имеем:
![]() ,
, ![]() ,…,
,…, ![]() ,
,![]() , …,
, …,![]() .
.
Поэтому длина каждого из векторов ![]() равна единице; это единичные векторы. Каждый из векторов
равна единице; это единичные векторы. Каждый из векторов ![]() имеет мнимую длину i; назовем эти векторы мнимоединичными.
имеет мнимую длину i; назовем эти векторы мнимоединичными.
Вектор ![]() ≠
≠ ![]() , для которого
, для которого ![]() = 0, называется изотропным. Длины этих векторов равны нулю. Каждый из векторов
= 0, называется изотропным. Длины этих векторов равны нулю. Каждый из векторов ![]() , где
, где ![]() и
и ![]() — векторы базиса В при р
— векторы базиса В при р ![]() п — k, q > n — k, является изотропным, так как по формуле (1)
п — k, q > n — k, является изотропным, так как по формуле (1)
φ(![]() ) = 1 – 1=0.
) = 1 – 1=0.
По-прежнему два вектора ![]() ,
, ![]() будем называть ортогональными, если
будем называть ортогональными, если ![]()
![]() = 0. Векторы базиса В, в котором квадратичная форма имеет нормальный вид (1), попарно ортогональны, так как эти векторы попарно сопряжены относительно билинейной формы g(
= 0. Векторы базиса В, в котором квадратичная форма имеет нормальный вид (1), попарно ортогональны, так как эти векторы попарно сопряжены относительно билинейной формы g(![]() ,
,![]() ).
).
Таким образом, базис В состоит из единичных и мнимоединичных попарно ортогональных векторов. Такой базис назовем ортонормированным. Так как индекс квадратичной формы φ (![]() ) не зависит от способа приведения этой формы к нормальному виду, то все ортонормированные базисы псевдоевклидова векторного пространства V содержат одинаковое число мнимоединичных векторов; это число равно индексу пространства.
) не зависит от способа приведения этой формы к нормальному виду, то все ортонормированные базисы псевдоевклидова векторного пространства V содержат одинаковое число мнимоединичных векторов; это число равно индексу пространства.
Пусть В — ортонормированный базис, а векторы ![]() и
и ![]() в этом базисе имеют координаты (xi) и (уi). Тогда
в этом базисе имеют координаты (xi) и (уi). Тогда ![]() = хi
= хi![]() и у = yi
и у = yi![]() , поэтому
, поэтому
![]()
![]() =x1y1 + x2y2 + …+ xn-kyn-k – xn-k+1yn-k+1 - …- xnyn . (2)
=x1y1 + x2y2 + …+ xn-kyn-k – xn-k+1yn-k+1 - …- xnyn . (2)
Докажем следующую теорему.
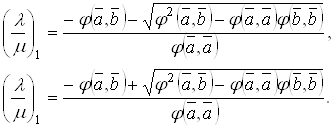
Теорема. В псевдоевклидовом векторном пространстве V индекса 1 для любых двух векторов мнимой длины справедливо неравенство
(![]()
![]() )2
)2![]()
![]()
![]()
причем знак равенства в этой формуле имеет место тогда и только тогда, когда векторы ![]() и
и ![]() коллинеарны.
коллинеарны.
доказательство
Следствие. В псевдоевклидовом векторном пространстве индекса 1 для любых двух векторов ![]() ,
, ![]() мнимой длины справедливо неравенство
мнимой длины справедливо неравенство
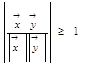 (3)
(3)
Пусть V — псевдоевклидово векторное пространство индекса размерности п + 1 над полем R (n = 2,3) и g (![]() ,
,![]() ) — билинейная форма, с помощью которой в пространстве V определено скалярное произведение. Мы будем рассматривать только автоморфизмы пространства V, т. е. такие линейные преобразования этого пространства, которые сохраняют скалярное произведение векторов (и значит, сохраняют длины векторов). Обозначим через Ω* множество всех векторов мнимой длины пространства V. Очевидно, что если φ — автоморфизм пространства V, то φ (Ω*) = Ω*.
) — билинейная форма, с помощью которой в пространстве V определено скалярное произведение. Мы будем рассматривать только автоморфизмы пространства V, т. е. такие линейные преобразования этого пространства, которые сохраняют скалярное произведение векторов (и значит, сохраняют длины векторов). Обозначим через Ω* множество всех векторов мнимой длины пространства V. Очевидно, что если φ — автоморфизм пространства V, то φ (Ω*) = Ω*.
Множество Е ≠ 0 называется п-мерным гиперболическим пространством Лобачевского (и обозначается через ![]() ), если задано отображение
), если задано отображение
π : Ω*→E,
удовлетворяющее следующим аксиомам:
1) π— сюръекция;
2) π(![]() ) = π(
) = π(![]() ) тогда и только тогда, когда
) тогда и только тогда, когда ![]() и
и ![]() коллинеарны.
коллинеарны.
Систему аксиом 1—2 пространства Лобачевского обозначим через ![]() .
.
Элементы множества Е называются точками. Так же как и в случае проективного пространства, если X = π (![]() ), то будем говорить, что точка X порождена вектором
), то будем говорить, что точка X порождена вектором ![]() .
.
Расстояние между точками X, Y ![]()
![]() , определяется следующим образом. Зададим положительное число r (одно и то же для данного пространства
, определяется следующим образом. Зададим положительное число r (одно и то же для данного пространства ![]() ). Если точки X, Y порождаются векторами
). Если точки X, Y порождаются векторами ![]() ,
, ![]()
![]() Ω*, то назовем расстоянием между этими точками неотрицательное число δ(X, Y), удовлетворяющее равенству
Ω*, то назовем расстоянием между этими точками неотрицательное число δ(X, Y), удовлетворяющее равенству
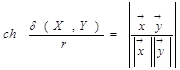 (4)
(4)
где ch t = ![]() - гиперболический косинус вещественной переменной t. Мы замечаем, что функция cht четная, определена на всей числовой оси и ее значения заполняют промежуток [1, + ∞]. Поэтому согласно формуле (3) расстояние между любыми двумя точками всегда существует и является положительным числом.
- гиперболический косинус вещественной переменной t. Мы замечаем, что функция cht четная, определена на всей числовой оси и ее значения заполняют промежуток [1, + ∞]. Поэтому согласно формуле (3) расстояние между любыми двумя точками всегда существует и является положительным числом.
Число r > 0 называется радиусом кривизны пространства ![]() .
.
Правая часть формулы (4) показывает, что расстояние δ(X, Y) не зависит от выбора векторов, порождающих точки X и Y.
Всякий автоморфизм φ псевдоевклидова векторного пространства индуцирует некоторое преобразование f пространства ![]() по закону:
по закону:
если
φ (![]() ) =
) = ![]() , то f(X) = X’.
, то f(X) = X’.
Из формулы (4) следует, что преобразование f сохраняет расстояние между любыми двумя точками пространства ![]() . Такое преобразование f называется движением пространства
. Такое преобразование f называется движением пространства ![]() .
.
Из определения пространства ![]() можно заключить, что гиперболические пространства Лобачевского
можно заключить, что гиперболические пространства Лобачевского ![]() и
и ![]() ' одной и той же размерности изоморфны. Следовательно, система аксиом
' одной и той же размерности изоморфны. Следовательно, система аксиом ![]() категорична, теория T (
категорична, теория T (![]() ) однозначна и ее можно изучать, пользуясь любой интерпретацией.
) однозначна и ее можно изучать, пользуясь любой интерпретацией.
Докажем, что система аксиом ![]() непротиворечива, если непротиворечива арифметика вещественных чисел. Для этого построим интерпретацию этой системы, используя множество R вещественных чисел. Для простоты изложения ограничимся случаем, когда п = 2, т. е. когда Е — плоскость Лобачевского.
непротиворечива, если непротиворечива арифметика вещественных чисел. Для этого построим интерпретацию этой системы, используя множество R вещественных чисел. Для простоты изложения ограничимся случаем, когда п = 2, т. е. когда Е — плоскость Лобачевского.
Вектором псевдоевклидова векторного пространства V индекса 1 размерности 3 назовем любой столбец вида ![]() , где а1, a2, a3 — произвольные вещественные числа. Сумма векторов и умножение вектора на число вводятся обычным образом, т. е. как сумма столбцов и умножение столбца на число.
, где а1, a2, a3 — произвольные вещественные числа. Сумма векторов и умножение вектора на число вводятся обычным образом, т. е. как сумма столбцов и умножение столбца на число.
Скалярным произведением векторов ![]() и
и ![]() назовем число a1b1 + а2b2 - а3b3. Мы получили модель псевдоевклидова векторного пространства индекса 1 размерности 3. Очевидно, множество Ω* всех векторов мнимой длины состоит из тех и только тех векторов
назовем число a1b1 + а2b2 - а3b3. Мы получили модель псевдоевклидова векторного пространства индекса 1 размерности 3. Очевидно, множество Ω* всех векторов мнимой длины состоит из тех и только тех векторов ![]() , для которых
, для которых ![]() .
.
Введем следующее обозначение. Множество всех троек чисел вида km1, km2, km3, где k — любое действительное число, отличное от нуля, а m1, т2, m3 - фиксированные числа, не равные одновременно нулю, обозначим через < m1, т2, m3>. ■
Точкой (т. е. элементом множества Е) назовем любое множество < m1, т2, m3> при условии, что ![]() . Отображение π : Ω*→E определим так: вектору
. Отображение π : Ω*→E определим так: вектору ![]() поставим в соответствие точку < m1, т2, m3> , такую, что (а1, а2, а3)
поставим в соответствие точку < m1, т2, m3> , такую, что (а1, а2, а3) ![]() < m1, т2, m3 >
< m1, т2, m3 >
В построенной интерпретации, очевидно, выполняются обе аксиомы системы ![]() .
.
Рассмотренное выше утверждение позволяет дать еще один способ доказательства независимости аксиомы параллельных от остальных аксиом евклидовой геометрии .
Система аксиом ![]() Гильберта евклидовой геометрии состоит из аксиом I, II, III, IV, V групп, где V — аксиома параллельных, эквивалентная (при сохранении аксиом I — IV) V постулату Евклида. Выше было доказано, что система аксиом
Гильберта евклидовой геометрии состоит из аксиом I, II, III, IV, V групп, где V — аксиома параллельных, эквивалентная (при сохранении аксиом I — IV) V постулату Евклида. Выше было доказано, что система аксиом ![]() непротиворечива, если непротиворечива арифметика вещественных чисел. В последующем мы ограничимся геометрией на плоскости, поэтому все системы аксиом будем рассматривать лишь для плоскости.
непротиворечива, если непротиворечива арифметика вещественных чисел. В последующем мы ограничимся геометрией на плоскости, поэтому все системы аксиом будем рассматривать лишь для плоскости.
Рассмотрим систему аксиом ∑* = (![]() \V) U V*. где V* — аксиома Лобачевского. Обозначим через
\V) U V*. где V* — аксиома Лобачевского. Обозначим через ![]() систему аксиом 1—2 плоскости Лобачевского
систему аксиом 1—2 плоскости Лобачевского ![]() . Выше мы доказали, что эта система непротиворечива. При этом система аксиом
. Выше мы доказали, что эта система непротиворечива. При этом система аксиом ![]() категорична (все ее интерпретации изоморфны). Можно доказать (с помощью достаточно длинных рассуждений), что системы аксиом ∑* и
категорична (все ее интерпретации изоморфны). Можно доказать (с помощью достаточно длинных рассуждений), что системы аксиом ∑* и ![]() эквивалентны.
эквивалентны.
Следовательно, для системы ∑* нашлась интерпретация — это та же интерпретация, что и интерпретация системы ![]() . Поэтому система аксиом ∑* (содержательно) непротиворечива. Но в таком случае из самого способа составления этой системы аксиом следует, что аксиома параллельных V не зависит от остальных аксиом (
. Поэтому система аксиом ∑* (содержательно) непротиворечива. Но в таком случае из самого способа составления этой системы аксиом следует, что аксиома параллельных V не зависит от остальных аксиом (![]() \ V) евклидовой геометрии.
\ V) евклидовой геометрии.
Замечание. Так как аксиома параллельных V эквивалентна V постулату Евклида, то полученный результат можно еще сформулировать так: V постулат Евклида не зависит от остальных аксиом системы ![]() .
.
Модель Кэли — Клейна плоскости Лобачевского
Эта модель называется также моделью Кэли — Клейна. Ее построил английский математик Кэли, но он не понял, что введенная им геометрия в круге и есть геометрия Лобачевского; это сообразил позже, в 1870 г., немецкий математик Клейн.
1. Плоскость Лобачевского Λ2 порождена множеством Q* векторов мнимой длины трехмерного псевдоевклидова пространства V (индекса 1). Скалярное произведение векторов пространства V определяется при помощи заданной билинейной формы g(х, у), такой, что g(x, х) — невырожденная квадратичная форма индекса 1.
Рассмотрим проективную модель плоскости Λ2. На проективной плоскости Р2, порожденной векторным пространством V, квадратичная форма g(х, х) определяет линию второго порядка Q : Ф (X) = 0, где Ф (X) = g(х, х), и вектор ![]() порождает точку XÎP2. При этом на плоскости Р2 рассматриваются не любые проективные преобразования, а только те, которые порождены автоморфизмами псевдоевклидова векторного пространства V. Такие проективные преобразования образуют стационарную подгруппу НQ кривой второго порядка Q.
порождает точку XÎP2. При этом на плоскости Р2 рассматриваются не любые проективные преобразования, а только те, которые порождены автоморфизмами псевдоевклидова векторного пространства V. Такие проективные преобразования образуют стационарную подгруппу НQ кривой второго порядка Q.
Пусть ![]() — ортонормированный базис пространства V, причем
— ортонормированный базис пространства V, причем ![]() — мнимоединичный вектор. Если в этом базисе вектор
— мнимоединичный вектор. Если в этом базисе вектор ![]() имеет координаты
имеет координаты![]()
![]() , то, очевидно
, то, очевидно ![]() . Базис В порождает проективный репер R = (А1, А2, A3, E) плоскости Р2. В этом репере в силу предыдущего равенства линия Q определяется уравнением
. Базис В порождает проективный репер R = (А1, А2, A3, E) плоскости Р2. В этом репере в силу предыдущего равенства линия Q определяется уравнением
![]() .
.
Следовательно, Q — овальная линия второго порядка.
Напомним, что точка![]() является внутренней точкой относительно линии Q тогда и только тогда, когда
является внутренней точкой относительно линии Q тогда и только тогда, когда ![]() . Это означает, что точка М порождена вектором
. Это означает, что точка М порождена вектором ![]() мнимой длины, т. е.
мнимой длины, т. е. ![]() .
.
Таким образом, при отображении определяющем проективную плоскость Р2, множество p(W*)=Λ2 есть множество точек, внутренних относительно овальной линии Q.
Так как при отображении p аксиомы ΣΛ выполняются, то множество p(W*)=Λ2 точек, внутренних относительно кривой Q, является моделью плоскости Лобачевского. Линия второго порядка Q называется абсолютом плоскости Лобачевского Λ2.
Похожие работы
... 3. Б.Л. Лаптев. Н.И. Лобачевский и его геометрия. Пособие для учащихся. М. «Просвещение», 1970г. 4. И.М. Яглам. Принцип относительности Галилея и неевклидова геометрия.Серия «Библиотека математического кружка» М: 1963г. Приложение 1 Николай Иванович Лобачевский, второй сын мелкого чиновника, родился 1 декабря(20 ...
... , т. е. такие пары точек считаются за одну точку. Из этого определения следует, что при возрастании n число типов неевклидовых пространств также растет. Неевклидовы геометрии являются геометриями простейших римановых пространств определенной и неопределенной метрики, составляющих так называемый класс пространств постоянной ненулевой кривизны. Каждое из таких n-мерных пространств допускает ...
... метод координат. V. Аксіома паралельності Сама остання аксіома грає в геометрії особливу роль, визначаючи поділ геометрії на дві логічно несуперечливі й взаємно виключають один одного системи: Евклідову й неевклідову геометрії. У геометрії Евкліда ця аксіома формулюється так. V. Нехай а – довільна пряма й А – крапка, що лежить поза прямій а, тоді в площині α, обумовленою крапкою А и ...
... представить другие геометрии Кант счел достаточным основанием, чтобы утверждать, что другие геометрии не могут существовать. Появление неевклидовой геометрии Но многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой, а в ...

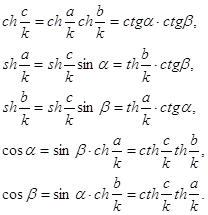
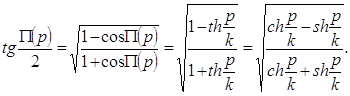
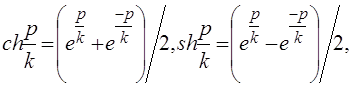
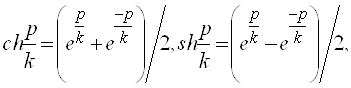
0 комментариев