Навигация
Докажем теорему о перпендикулярных прямых на модели Кэли — Клейна
3. Докажем теорему о перпендикулярных прямых на модели Кэли — Клейна.
Теорема 3. Прямые АВ и CD на плоскости А2 перпендикулярны тогда и только тогда, когда они изображаются хордами абсолюта Q, лежащими на проективных прямых, каждая из которых проходит через полюс другой.
доказательство
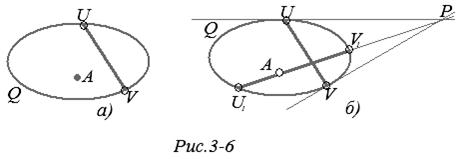
Замечание. Используя доказанную теорему, легко решить следующую задачу на модели Кэли — Клейна. На плоскости Λ2 даны прямая UV и точка А, не лежащая на ней (рис.3-6, а). Построить прямую, проходящую через точку А и перпендикулярную к прямой UV. На плоскости Р2 строим полюс Р проективной прямой UV и проводим проективную прямую АР, которая пересекает абсолют Q в точках U1, V1 (рис. 3-6, б). По доказанной теореме хорда U1, V1 является искомой прямой плоскости Λ2.
4. Мы отметили, что в интерпретации Кэли — Клейна две расходящиеся прямые изображаются такими хордами абсолюта, что проективные прямые, содержащие эти хорды, пересекаются во внешней точке относительно абсолюта. Выше было доказано, что если две прямые имеют общий перпендикуляр, то они расходятся (§3 Гл.1, теорема 3). Докажем обратную теорему.
Теорема 4. Две расходящиеся прямые UV и U'V' имеют общий перпендикуляр, и притом единственный.
Теорема 4. Две расходящиеся прямые UV и U'V' имеют общий перпендикуляр, и притом единственный.
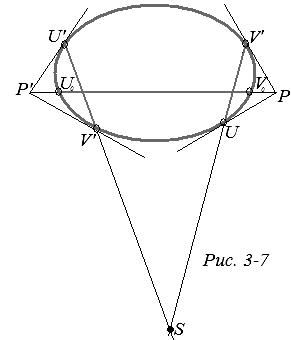
Пусть Р и Р' — полюсы проективных прямых UV и U'V’ соответственно, a S — точка пересечения проективных прямых UV и U'V’ на проективной плоскости Р2 (рис. 3-7). Прямая РР' проходит через полюсы прямых UV и U'V’, поэтому по теореме взаимности поляритета проективные прямые UV и U'V’ проходят через полюс прямой РР'. Но UV∩U'V’=S, следовательно, S — полюс прямой РР'. По условию S — внешняя точка относительно абсолюта, и, значит, ее поляра — прямая РР' пересекает абсолют в двух точках U0 и V0.
Так как проективная прямая U0V0 проходит через полюсы Р и Р' прямых UV и U'V (рис.3-7), то по теореме 3 U0V0^UV и U0V0^U’V’, т. е. прямая U0V0 на плоскости Λ2 является общим перпендикуляром двух расходящихся прямых UV и U'V’. Такая прямая единственная, так как по этой же теореме искомая хорда абсолюта должна лежать на проективной прямой, проходящей через точки Р и Р', а через две точки проективной плоскости проходит только одна прямая.
Понятие о сферической геометрии
1. Сферическая геометрия изучает свойства фигур, лежащих на сфере евклидова пространства.
Пусть S — некоторая сфера с центром О радиуса r. Возьмем плоскость s, удаленную от точки О на расстояние, меньшее r. Тогда пересечение плоскости s и сферы S есть окружность, которую назовем большой окружностью, если ОÎs, и малой окружностью, если ОÎs.
В геометрии на сфере большие окружности играют роль прямых на плоскости. Здесь есть определенная аналогия: для любых двух точек А, ВÎS существует большая окружность, проходящая через эти точки. Но есть и отличие: большая окружность единственная только тогда, когда точки А и В не являются диаметрально противоположными. Далее, на плоскости Евклида и на плоскости Лобачевского существуют непересекающиеся прямые, тогда как на сфере любые две различные большие окружности пересекаются в двух точках (диаметрально противоположных).
Известно, что любая большая окружность Q сферы S делит ее на две части, которые называются полусферами, а сама окружность Q — краем этих полусфер. В геометрии на сфере полусфера играет ту же роль, что и полуплоскость в планиметрии.
Пусть А и В — две диаметрально противоположные точки сферы S, АСВ и ADB — две какие-либо полуокружности с концами в точках А и В, а фигура Г — объединение этих полуокружностей (рис.3-8).
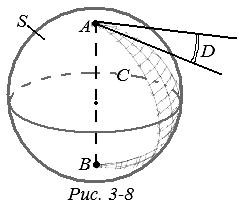
Можно показать, что фигура Г делит фигуру S\Г на две части D' и D" (на рис. 3-8 одна из этих частей заштрихована). Каждая из фигур D1=D’ÈГ, D2=D"ÈГ называется двуугольником с вершинами в точках А и В.
Данные полуокружности АСВ и ADB называются сторонами этих двуугольников. Двуугольник — аналог угла на плоскости: двуугольник является или пересечением, или объединением двух полусфер, края которых не совпадают. Ясно, что двуугольник можно рассматривать как пересечение сферы S с двугранным углом С× АВ× D. Линейный угол этого двугранного угла называется углом данного двуугольника. Его можно рассматривать как угол между касательными в точке А (или В) к большим окружностям, содержащим стороны двуугольника. Если этот угол прямой, то двуугольник называется прямоугольным.
Пусть Q1 и Q2 — две большие окружности. Q1∩Q2 ={А,В}. Мы имеем здесь две пары вертикальных двуугольников, высекаемых на сфере S двумя парами вертикальных двугранных углов, полученных при пересечении плоскостей s1ÉQ1 и s2ÉQ2. Если один из этих двуугольников прямоугольный, то и остальные три прямоугольные. В этом случае большие окружности Q1 и Q2 называются перпендикулярными: Q1^Q2. Ясно, что окружности Q1 и Q2 перпендикулярны тогда и только тогда, когда плоскости s1 и s2 перпендикулярны.
Если Q — большая окружность, а АВ — диаметр сферы, перпендикулярный к плоскости этой окружности, то точки А и В называются полюсами окружности Q. Если точка M1 не является полюсом окружности Q, то существует, и притом единственная, большая окружность Q2, проходящая через точку M1 и перпендикулярная окружности Q. Чтобы получить эту окружность Q2, надо пересечь сферу S плоскостью, которая проходит через прямую ОМ1 перпендикулярно плоскости окружности Q1. Если же точка M1 является полюсом большой окружности Q1, то любая большая окружность, проходящая через точку M1, перпендикулярна окружности Q1. В этом снова проявляется отличие сферической геометрии от геометрии на евклидовой плоскости (или на плоскости Лобачевского), где через любую точку плоскости проходит единственная прямая, перпендикулярная к данной прямой.
2. Возьмем две точки A,BÎS и рассмотрим большую окружность Q, проходящую через эти точки (рис. 3-9). Окружность Q является объединением двух своих дуг ![]() и
и ![]() с концами в точках А и В. Длина той из этих двух дуг, которая не больше полуокружности, называется сферическим расстоянием между точками А и В и обозначается через d(A,B). Следовательно, для любых двух точек сферы S имеем d(A,B)£pr.
с концами в точках А и В. Длина той из этих двух дуг, которая не больше полуокружности, называется сферическим расстоянием между точками А и В и обозначается через d(A,B). Следовательно, для любых двух точек сферы S имеем d(A,B)£pr.
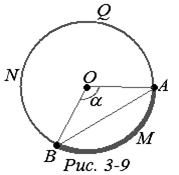
Пусть ![]() меньше полуокружности, и, значит, d(A,B) — длина этой дуги. Обозначим через а величину центрального угла АОВ, опирающегося на дугу АМВ, и через r(А,В) – длину отрезка АВ. Как известно,
меньше полуокружности, и, значит, d(A,B) — длина этой дуги. Обозначим через а величину центрального угла АОВ, опирающегося на дугу АМВ, и через r(А,В) – длину отрезка АВ. Как известно,
d(A,B) = ar. (1)
Из треугольника АОВ (рис. 3-9) находим:
![]() (2)
(2)
Из формул (1), (2) следует:
![]() (3)
(3)
3. Движением сферы называется всякое изометрическое отображение этой сферы на себя, т. е. такое отображение f: S®S, которое удовлетворяет условию: каковы бы ни были точки А и В сферы, d(A,B) = d(f(A), f(B)). Из формулы (3) следует, что в этом случае r(А,В)=r(f(А), f(В)). Следовательно, любое движение f сферы S порождается некоторым движением f0 пространства, причем f0(О)=О. Обратно: любое движение g0 пространства, оставляющее точку О инвариантной, порождает определенное движение сферы S.
Отсюда заключаем, что множество всех движений сферы S является группой, которая изоморфна стационарной подгруппе Н0 точки О в группе движений пространства.
Две фигуры F, F'Ì S называются конгруэнтными или равными, если существует такое движение сферы S, которое переводит одну из этих фигур в другую. Следовательно, фигуры F, F' Ì S конгруэнтны, если они Н0 – эквивалентны.
4. Возьмем на сфере S три точки А,В,С, не лежащие на одной большой окружности. Они определяют три полусферы, каждая из которых содержит точки А,В,С, причем две из этих точек принадлежат краю полусферы. Пересечение этих трех полусфер называется сферическим треугольником с вершинами А,В,С. Дуги АВ, ВС, АС больших окружностей (меньшие полуокружности) называются сторонами сферического треугольника ABC.
Пусть ABC — сферический треугольник, а = d(B,C), b = d(A,C), с = d(A,B) — длины его сторон, a, b, g соответственно углы ВОС, АОС и АОВ.
Докажем теорему синусов для сферического треугольника.
Теорема. Пусть а=d{B,C), b=d{A,C), с=d{A,B) — стороны сферического треугольника ABC, a r — радиус сферы. Тогда
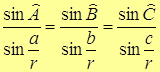 (4)
(4)
доказательство
Можно доказать, что справедливо следующее равенство, которое выражает теорему косинусов для сферического треугольника ABC:
![]() (7).
(7).
Можно так же доказать, что площадь сферического треугольника ABC вычисляется по формуле
![]() , (8)
, (8)
где ![]() — так называемый избыток сферического треугольника. Так как площадь SABC>0, то из формулы (8) следует,что e> 0, т. е.
— так называемый избыток сферического треугольника. Так как площадь SABC>0, то из формулы (8) следует,что e> 0, т. е. ![]() . Итак, сумма углов любого сферического треугольника больше p. Это — существенное отличие геометрии на сфере как от геометрии на плоскости Евклида, так и от геометрии на плоскости Лобачевского
. Итак, сумма углов любого сферического треугольника больше p. Это — существенное отличие геометрии на сфере как от геометрии на плоскости Евклида, так и от геометрии на плоскости Лобачевского
Модель Пуанкаре
Модель Пуанкаре геометрии Лобачевского. (Французский ученый Анри Пуанкаре (1854—1912) — крупнейший математик. Описываемая далее модель была предложена им в 1882г.) Роль плоскости Лобачевского играет открытая полуплоскость; роль прямых выполняют содержащиеся в ней полуокружности с центрами на ограничивающей ее прямой и лучи, перпендикулярные этой прямой. Роль наложений выполняют композиции инверсий относительно этих полуокружностей и отражений в лучах. Все аксиомы евклидовой геометрии здесь выполняются, кроме аксиомы параллельных (рис. 4-1, а), тем самым в этой модели выполняется геометрия Лобачевского.

Опишем эту модель более подробно и докажем сказанное. Берем на обычной евклидовой плоскости какую-нибудь прямую р и ограниченную ею открытую полуплоскость Р. Прямую р назовем граничной прямой. Полуплоскость Р будет играть роль плоскости Лобачевского; мы будем называть ее «плоскостью» в кавычках. Точками в модели будут точки этой «плоскости», т. е. полуплоскости Р. За «прямые» в модели принимаем, во-первых, содержащиеся в Р полуокружности, центры которых лежат на граничной прямой (рис. 4-1, а). «Отрезок» АВ в модели — это дуга такой полуокружности с концами A, В.
Подчеркнем, что конец «отрезка» не может быть концом полуокружности, представляющей прямую; ее концы исключены вместе с граничной прямой; «плоскость» — это открытая полуплоскость. Точка «прямой» служит общим началом двух «лучей» — двух дуг полуокружности (с исключенными концами). «Углом» назовем фигуру из двух «лучей» с общим началом, не содержащихся в одной «прямой» (рис. 4-1, а).
Помимо указанных «прямых» есть еще «прямые» — это полупрямые, перпендикулярные граничной прямой. Они являются пределами рассмотренных полуокружностей (рис. 4-1,б). Когда центр полуокружности удаляется по граничной прямой, а полуокружность проходит через данную точку, то она «распрямляется» и в пределе переходит в полупрямую. Поэтому мы дальше будем мыслить указанные полупрямые среди «прямых» модели в качестве полуокружностей, как «полуокружности бесконечного радиуса». Это позволит обойтись без скучных оговорок, касающихся этих полупрямых, причем, однако, следует помнить условность этого и быть готовым проверять утверждения для таких «полуокружностей». («Отрезок» на такой «прямой» — это обычный отрезок, а «лучи» — один обычный луч, другой — отрезок с исключенным концом на граничной прямой.)
Рассмотрим теперь в этой модели те аксиомы, в которые не входит понятие о равенстве отрезков и углов.
Аксиома параллельных для прямых относится к таким аксиомам. В данной модели она явно не выполняется: через точку А, не лежащую на «прямой» а, проходит бесконечно много «прямых», не имеющих с а общих точек (рис. 4-1,а).
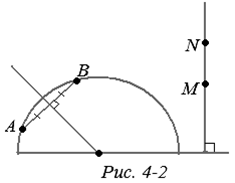
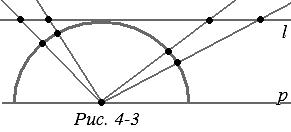
Все прочие аксиомы, говорящие о связи точек и отрезков или точек и прямых, о взаимном расположении точек и прямых, здесь выполняются. Так, на рис. 4-2 указано построение отрезка с данными концами. Далее, возьмем полуокружность, представляющую «прямую» в модели. Проведем прямую l, касающуюся этой полуокружности и параллельную граничной прямой. Спроектируем полуокружность из ее центра на прямую l (рис.4-3). Получим взаимно однозначное, сохраняющее порядок точек, соответствие между точками прямой и полуокружности, т. е. «прямой» модели. Все свойства, выраженные в аксиомах, будут одни и те же. Они также очевидно выполнены на полупрямых, представляющих «прямые» модели. Аксиома деления плоскости также выполняется. «Прямая» — полуокружность — делит плоскость на две области — внутреннюю и внешнюю. Это и будут «полуплоскости» в нашей модели. Из одной в другую нельзя перейти по какой-либо дуге, не пересекая разделяющую их «прямую» — полуокружность.
Остается определить равенство «отрезков» и «углов» так, чтобы выполнялись соответствующие аксиомы. Это мы сделаем, определив «наложение». Сначала определим «отражение в прямой». За «отражение в прямой» примем инверсию в той окружности, полуокружность которой представляет данная «прямая». Если же «прямая» — это полупрямая, перпендикулярная граничной прямой, то «отражением» в ней будет обычное отражение.
«Наложением» в модели называем любую композицию «отражений». «Равными» считаем фигуры, в частности, «отрезки» и «углы», совмещаемые «наложением».
Это определение сразу приводит к выводу: углы, «равные» в модели, равны без кавычек — в обычном смысле. В самом деле, углы при инверсиях сохраняются, т. е. преобразуются в равные, но они «равны» в модели по определению. Обратно: углы, «равные» в модели, — это т.е., которые преобразуются друг в друга «наложениями», т. е. инверсиями, и, стало быть, они равны в обычном смысле.
При инверсии в окружности с центром на граничной прямой эта прямая и полуплоскость Р отображаются на себя. Поэтому содержащаяся в Р полуокружность с центром на граничной прямой отображается на такую же полуокружность. В модели это означает, что при «отражениях» «прямые» переходят в «прямые». Очевидно, что также «лучи» переходят в «лучи» и «отрезки» — в «отрезки».
Обратимся к откладыванию отрезков и углов в модели. Понятия, относящиеся к модели, будем предварять знаком *.
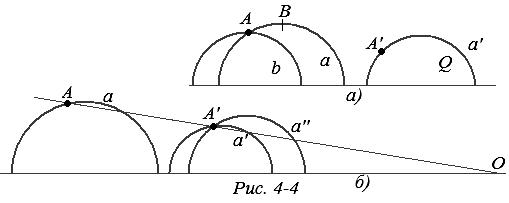
Пусть даны точка А, *луч а с началом А, *отрезок АВ на этом *луче и *угол ab с вершиной А, образованный *лучом а вместе с *лучом b. Пусть даны также точка А', исходящий из нее *луч а', и отмечена * полуплоскость Q, ограниченная *прямой, содержащей *луч а' (рис. 4-4,а). Нам нужно произвести *наложение, переводящее точку А в А’, *луч а — в а' и *луч b — в *луч, лежащий в *полуплоскости Q так, что *угол, *равный ab, отложится от а' в эту *полуплоскость.
Проведем прямую АА', и пусть она пересекает граничную прямую р в точке О (рис. 4-4,б). Произведем инверсию с центром О, которая переведет А в А'. *Луч а перейдет в *луч а" с началом А', он образует с *лучом а' *угол а'а").
Проведем прямую q (без кавычек), делящую *угол а'а" пополам, и построим окружность с центром на граничной прямой, касающуюся прямой q (кстати, укажите такое построение). Инверсия в этой окружности переведет *луч а" в а' (почему?). В смысле модели это значит, что *отражение в соответствующей *прямой переводит *луч а" в а'. Таким образом, два отражения переводят точку А в А' и *луч а — в а'. Вместе с *лучом вся содержащая его *прямая ![]() — полуокружность — переходит в *прямую
— полуокружность — переходит в *прямую ![]() — полуокружность,— содержащую *луч а'. *Полуплоскости, ограниченные *прямой
— полуокружность,— содержащую *луч а'. *Полуплоскости, ограниченные *прямой ![]() , отображаются на *полуплоскости, ограниченные *прямой
, отображаются на *полуплоскости, ограниченные *прямой ![]() . *Луч b, служащий стороной данного *угла ab, переходит в *луч b" с началом А'. Но он может оказаться не в той *полуплоскости, которая была заранее отмечена. Тогда нужно произвести еще *отражение в *прямой, содержащей *луч а', т. е. инверсию в окружности, содержащей эту *прямую. При этом на самой *прямой
. *Луч b, служащий стороной данного *угла ab, переходит в *луч b" с началом А'. Но он может оказаться не в той *полуплоскости, которая была заранее отмечена. Тогда нужно произвести еще *отражение в *прямой, содержащей *луч а', т. е. инверсию в окружности, содержащей эту *прямую. При этом на самой *прямой ![]() ничего не происходит: все ее точки остаются неподвижными. И только *луч b" перейдет в *луч b, лежащий в указанной *полуплоскости.
ничего не происходит: все ее точки остаются неподвижными. И только *луч b" перейдет в *луч b, лежащий в указанной *полуплоскости.
Если на *луче а была отмечена какая-нибудь точка В, и тем самым отмечен *отрезок АВ, то эта точка перейдет в определенную точку В' на *луче а' и *отрезок АВ — в *отрезок А'В' на этом * луче. Так мы получаем результат: на каждом *луче а' можно от его начала отложить *отрезок, *равный данному, т. е. для любого данного *отрезка АВ на данном *луче с началом А' есть такая точка В', что *отрезок АВ можно перевести в *отрезок А'В' путем *наложения.
Совершенно так же то, что *луч b перейдет в *луч b', лежащий в нужной полуплоскости, что и *угол а'b' равен данному ab, позволяет утверждать:
От каждого *луча от его начала по данную сторону от *прямой, его содержащей, можно отложить *угол, равный данному.
Остается доказать, что *угол откладывается единственным образом, так же, как и *отрезок (или, по нашей аксиоме меньшего отрезка, отрезок, содержащийся в данном и не совпадающий с ним, не может быть равен ему).
Утверждение о единственности откладывания угла сводится, очевидно, к следующему:
Если *лучи b, с, исходящие из начала *луча а, образуют с ним равные углы и лежат с одной стороны от него (в одной полуплоскости), то они совпадают.
Но *углы, равные в модели, равны в обычном «евклидовом» смысле, а для обычных углов сказанное, очевидно, верно. *Лучи b, с содержатся в окружностях с центрами на данной прямой р. Раз они образуют с *лучом а данный угол, то, значит, дана касательная к указанным окружностям в точке А. Но окружность с центром на данной прямой, касающаяся другой прямой в данной ее точке, только одна. Значит, *лучи b, с совпадают. Итак, *угол откладывается единственным образом.
*Отрезок, *равный данному, также откладывается на данном *луче единственным образом. Действительно, пусть *отрезок АВ, *равный данному, отложен на данном *луче а с началом А. Если бы можно было отложить другой *отрезок, АС, равный тому же, то это значило бы, что есть *наложение (отличное от тождественного), отображающее *луч сам на себя. Оно отображает тогда на себя и всю содержащую его *прямую — полуокружность а. Если же *наложение переставляет *полуплоскости, ограниченные *прямой а, то добавив отражение в ней, можно добиться того, что и полуплоскости эти будут отображаться каждая на себя.
В таком случае, ввиду сохранения углов, все *лучи, исходящие из точки А, будут отображаться на себя. Значит, при такой композиции инверсий (и отражений в вертикальных лучах) все концы лучей на граничной прямой остаются на месте. Вместе с ними отображаются на себя все полуокружности с концами на граничной прямой, т. е. *прямые модели. Но каждую точку можно получить в пересечении этих *прямых. Поэтому все точки отображаются на себя — «остаются на месте» — так что рассматриваемое *наложение оказывается тождественным вопреки предположению.
Этим единственность откладывания на данном луче отрезка, равного данному, доказана.
На этом доказательство того, что в рассмотренной модели выполняется геометрия Лобачевского, заканчивается. Требование аксиомы меньшего отрезка, что в отрезок нельзя уместить ему равный, заведомо. Выполняется при том, что уже доказано. Впрочем, доказательство того, что оно выполнено, читатель может провести сам.
Описанную модель плоскости Лобачевского можно еще назвать конформной, поскольку в ней наложения представляются инверсиями — преобразованиями, сохраняющими углы.
Модель геометрии Лобачевского в пространстве
Эта модель определяется аналогично модели на плоскости. За пространство принимается открытое полупространство Р. «Плоскостями»» в нем служат содержащиеся в Р полусферы с центрами на граничной плоскости, а также перпендикулярные ей открытые полуплоскости. За «прямые»» принимаются полуокружности, перпендикулярные граничной плоскости (т. е. касательные к ним в концах перпендикуляры этой плоскости; центры их лежат на граничной плоскости), а также перпендикулярные ей лучи. Роль «наложений»» играют композиции инверсий в сферах с центрами на граничной плоскости и отражений в перпендикулярных ей плоскостях.
Модель геометрии Лобачевского на поверхности
Оказывается, что геометрия Лобачевского реализуется на поверхностях постоянной отрицательной кривизной: внутренняя геометрия такой поверхности и есть геометрия Лобачевского. Только не на всей плоскости, а на той ее части, которая может быть представлена данной поверхностью. Вместе с тем доказано, что не существует (в трехмерном евклидовом пространстве) никакой поверхности, которая своей внутренней геометрией представляла бы всю плоскость Лобачевского.
Во внутренней геометрии поверхности роль прямолинейных отрезков играют кратчайшие линии (отрезки геодезических); роль наложений — такие отображения фигур, содержащихся в поверхности, которые сохраняют расстояния, измеряемые по этим кратчайшим линиям.
Самая известная из поверхностей постоянной отрицательной кривизны — псевдосфера — изображена на рис. 4-5.
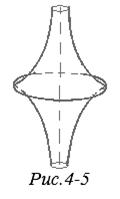
Реализацию геометрии Лобачевского на поверхностях постоянной отрицательной кривизны установил итальянский математик Бельтрами (в 1861 г.).
Впрочем, еще за 30 лет до него это установил, собственно, Миндинг — профессор университета в Дерпте (ныне Тарту), — но не понял этого.
Доказательство логической непротиворечивости геометрии Лобачевского
Мы докажем непротиворечивость системы аксиом планиметрии Лобачевского, состоящей из четырех групп I1-3, II1-4, III1-5, IV1-2 аксиом Гильберта (аксиомы абсолютной планиметрии) и аксиомы V* Лобачевского. При решении этой задачи предполагается, что евклидова геометрия (т. е. система аксиом ∑H Гильберта) непротиворечива. Мы построим из объектов евклидовой плоскости модель плоскости Лобачевского, которая называется евклидовой моделью Кэли — Клейна. Рассмотрим на евклидовой плоскости некоторую окружность ω с центром О радиуса r = 1 и назовем ее абсолютом. Обозначим через Ω круг с границей ω, а через ![]() множество внутренних точек этого круга.
множество внутренних точек этого круга.
Введем следующие соглашения. Неевклидовой точкой назовем любую евклидову точку М![]() , а неевклидовой прямой — любую хорду (без концов) окружности ω. Отношения «принадлежность» и «лежать между» понимаем в обычном смысле. Неевклидовы прямые будем обозначать так: UV, U1V1 и т. д., предполагая, что U, V, U1, V1
, а неевклидовой прямой — любую хорду (без концов) окружности ω. Отношения «принадлежность» и «лежать между» понимаем в обычном смысле. Неевклидовы прямые будем обозначать так: UV, U1V1 и т. д., предполагая, что U, V, U1, V1 ![]() . Таким образом, неевклидовыми точками прямой UV будут те и только те евклидовы точки, которые лежат между точками U и V.
. Таким образом, неевклидовыми точками прямой UV будут те и только те евклидовы точки, которые лежат между точками U и V.
Нетрудно убедиться в том, что при этих соглашениях выполняются все аксиомы I1-3, II1-4 Гильберта. Проверим в качестве примера аксиому. Пусть А и В — две неевклидовы точки, a UV — неевклидова прямая, на которой они лежат. Так как А и В — внутренние точки хорды UV, то на этой хорде существует хотя бы одна внутренняя точка С, такая, что А — В — С. Отсюда мы заключаем, что существует по крайней мере одна неевклидова точка С, такая, что неевклидова точка В лежит между неевклидовыми точками А и С.
Так как в построенной модели выполняются все аксиомы групп I, II Гильберта, то выполняются и все следствия из этих аксиом, в частности имеют место теоремы, с помощью которых вводятся понятия луча и полуплоскости. Ясно, что неевклидовым лучом, исходящим из точки С, является множество всех внутренних точек произвольной полухорды CU окружности ω (CU — евклидов отрезок, где С — внутренняя точка круга Ω, a U — точка на его границе). Неевклидовой полуплоскостью является множество всех внутренних точек какого-нибудь сегмента круга Ω.
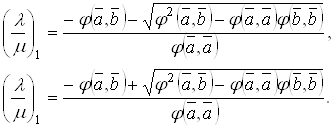
Для того чтобы в нашей модели определить равенство отрезков и углов, введем ряд вспомогательных понятий. Напомним, что на евклидовой плоскости простым отношением трех точек А, В и С, лежащих на одной прямой, называется число (АВ, С) = λ, такое, что ![]() , а сложным отношением четырех точек А, В, С, D, лежащих на одной прямой,— число (АВ, CD) =
, а сложным отношением четырех точек А, В, С, D, лежащих на одной прямой,— число (АВ, CD) = ![]() . Из этого определения непосредственно вытекают следующие свойства.
. Из этого определения непосредственно вытекают следующие свойства.
Похожие работы
... 3. Б.Л. Лаптев. Н.И. Лобачевский и его геометрия. Пособие для учащихся. М. «Просвещение», 1970г. 4. И.М. Яглам. Принцип относительности Галилея и неевклидова геометрия.Серия «Библиотека математического кружка» М: 1963г. Приложение 1 Николай Иванович Лобачевский, второй сын мелкого чиновника, родился 1 декабря(20 ...
... , т. е. такие пары точек считаются за одну точку. Из этого определения следует, что при возрастании n число типов неевклидовых пространств также растет. Неевклидовы геометрии являются геометриями простейших римановых пространств определенной и неопределенной метрики, составляющих так называемый класс пространств постоянной ненулевой кривизны. Каждое из таких n-мерных пространств допускает ...
... метод координат. V. Аксіома паралельності Сама остання аксіома грає в геометрії особливу роль, визначаючи поділ геометрії на дві логічно несуперечливі й взаємно виключають один одного системи: Евклідову й неевклідову геометрії. У геометрії Евкліда ця аксіома формулюється так. V. Нехай а – довільна пряма й А – крапка, що лежить поза прямій а, тоді в площині α, обумовленою крапкою А и ...
... представить другие геометрии Кант счел достаточным основанием, чтобы утверждать, что другие геометрии не могут существовать. Появление неевклидовой геометрии Но многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой, а в ...

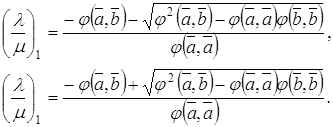
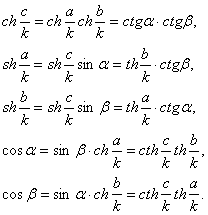
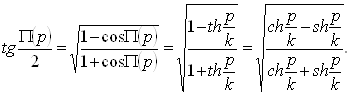
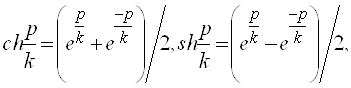
0 комментариев