Навигация
Дифференциальные уравнения
Задача №1
Даны вершины треугольника АВС.
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты CD и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.
А(-7;5), В(5;-4), С(3;10).
Решение
1. Расстояние d между точками M1(x1;у1) и М2(х2;у2) определяется по формуле:
![]()
Подставив в эту формулу координаты точек А и В имеем:
![]()
2. Уравнение прямой, проходящей через точки М1(х1;у1) и М2(х2;у2), имеет вид:
![]()
Подставив в формулу (2) координаты точек А и В, получим уравнение прямой АВ:
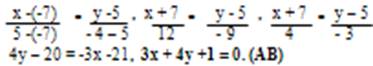
Для нахождения углового коэффициента kab прямой АВ разрешим полученное уравнение относительно у:
![]()
Отсюда
kab = - 3/4.
Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС.
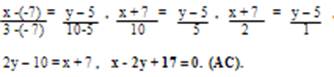
Для нахождения углового коэффициента kaс прямой АС разрешим полученное уравнение относительно у:
![]()
Отсюда
kaс = 1/2.
3. Угол α между двумя прямыми, угловые коэффициенты которых равны k1 и k2, определяется по формуле:
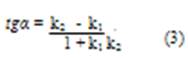
Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее
k1= kab = -3/4, k2 = kac = 1/2.
![]()
< А = arctg 2 = 1,11 рад.
4. Так как высота CD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.
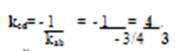
Уравнение прямой, проходящей через данную точку М1(х1;у1) в заданном угловом коэффициенте k имеет вид:
у – у1 = k(х – х1).(4)
Подставив в формулу (4) координаты точки С и kcd = 4/3, получим уравнение высоты CD:
у – 10 = 4/3(х – 3) , у – 10 = 4/3х – 4 , 4х – 3у + 18 = 0. (CD)
Для нахождения длины CD определим координаты точки D, решив систему уравнений (АВ) и (СD):
![]()
Подставив в формулу (1) координаты точек C и D, находим:
![]()
![]() СD= √(-3 -3)2 + (2 -10)2 = √36 + 64 = 10 .
СD= √(-3 -3)2 + (2 -10)2 = √36 + 64 = 10 .
5. Уравнение окружности радиуса R с центром в точке E(a;b) имеет вид:
(х – а)2 + (у – b)2 = R2 (5)
Так как СD является диаметром искомой окружности, то ее центр Е есть середина отрезка CD. Воспользовавшись формулами деления отрезка пополам, получим:
![]()
Следовательно E(0;6) и R = CD/2 = 5. Используя формулу (5), получим уравнение искомой окружности:
(х – 0)2 + (у – 6)2 = 25, х2 + (у – 6)2 = 25.
6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая прямая ВС и содержит точку А, а третья ограничена прямой АС и содержит точку В. Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВ и содержащую точку С, подставим в уравнение прямой АВ координаты точки С:
3* 3+ 4*10 +1 = 50 > 0.
поэтому искомое неравенство имеет вид:
3х + 4у +1 ≥ 0.
Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и содержащую точку А, найдем уравнение прямой ВС, подставив в формулу (2) координаты точек В и С:
![]()
Подставив в последнее уравнение координаты точки А, имеем:
7* (- 7) + 5 – 31 = - 75 < 0.
Искомое неравенство будет
7х + у – 31 ≤ 0.
Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В:
5 – 2(- 4) + 17 = 30 > 0.
Третье искомое неравенство
х – 2у + 17 ≥ 0.
Итак, множество точек треугольника АВС определяется системой неравенств:
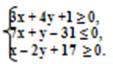
Задача №2
Даны векторы a1 , a2 , a3 , b . Показать, что векторы a1 , a2 , a3 образуют базис трехмерного пространства и найти координаты вектора b в этом базисе.
a1(5;3;1) , а2(-2;-1;2) , а3(-2;1;4) , b(3;0;1)
Решение
1. Система векторов ![]() в пространстве Rn линейно независима тогда и только тогда, когда отличен от нуля определитель, строками (столбцами) которого являются координаты векторов системы:
в пространстве Rn линейно независима тогда и только тогда, когда отличен от нуля определитель, строками (столбцами) которого являются координаты векторов системы:
![]()
![]()
![]()
![]() Подставив в формулу (1) координаты векторов a1 , a2 , a3 найдем определитель:
Подставив в формулу (1) координаты векторов a1 , a2 , a3 найдем определитель:
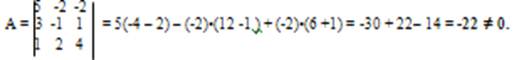
Так как определитель не равен нулю, то данные три вектора являются линейно независимыми. Соответственно они образуют базис трехмерного пространства.
Похожие работы
... условий: y(x0)=y0, . Эти начальные условия дают соответственно n уравнений , , , ……………………………… , решая которые относительно c1, c2 , …, cn находят значения этих постоянных. Например, для дифференциального уравнения 1-го порядка общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую, проходящую через точку M(x0,y0). Геометрическая ...
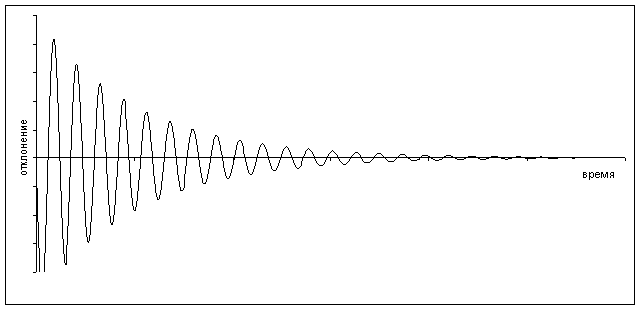
... bo=31,20 Запишем это уравнение в стандартной форме. Для этого разделим (1) на ao: - +y(t)=g(t) -T1 +y(t)=kg(t) (2), где k=-коэффициент передачи, T1=,T22=-постоянные времени. Если корни характеристического уравнения для дифференциального уравнения 2-го порядка комплексные (это выполняется при T1<2T2), то оно является колебательным. Проверим это для нашего уравнения: T1=0,042 2T2=0,14 ...
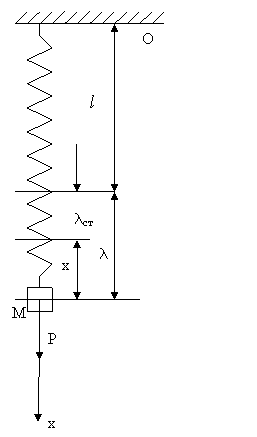
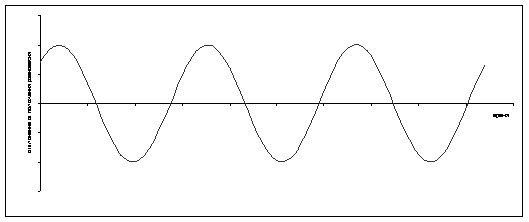
... уравнение в виде: или, обозначив с/m через k2, (1) Полученное уравнение определяет так называемые свободные колебания груза. Оно называется уравнением гармонического осциллятора. Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение: имеет мнимые корни , соответственно этому общее решение Для выяснения ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
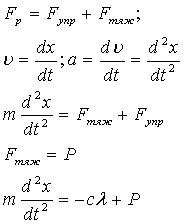
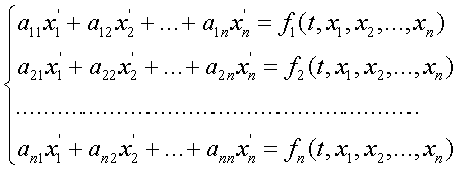
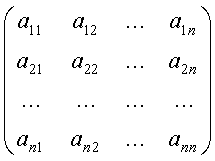
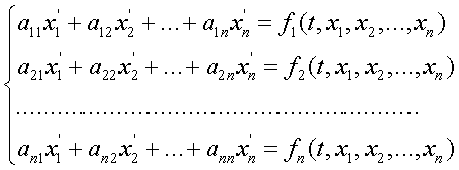
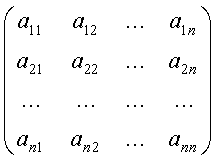
0 комментариев