Навигация
Значение целевой функции в ячейке G6 = 15880;
1. Значение целевой функции в ячейке G6 = 15880;
2. Значения переменных в ячейках B8:D8: х1 = 86, х2 = 0, х3 = 268; это значит, что 1-й продукт должен производиться в объеме 86 единиц, 2-й – 0, а 3-й – 286.
3. Плановый расход ресурсов в ячейках G2:G4: расход 1-го ресурса = 271,6, расход 2-го ресурса = 310, расход 3-го ресурса = 2200.
Как видно 1-й ресурс недоиспользован, а 2-й и 3-й израсходованы полностью.
Кроме результатов в электронной таблице EXCEL готовит три отчета: Результаты, Устойчивость, Пределы. Отчет по результатам изображен на рис 4.1.5, где изображены три таблицы.
Отчет по результатам
Целевая ячейка (максимум)
Ячейка Имя Исходно Результат
$G$6 Цены ЦФ 15880
Изменяемые Ячейки
| Ячейка Имя Исходно Результат |
| $B$8 Перем Пр1 0 86 |
| $C$8 Перем Пр2 0 0 |
| $D$8 Перем Пр3 0 268 |
Ограничения
| Ячейка Имя Значение Формула Статус Разница |
| $G$2 Рес 1 Расход 271,6 $G$2 |
| $G$3 Рес 2 Расход 310 $G$3 |
| $G$4 Рес 3 Расход 2200 $G$4 |
| $B$8 Перем Пр1 86 $B$8 |
| $C$8 Перем Пр2 0 $C$8 |
| $D$8 Перем Пр3 268 $D$8 |
Рис. 4.1.5
1-я таблица – целевая ячейка – дает значение целевой функции, которая уже имеется в таблице EXCEL, значит, эти данные избыточны.
2-я таблица – изменяемые ячейки – дает значение переменных, которые уже имеются в таблице EXCEL, эти данные тоже избыточны.
3-я таблица – ограничения – дает оценку ограничений. Колонка «значение» дает значения планового расхода ресурсов и переменных – эти данные имеются в таблице EXCEL и здесь избыточны. Столбец «статус» значением «связанное» отмечает ограничения (не больше или не меньше), которые в результате решения превратились в строгие равенства, прочие ограничения имеют статус «несвязанные». Столбец «разница» показывает, на какую величину ограничения отклонились от строгого равенства. Так, например, ограничение 1-го ресурса 500, плановое значение 271,6, разница = 500 – 271,6 = 228,4.
Отчет по устойчивости изображен на рис. 4.1.6. Он состоит из двух таблиц.
Отчет по устойчивости
Изменяемые ячейки
| Ячейка Имя Результат Норир. Значение градиент |
| $B$8 Перем Пр1 86 0 |
| $C$8 Перем Пр2 0 -22,8 |
| $D$8 Перем Пр3 268 0 |
Ограничения
| Ячейка Имя Результат. Лагранжа значение Множитель |
| $G$2 Рес 1 Расход 271,6 0 |
| $G$3 Рес 2 Расход 310 20 |
| $G$4 Рес 3 Расход 2200 4,4 |
Рис. 4.1.6
Таблица «изменяемые ячейки» показывает значения переменных, которые уже имеются в таблице EXCEL. Столбец «нормируемый градиент» показывает, как влияет увеличение переменных на единицу на величину целевой функции. Таблица «ограничения» содержит важную информацию в столбце «Лагранжа множители». Эти величины в литературе имеют различные названия: объективно обусловленные оценки (О.О.О.) по Л. Канторовичу, двойственные оценки по Д. Данцигу, оптимальные цены, теневые цены и другие. В дальнейшем будем называть их наиболее распространенным именем – двойственные оценки и обозначать – vi, где i – номер ограничения. В данном примере v1 = 0, v2 = 20,0, v3 = 4,4. Отчет по пределам показан на рис. 4.1.7.
Отчет по пределам
| Ячейка Целевое Значение имя |
| $G$6 Цены ЦФ 15880 |
| Ячейка Изменяемое Значение имя | Нижний Целевой предел результат | Нижний Целевой предел результат |
| $B$8 Перем Пр1 86 | 0 10720 | 86 15880 |
| $C$8 Перем Пр2 0 | 0 15880 | 0 15880 |
| $D$8 Перем Пр3 268 | 0 5160 | 268 15880 |
Рис. 4.1.7.
В этом отчете уже в третий раз дается значение целевой функции 15880, в пятый раз значение переменных (х1 = 86, х2 = 0, х3 = 268). Нижний предел для всех переменных = 0, так, установлены ограничения по переменным. Верхний предел равен соответственно 86, 0 и 268, так устанавливают ограничения по ресурсам. Целевой результат показывает значение целевой функции при соответствующих значениях переменных. Если х1 = 0, то ЦФ = 10720 и т.д.
Запишем математическую модель рассмотренной задачи в общем виде:
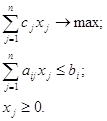
Пусть:
В-бюджет, т.е. количество денег, которое можно израсходовать на приобретение ресурсов для производства продукции, а si – рыночная цена i-го ресурса. Тогда единственное ограничение по ресурсам будет выглядеть следующим образом:
![]() .
.
Смысл этого ограничения - нельзя израсходовать ресурсов на сумму больше, чем В.
Здесь: ![]() - расход i-го ресурса в натуральном выражении по j-му технологическому способу;
- расход i-го ресурса в натуральном выражении по j-му технологическому способу;
![]() - расход i-го ресурса в натуральном выражении по всем способам;
- расход i-го ресурса в натуральном выражении по всем способам;
![]() - суммарная цена i-го ресурса, израсходованного по всем способам;
- суммарная цена i-го ресурса, израсходованного по всем способам;
![]() - суммарная цена всех ресурсов по всем технологическим способам.
- суммарная цена всех ресурсов по всем технологическим способам.
Решим задачу на максимум продукции с ограничением по бюджету. За основу возьмем электронную модель на рис. 4.1.3. и дополним ценами ресурсов si и бюджетом В (рис. 4.1.8)
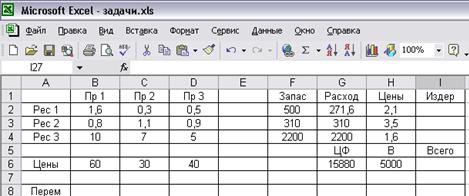
Рис. 4.1.8
Дополнительные величины:
H2:H4 – цены ресурсов (задаются);
I2:I4 – издержки (вычисляются);
I2 = G2*H2;
I3:I4 – копируется из I2;
H6 = 5000 – бюджет (задается);
I6 – издержки всего (вычисляются);
I6 = СУММ (I2:I4).
Ограничения:
B8:D8 ![]() 0 – неотрицательности переменных;
0 – неотрицательности переменных;
I6 ![]() H6 – совокупные издержки не больше бюджета.
H6 – совокупные издержки не больше бюджета.
Будет получено решение
x1 = 0; x2 = 0; x3 = 409,84.
v = 3,08 – двойственная оценка ограничения по бюджету – увеличение бюджета на единицу увеличивает валовой продукт на 3,28.
Если ограничения по ресурсам в модели имеют смысл и не больше (![]() ) и не меньше (
) и не меньше (![]() ), причем все величины (
), причем все величины (![]() ) не отрицательные, то в общем случае вывод о существовании или отсутствии допустимого плана сделать нельзя. Все зависит от конкретных значений величин
) не отрицательные, то в общем случае вывод о существовании или отсутствии допустимого плана сделать нельзя. Все зависит от конкретных значений величин ![]() и
и ![]() . Возможен случай, когда для некоторого k-го ресурса установлено такое ограничение
. Возможен случай, когда для некоторого k-го ресурса установлено такое ограничение ![]() , что оно не может быть выполнено из-за других ограничений. Тогда нет ни одного допустимого плана.
, что оно не может быть выполнено из-за других ограничений. Тогда нет ни одного допустимого плана.
Заключение
В результате проделанной работы был рассмотрен теоретический материал, посвященный решению двойственных задач линейного программирования, и процесс их решения был автоматизирован, с помощью программы MS Excel.
Результатом работы над курсовым проектом является программа для решения задач линейного программирования с помощью двойственного симплекс-метода.
Список используемой литературы
1. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. «Наука», 1980 г.
2. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. «Финансы и статистика», 1998 г.
3. Математическое моделирование в задачах. Белолипецкий В.М., Шокин Ю.И.
4. Математическое Белолипецкий В.М.
Похожие работы
... , доставляющий наибольшее значение целевой функции по сравнению с любым другим допустимым вектором , т.е. , называется решением задачи, или оптимальным планом. Максимальное значение целевой функции называется значением задачи. Двойственная задача линейного программирования. Рассмотрим задачу ЛП (1) или, в матричной записи, (2) Задачей, двойственной к (1) (двойственной задачей), называется ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... . 1.3. Построение ограничений и градиента целевой функции : 1.4. Область допустимых решений – отрезок AB. 1.5. Точка А – оптимальная. Координаты т. А: ; ; . 2. Решение задачи линейного программирования симплекс-методом. Прямая задача. Задачу линейного программирования для любой вершины в компактной форме можно представить в виде: Для получения используем алгоритм, приведённый в ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
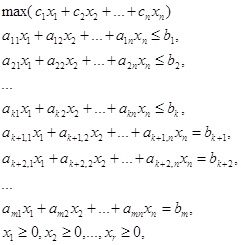
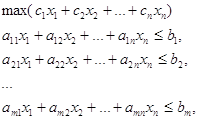
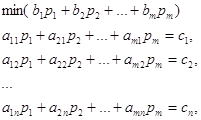





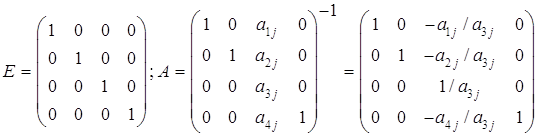
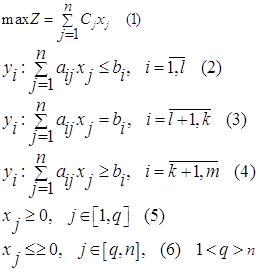
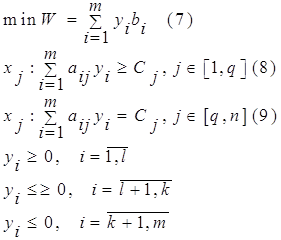
0 комментариев