Способ пропорционального деления и долевого участия

5. Способ пропорционального деления и долевого участия

В ряде случаев для определения величины влияния факторов
на прирост результативного показателя может быть использован
способ пропорционального деления. Это касается тех случаев,
когда мы имеем дело с аддитивными моделями типа Y = ∑Xi и сме­шанными типа

Y=a/(b+c+d+…+n) (50)

В первом случае, когда имеем одноуровневую модель типа У = а + b + с, расчет проводится следующим образом:

∆Ya=∆Y/(∆a+∆b+∆c)*∆a  (51)

∆Yb=∆Y/(∆a+∆b+∆c)*∆b  (52)

∆Yc=∆Y/(∆a+∆b+∆c)*∆c (53)

Методика расчета для смешанных моделей несколько сложнее.
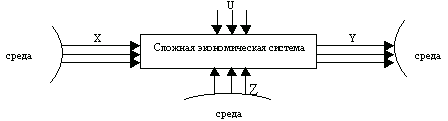
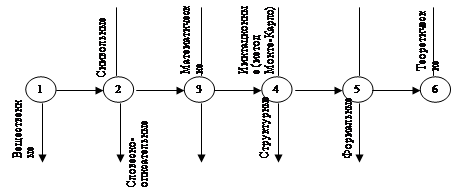
Взаимосвязь факторов в комбинированной модели показана на
рис. 1.1

Рис. 1.1 Взаимосвязь факторов в комбинированной модели

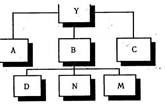-  Результативный показатель

-  Факторы первого уровня

-Факторы второго уровня

Когда известны ∆B_d; ∆В_п и ∆В_т, а также ∆Y_b, то для определе­ния ∆Y_d, ∆Y_n, ∆Y_m можно использовать способ пропорциональ­ного деления, который основан на пропорциональном распределении прироста результативного показателя Y за счет изменения фактора B между факторами второго уровня D, N и М соответственно их величине. Пропорциональность этого распределения достигается пу­тем определения постоянного для всех факторов коэффициента, ко­торый показывает величину изменения результативного показателя Y за счет изменения фактора B на единицу.

Величина коэффициента (К) определяется следующим образом:

K= ∆Yb/∆Bобщ= ∆Yb/(∆Bd+∆Bn+∆Bm) (54)

Умножив этот коэффициент на абсолютное отклонение B за счет соответствующего фактора, найдем отклонения результативного по­казателя:

Для решения такого типа задач можно использовать также спо­соб долевого участия. Для этого сначала определяется доля каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя

∆Ya=∆a/(∆a+∆b+∆c)* ∆Yобщ (58)

∆Yb=∆b/(∆a+∆b+∆c)* ∆Yобщ (59)

∆Yc=∆c/(∆a+∆b+∆c)* ∆Yобщ (60)

Аналогичных примеров применения этого способа в АХД можно привести очень много, в чем можно убедиться в процессе изу­чения отраслевого курса анализа хозяйственной деятельности на предприятиях.

6.Интегральный способ в анализе хозяйственной деятельности

Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом же деле они изменяются совместно, взаимосвязано и от этого взаимодействия получается дополнительный прирост результативного показателя, который при применении способов элиминирования присоединяется к одному из факторов, как правило, к последнему. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от места, на которое поставлен тот или иной фактор в детерминированной модели.

Интегральный способ применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях типа

Y=F/∑Xi

Исполь­зование этого способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной под­становки, абсолютных и относительных разниц и избежать неодно­значной оценки влияния факторов потому, что в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, который обра­зовался от взаимодействия факторов, раскладывается между ними пропорционально изолированному их воздействию на результатив­ный показатель.

На первый взгляд может показаться, что для распределения допол­нительного прироста достаточно взять его половину или часть, соот­ветствующую количеству факторов. Но это сделать чаще всего сложно, так как факторы могут действовать в разных направлениях. Поэтому в интегральном методе пользуются определенными фор­мулами. Приведем основные из них для разных моделей.

1. F=XY

 ∆Fx=∆XYo+1/2∆X∆Y; или ∆Fx=1/2∆X(Yo+Y1) (61,61.2)

∆Fy=∆YXo+1/2∆X∆Y; или ∆Fy=1/2∆Y(Xo+X1) (62,62.2)

∆Fx=1/2∆X(YoZ1+Y1Zo)+1/3∆X∆Y∆Z (63)

∆Fy=1/2∆Y(XoZ1+X1Zo)+1/3∆X∆Y∆Z  (64)

∆Fz=1/2∆Z(XoY1+X1Yo)+1/3∆X∆Y∆Z (65)

Похожие работы

Классификация математических моделей, используемых в экономике и менеджменте

Скачать

75818

3

7

... параметрами, показателями объекта именно в то время. Дискретные модели отображают состояние объекта управления в отдельные, фиксированные моменты времени. Имитационными называют экономико-математические модели, используемые с целью имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники. По типу математического аппарата, применяемого в ...

Методы сравнительного анализа деятельности посреднических предприятий

Скачать

26043

2

0

... товара (выбор методов продажи, организация обслуживания покупателей, осуществление мероприятий по созданию привлекательной атмосферы торгового зала). 3. МЕТОДЫ СРАВНИТЕЛЬНОГО АНАЛИЗА ДЕЯТЕЛЬНОСТИ ПОСРЕДНИЧЕСКИХ ПРЕДПРИЯТИЙ Методики сравнительного анализа деятельности посредников представлены различными авторами и имеют отличительные компоненты и структуру. Методика таких анализов необходима ...

Методы детерминированного и стохастического факторного анализа

Скачать

29465

3

7

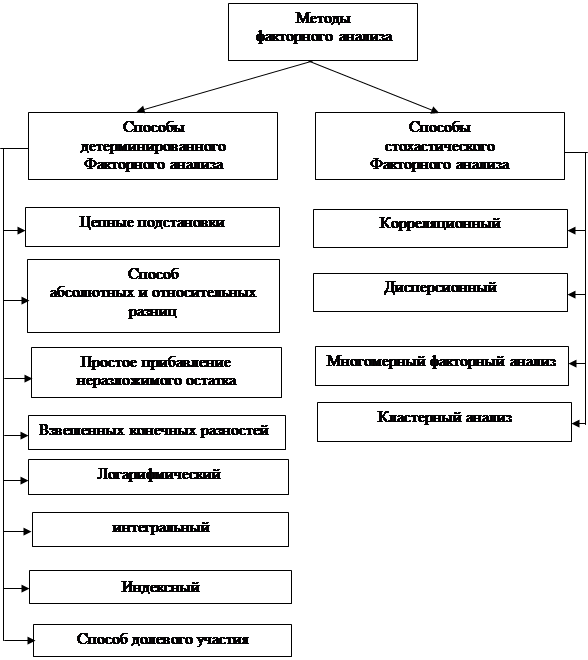
... определённое статистическое распределение) – стохастическая (вероятностная) связь. Соответственно типу связи аналитические приёмы и способы делятся на методы детерминированного факторного анализа и методы стохастического факторного анализа. 2. Задачи факторного анализа. Рассмотрим примерную классификацию задач факторного анализа работы предприятий с точки зрения использование математических ...

Экономико-математическое моделирование

Скачать

51386

5

18

... ai- расход сырья на единицу продукции; B - общий запас сырья; W - область допустимых ограничений; Тема 2. Метод математического моделирования в экономике. 2.1. Понятие “модель” и “моделирование”. С понятием “моделирование экономических систем” (а также математических и др.) связаны два класса задач: 1)            задачи анализа, когда система подвергается глубокому изучению ее ...