Навигация
F=XYZG
3. F=XYZG
∆Fx=1/6∆X{3YoZoGo+Y1Go(Z1+∆Z)+G1Zo(Y1+∆Y)+Z1Yo(G1+∆G)}+
+1/4∆X∆Y∆Z∆G (66)
∆Fy=1/6∆Y{3XoZoGo+X1Go(Z1+∆Z)+G1Zo(X1+∆X)+Z1Xo(G1+∆G)}+
+1/4∆X∆Y∆Z∆G (67)
∆Fz=1/6∆Z{3XoZoGo+G1Xo(Y1+∆Y)+Y1Go(X1+∆X)+X1Yo(G1+∆G)}+
+1/4∆X∆Y∆Z∆G (68)
∆Fg=1/6∆G{3XoZoGo+Z1Xo(Y1+∆Y)+Y1Go(X1+∆X)+X1Yo(Z1+∆Z)}+
+1/4∆X∆Y∆Z∆G (69)
Для расчета влияния факторов в кратных и смешанных моделях используются следующие рабочие формулы.
1. Вид факторной модели:
F=X/Y
∆Fx=(∆X/∆Y)ln│Y1/Yo│ (70)
∆Fy=∆Fобщ-∆Fx (71)
2. Вид факторной модели:
F=X/(Y+Z)
∆Fx=(∆X/(∆Y+∆Z)) ln│(Y1+Z1)/(Yo+Zo)│ (72)
∆Fy=((∆Fобщ-∆Fx)/(∆Y+∆Z))* ∆Y (73)
∆Fz=((∆Fобщ-∆Fx)/(∆Y+∆Z))* ∆Z (74)
3. Вид факторной модели:
F=X/(Y+Z+G)
∆Fx=(∆X/(∆Y+∆Z+∆G)) ln│(Y1+Z1+G1)/(Yo+Zo+Go)│ (75)
∆Fy=((∆Fобщ-∆Fx)/(∆Y+∆Z+∆G))* ∆Y (76)
∆Fz=((∆Fобщ-∆Fx)/(∆Y+∆Z+∆G))* ∆Z (77)
∆Fg=((∆Fобщ-∆Fx)/(∆Y+∆Z+∆G))* ∆G (78)
![]()
![]() Таким образом, использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и сделать не очень сложные расчеты с помощью калькулятора или другой вычислительной техники. [1,стр.110)
Таким образом, использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и сделать не очень сложные расчеты с помощью калькулятора или другой вычислительной техники. [1,стр.110)
7. Способ логарифмирования в анализе хозяйственной деятельности
Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае результат расчета, как и при интегрировании, не зависит от месторасположения факторов в модели и по сравнению с интегральным методом обеспечивается более высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В этом его преимущество, а недостаток - в ограниченности сферы его применения.
В отличие от интегрального метода при логарифмировании используются не абсолютные приросты результативных показателей, а индексы их роста (снижения).
Математически этот метод описывается следующим образом. Допустим, что результативный показатель можно представить в виде произведения трех факторов:
f=xyz (79)
Прологарифмировав обе части равенства, получим:
lgf=lgx+lgy+lgz (80)
Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, произведем замену абсолютных их значений на индексы:
lg(f1:fo)=lg(x1:xo)+lg(y1:yo)+lg(z1:zo) (81)
или
lgIf=lgIx+lgIy+lgIz (82)
Разделив обе части равенства на lgIf и умножив на ∆f получим:
∆f=∆f(lgIx/lgIf)+∆f(lgIy/lgIf)+∆f(lgIz/lgIf)= ∆fx+∆fy+∆fz (83)
Отсюда влияние факторов определяется следующим образом:
∆fx=∆f(lgIx/lgIf) (84)
∆fy=∆f(lgIy/lgIf) (85)
∆fz=∆f(lgIz/lgIf) (86)
Из формул вытекает, что общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму результативного показателя. И не имеет значения, какой логарифм используется - натуральный или десятичный [1].
Рассмотрев основные приёмы детерминированного факторного анализа и сферу их применения, результаты можно систематизировать в виде следующей матрицы [1,стр.112):
| мультипликативные | аддитивные | кратные | смешанные | |
| цепной подстановки | + | + | + | + |
| индексный | + | - | + | - |
| абсолютных разниц | + | - | - | Y=a(b-c) |
| относительных разниц | + | - | - | - |
| долевого участия | - | + | - | Y=a/ |
| интегральный | + | - | + | Y=a/ |
| логарифмирования | + | - | - | - |
В детерминированном факторном анализе можно выделить четыре типовые задачи:
1. Оценка влияния относительного изменения факторов на относительное изменение результативного показателя.
2. Оценка влияния абсолютного изменения i-го фактора на абсолютное изменение результативного показателя.
3. Определение отношения величины изменения результативного показателя, вызванного изменением i-го фактора, к базовой величине результативного показателя.
4. Определение доли абсолютного изменения результативного показателя, вызванного изменением i-го фактора, в общем изменении результативного показателя.
Охарактеризуем эти задачи и рассмотрим решение каждой из них на конкретном простом примере. [7]
Пример.
Объем валовой продукции (ВП) зависит от двух основных факторов первого уровня: численности работников (ЧР) и среднегодовой выработки (ГВ). Имеем двухфакторную мультипликативную модель:
ВП=ЧР*ГВ (87)
Рассмотрим ситуацию, когда и выработка, и численность рабочих в отчетном периоде отклонились от запланированных значений. Данные для расчетов приведены в таблице 1.1.
Таблица 1.1
Данные для факторного анализа объема валовой продукции.
| Показатель | Условное обозначение | План | Факт | Отклонение |
| Валовая продукция, млн. руб. | ВП | 160 000 | 240 000 | 80 000 |
| Среднегодовая численность рабочих, чел. | ЧР | 1000 | 1200 | +200 |
| Среднегодовая выработка одного рабочего, млн. руб. | ГВ | 160 | 200 | +40 |
Задача 1.
Задача имеет смысл для мультипликативных и кратных моделей. Рассмотрим простейшую двухфакторную модель
p=a*b (88)
Очевидно, что при анализе динамики этих показателей будет выполняться следующее соотношение между индексами:
Ip=Ia*Ib (89)
где значение индекса находится отношением значения показателя в отчетном периоде к базисному.
Рассчитаем индексы валовой продукции, численности работников и среднегодовой выработки для нашего примера:
![]() ; (90)
; (90)
![]() . (91)
. (91)
Согласно вышеприведенному правилу, индекс валовой продукции равен произведению индексов численности работников и среднегодовой выработки, т. е.
![]() . (92)
. (92)
Очевидно, что если мы рассчитаем непосредственно индекс валовой продукции, то получим, то же самоe значениe:
![]() . (93)
. (93)
Мы можем сделать вывод: в результате увеличения численности работников в 1,2 раза и увеличения среднегодовой выработки в 1,25 раза объем валовой продукции увеличился в 1,5 раза.
Таким образом, относительные изменения факторных и результативного показателей связаны той же зависимостью, что и показатели в исходной модели. Данная задача решается при ответе на вопросы типа: "Что будет, если i-й показатель изменится на n%, а j-й показатель изменится на k%?".
Задача 2.
Является основной задачей детерминированного факторного анализа; ее общая постановка имеет вид:
Пусть ![]() - жестко детерминированная модель, характеризующая изменение результативного показателя y от n факторов; все показатели получили приращение
- жестко детерминированная модель, характеризующая изменение результативного показателя y от n факторов; все показатели получили приращение ![]() (например, в динамике, по сравнению с планом, по сравнению с эталоном):
(например, в динамике, по сравнению с планом, по сравнению с эталоном):
![]() ;
; ![]() . (94,95)
. (94,95)
Требуется определить, какой частью приращение результативного показателя y обязано приращению i-го фактора, т. е. расписать следующую зависимость:
![]() , (96)
, (96)
где ![]() - общее изменение результативного показателя, складывающееся под одновременным влиянием всех факторных признаков;
- общее изменение результативного показателя, складывающееся под одновременным влиянием всех факторных признаков;
![]() - изменение результативного показателя под влиянием только фактора
- изменение результативного показателя под влиянием только фактора ![]()
Задача 3.
Является в определенном смысле следствием второй типовой задачи, поскольку базируется на полученном факторном разложении. Необходимость решения этой задачи обусловлена тем обстоятельством, что элементы факторного разложения составляют абсолютные величины, которые трудно использовать для пространственно-временных сопоставлений. При решении задачи 3 факторное разложение дополняется относительными показателями:
![]() (97)
(97)
Экономическая интерпретация: коэффициент ![]() показывает, на сколько процентов к базисному уровню изменился результативный показатель под влиянием i-го фактора.
показывает, на сколько процентов к базисному уровню изменился результативный показатель под влиянием i-го фактора.
Рассчитаем коэффициенты α для нашего примера, используя факторное разложение, полученное ранее методом цепных подстановок:
![]() ; (98)
; (98)
![]() . (99)
. (99)
Таким образом, объем валовой продукции повысился на 20% за счет увеличения численности рабочих и на 30% за счет увеличения выработки. Суммарный прирост валовой продукции составил 50%.
Задача 4.
Также решается на основе базовой задачи 2 и сводится к расчету показателей:
![]()
(100)
Экономическая интерпретация: коэффициент ![]() показывает долю прироста результативного показателя, обусловленную изменением i-го фактора. Здесь не возникает вопроса, если все факторные признаки изменяются однонаправлено (либо возрастают, либо убывают). Если это условие не выполняется, решение задачи может быть осложнено. В частности, в наиболее простой двухфакторной модели в подобном случае расчет по приведенной формуле не выполняется и считается, что 100% прироста результативного показателя обусловлены изменением доминирующего факторного признака, т. е. признака, изменяющегося однонаправлено с результативным показателем.
показывает долю прироста результативного показателя, обусловленную изменением i-го фактора. Здесь не возникает вопроса, если все факторные признаки изменяются однонаправлено (либо возрастают, либо убывают). Если это условие не выполняется, решение задачи может быть осложнено. В частности, в наиболее простой двухфакторной модели в подобном случае расчет по приведенной формуле не выполняется и считается, что 100% прироста результативного показателя обусловлены изменением доминирующего факторного признака, т. е. признака, изменяющегося однонаправлено с результативным показателем.
Рассчитаем коэффициенты γ для нашего примера, используя факторное разложение, полученное методом цепных подстановок:
![]() ; (101)
; (101)
![]() . (102)
. (102)
Таким образом, увеличение численности работников обусловило 40% общего повышения объема валовой продукции, а увеличение выработки - 60%. Значит, увеличение выработки в данной ситуации является определяющим фактором [7].
В зависимости от того, какой метод анализа модели выбран, факторныe разложения могут различаться.
Глава 2. Применение детерминированных экономико-математических моделей и методов факторного анализа на примере РУП «ГЗЛиН».
Похожие работы
... параметрами, показателями объекта именно в то время. Дискретные модели отображают состояние объекта управления в отдельные, фиксированные моменты времени. Имитационными называют экономико-математические модели, используемые с целью имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники. По типу математического аппарата, применяемого в ...
... товара (выбор методов продажи, организация обслуживания покупателей, осуществление мероприятий по созданию привлекательной атмосферы торгового зала). 3. МЕТОДЫ СРАВНИТЕЛЬНОГО АНАЛИЗА ДЕЯТЕЛЬНОСТИ ПОСРЕДНИЧЕСКИХ ПРЕДПРИЯТИЙ Методики сравнительного анализа деятельности посредников представлены различными авторами и имеют отличительные компоненты и структуру. Методика таких анализов необходима ...
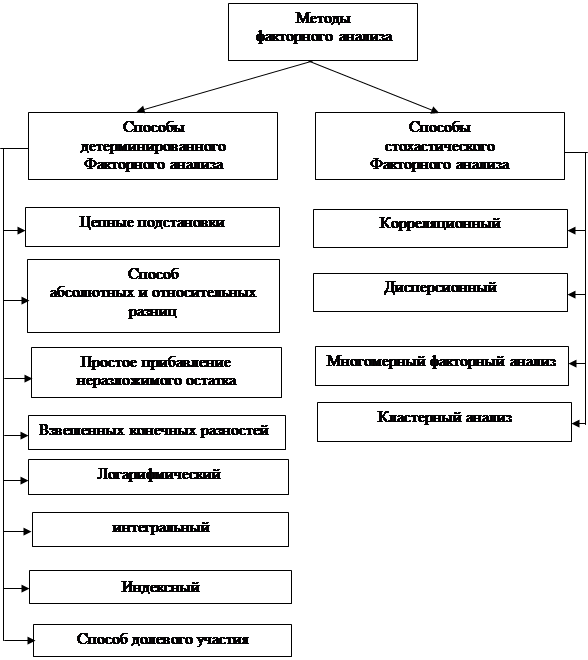
... определённое статистическое распределение) – стохастическая (вероятностная) связь. Соответственно типу связи аналитические приёмы и способы делятся на методы детерминированного факторного анализа и методы стохастического факторного анализа. 2. Задачи факторного анализа. Рассмотрим примерную классификацию задач факторного анализа работы предприятий с точки зрения использование математических ...
... ai- расход сырья на единицу продукции; B - общий запас сырья; W - область допустимых ограничений; Тема 2. Метод математического моделирования в экономике. 2.1. Понятие “модель” и “моделирование”. С понятием “моделирование экономических систем” (а также математических и др.) связаны два класса задач: 1) задачи анализа, когда система подвергается глубокому изучению ее ...

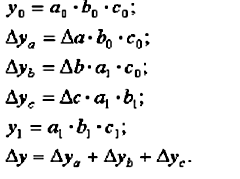

0 комментариев