Навигация
2 вопрос
Автокорреляция - статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом по времени.
Автокоррелированность ряда можно наблюдать, когда нарушено третье условие Гаусса-Маркова, т.е. условие независимости - ![]() .
.
Чем дальше наблюдения друг от друга, тем меньше они коррелируют. Наиболее всего коррелируют соседние наблюдения.
Для проверки рядов на автокорреляцию первого порядка применяется критерий широко известной статистики Дарбина - Уотсона. (DW)
DW = 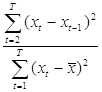
Можно показать, что в больших выборках имеет место сходимость
![]()
Поскольку справедливы неравенства -1 ≤ ρ ≤ 1, то значение статистики DW при больших Т будет находиться в интервале 0 ≤ DW ≤ 4.
Если автокорреляция отсутствует (ρ = 0), то значение DW будет близким к двум.
Если автокорреляция положительна, то DW < 2, если автокорреляция отрицательна, то DW > 2.
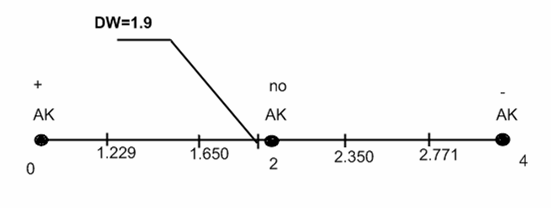
Статистика DW используется для проверки гипотезы Н0 : ρ = 0 против альтернативы Н1 : ρ > 0 или альтернативы Н1 : ρ < 0. Для статистики Дарбина – Уотсона критическое значение d* такое, что в случае DW > d* гипотеза Н0 принимается, как «определить невозможно». Это значение зависит от всей матрицы Х (матрицы наблюдаемых параметров). Однако Дарбин и Уотсон доказали, что существуют две границы, обычно обозначаемые dU и dL (причем dU > dL), которые зависят только от длины рядов, количества объясняющих переменных и уровня значимости, и такие, что dL < d* < dU. Интервал [dL; dU] называется зоной неопределенности. Итоговая методика представлена мною в виде рисунка:
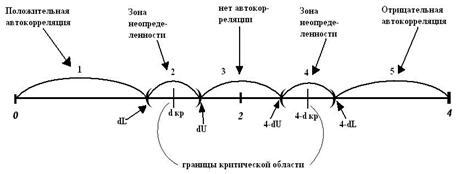
1) 0 < DW < dL – присутствует положительная автокорреляция;
2) dL < DW < dU – область неопределенности;
3) dU < DW < 4 – dU – автокорреляция отсутствует;
4) 4 – dU < DW < 4 – dL - область неопределенности;
5) 4 – dL < DW < 4 – присутствует отрицательная автокорреляция.
В моей работе требовалось проверить ряд зависимой переменной W на автокоррелированность.
Исходный ряд W | ∆ W |
| Остатки U трендовой модели анализа | ∆ U для трендовой модели анализа |
| 434,10000 | 405,94396 | 28,15604 | ||
| 587,90000 | 153,80000 | 477,0841018 | 110,81590 | 82,65986 |
| 545,30000 | -42,60000 | 548,2242436 | -2,92424 | -113,74014 |
| 763,20000 | 217,90000 | 619,3643853 | 143,83561 | 146,75986 |
| 727,10000 | -36,10000 | 690,5045271 | 36,59547 | -107,24014 |
| 714,20000 | -12,90000 | 761,6446689 | -47,44467 | -84,04014 |
| 883,20000 | 169,00000 | 832,7848107 | 50,41519 | 97,85986 |
| 879,00000 | -4,20000 | 903,9249524 | -24,92495 | -75,34014 |
| 930,00000 | 51,00000 | 975,0650942 | -45,06509 | -20,14014 |
| 1354,00000 | 424,00000 | 1046,205236 | 307,79476 | 352,85986 |
| 1102,00000 | -252,00000 | 1117,345378 | -15,34538 | -323,14014 |
| 1834,00000 | 732,00000 | 1188,48552 | 645,51448 | 660,85986 |
| 906,11000 | -927,89000 | 1259,625661 | -353,51566 | -999,03014 |
| 1183,06600 | 276,95600 | 1330,765803 | -147,69980 | 205,81586 |
| 1361,49500 | 178,42900 | 1401,905945 | -40,41094 | 107,28886 |
| 1339,20400 | -22,29100 | 1473,046087 | -133,84209 | -93,43114 |
| 1726,67000 | 387,46600 | 1544,186228 | 182,48377 | 316,32586 |
| 1246,91200 | -479,75800 | 1615,32637 | -368,41437 | -550,89814 |
| 1170,78100 | -76,13100 | 1686,466512 | -515,68551 | -147,27114 |
| 1743,18500 | 572,40400 | 1757,606654 | -14,42165 | 501,26386 |
| 1933,86000 | 190,67500 | 1828,746795 | 105,11320 | 119,53486 |
| 2249,20900 | 315,34900 | 1899,886937 | 349,32206 | 244,20886 |
| 2519,10500 | 269,89600 | 1971,027079 | 548,07792 | 198,75586 |
| 1814,02300 | -705,08200 | 2042,167221 | -228,14422 | -776,22214 |
| 1123,63300 | -690,39000 | 2113,307363 | -989,67436 | -761,53014 |
| 3077,96600 | 1954,33300 | 2184,447504 | 893,51850 | 1883,19286 |
| 2558,11600 | -519,85000 | 2255,587646 | 302,52835 | -590,99014 |
| 3249,06600 | 690,95000 | 2326,727788 | 922,33821 | 619,80986 |
| 2155,53500 | -1093,53100 | 2397,86793 | -242,33293 | -1164,67114 |
| 1817,58500 | -337,95000 | 2469,008071 | -651,42307 | -409,09014 |
| 2436,77600 | 619,19100 | 2540,148213 | -103,37221 | 548,05086 |
| 2153,27700 | -283,49900 | 2611,288355 | -458,01135 | -354,63914 |
| 1417,66800 | -735,60900 | 2682,428497 | -1264,76050 | -806,74914 |
| 1918,29100 | 500,62300 | 2753,568638 | -835,27764 | 429,48286 |
| 2732,59700 | 814,30600 | 2824,70878 | -92,11178 | 743,16586 |
| 3900,56000 | 1167,96300 | 2895,848922 | 1004,71108 | 1096,82286 |
| 2611,58000 | -1288,98000 | 2966,989064 | -355,40906 | -1360,12014 |
| 2665,21000 | 53,63000 | 3038,129206 | -372,91921 | -17,51014 |
| 4307,07000 | 1641,86000 | 3109,269347 | 1197,80065 | 1570,71986 |
| 3286,84000 | -1020,23000 | 3180,409489 | 106,43051 | -1091,37014 |
| 3800,29000 | 513,45000 | 3251,549631 | 548,74037 | 442,30986 |
| 1782,05000 | -2018,24000 | 3322,689773 | -1540,63977 | -2089,38014 |
| 3131,94000 | 1349,89000 | 3393,829914 | -261,88991 | 1278,74986 |
| 2457,14000 | -674,80000 | 3464,970056 | -1007,83006 | -745,94014 |
| 4883,67000 | 2426,53000 | 3536,110198 | 1347,55980 | 2355,38986 |
| 5774,59400 | 890,92400 | 3607,25034 | 2167,34366 | 819,78386 |
| 3318,55300 | -2456,04100 | 3678,390482 | -359,83748 | -2527,18114 |
| 3223,76300 | -94,79000 | 3749,530623 | -525,76762 | -165,93014 |
1. Статистика Дарбина – Уотсона для исходного ряда W:
DW = ![]() = 0,568043736
= 0,568043736
Из таблицы значений констант Дарбина – Уотсона dU и dL на 5% уровне значимости с одним влияющим фактором при Т = 48 находим dL = 1,50; dU = 1,59.
Вывод: так как DW = 0,568043736 < 1,50 = dL, то делаем вывод о наличии в ряде W положительной автокорреляции.
С помощью построения модели линейного тренда постараемся избавиться от автокорреляции.
Модель линейного тренда имеет вид:
![]()
Вычисляем статистику Дарбина – Уотсона для остатков по модели линейного тренда:
DW = ![]() = 1,843115542
= 1,843115542
Из таблицы значений констант Дарбина – Уотсона dU и dL на 5% уровне значимости с двумя влияющими факторами при Т = 48 находим dL = 1,46; dU = 1,63.
Вывод: Так как DW = 1,843115542 > 1,63 = dU и DW = 1,843115542 < 4 – 1,63 = 2,37 = 4 – dU, то делаем вывод об отсутствии в ряде Ut автокорреляции.
Заключение: Модель линейного тренда позволяет избавиться от автокорреляции ряда Ut.
Похожие работы
... Федерации в 1996 году издано Методические рекомендации по планированию, учету и калькулированию себестоимости продукции (работ, услуг) в сельском хозяйстве. [13, с.124] Методические рекомендации призваны обеспечить единство состава и классификации затрат, методов их учета, исчисления себестоимости продукции во всех сельскохозяйственных организациях. Но указанные Методические рекомендации, по ...
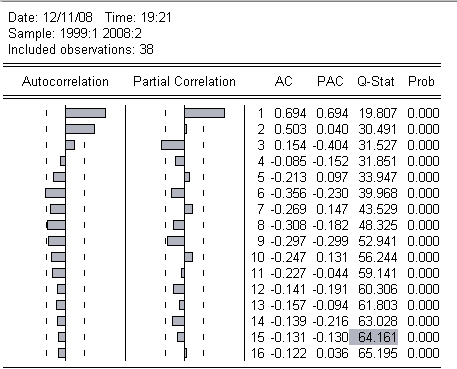
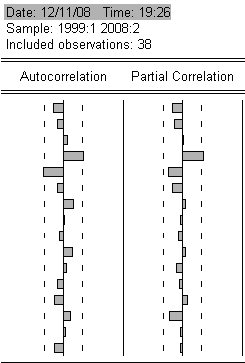
... no cross terms наблюдаемое значение оказывается меньше критического при уровнях значимости ,01 и ,005, из чего следует вывод об отсутствии гетероскедастичности в построенной модели. Проблему автокорреляции исследуем далее при помощи теста Бреуша-Годфри и Q-статистики Бокса-Льюнга. Результаты этих тестов представлены ниже: Breusch-Godfrey Serial Correlation LM Test: F-statistic 33.14949 ...
... оказывает определенное влияние на качество модели, однако ее устранение не является обязательным этапом, поэтому перейдем к дальнейшему исследованию качества регрессионной модели. 2. Исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка Переходим непосредственно к основной теме курсвой - проверяем модель на наличие гетероскедастичности. Для этого ...
... М.М. Анализ временных рядов и прогнозирование. М.: Финансы и статистика, 2001. 5. Джонстон Дж. Эконометрические методы. М.: Статистика, 1980. 6. Образцова О.Н., Назарова О.В., Канторович Г.Г. Экономическая статистика. Эконометрика. Методические материалы. – М.: ГУ – ВШЭ, 2000. 7. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2001. – 543 с. ...
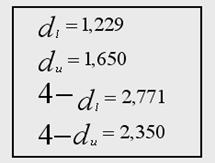
0 комментариев