Навигация
4 вопрос
Теория оценки качества эконометрической модели заключается в четырех леммах (свойствах) регрессионных моделей, построенных с использованием МНК.
Лемма 1. (лемма об отсутствии смещения оцененных остатков)
![]()
Доказательство:
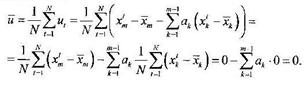
Лемма 2. (лемма о независимости факторов и оцененных остатков):
![]() , если j < m
, если j < m
Доказательство:
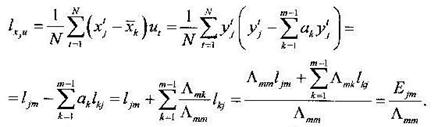
По правилам перемножения матриц ![]() в линейной алгебре величина
в линейной алгебре величина ![]() равна нулю, если j ≠ m.
равна нулю, если j ≠ m.
Лемма 3. (лемма о разложении дисперсии зависимой переменной):
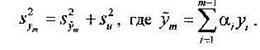
Доказательство:

Далее, из леммы 2 следует, что ![]()
Лемма 4. (лемма о ковариации зависимой переменной и оцененных остатков)
![]()
Доказательство:
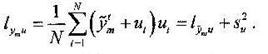

Далее, по лемме 2,
Следовательно, ![]() .
.
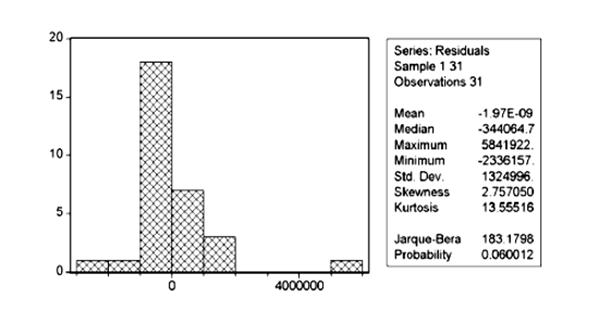
Так же для оценки качества построенной регрессионной зависимости часто используется коэффициент детерминации  , который представляет собой объясненную долю дисперсии модели.
, который представляет собой объясненную долю дисперсии модели.
0 < 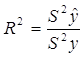 < 1.
< 1.
Чем ближе коэффициент детерминации к единице, тем лучше считается построенная регрессионная зависимость.
![]() в моей работе = 0,680976589.
в моей работе = 0,680976589.
5 вопрос
Методика вычисления доверительного интервала для коэффициента множественной регрессии.
Шаг 1. Вычисляются коэффициенты f и g первой вспомогательной зависимости ![]() , которая строится по следующей логической модели: зависимая переменная – Х, факторы – Y; Z.
, которая строится по следующей логической модели: зависимая переменная – Х, факторы – Y; Z.
Строится ковариационная матрица L [Y; Z; X].
| YY | YZ | YX |
| ZY | ZZ | ZX |
| XY | XZ | XX |
По ней вычисляется обратная матрица, со стандартным обозначением элементов. В соответствии с заданной схемой построения ковариационной матрицы зависимой переменной является третий столбец (в порядке использования при вычислении ковариационной матрицы), следовательно, коэффициенты f и g вычисляются по третьей строке обратной матрицы:
f = -Л31/Л33 g = -Л32/Л33
Шаг 2. Вычисление оцененного ряда и остатков первой вспомогательной модели. Оцененный ряд вычисляется по формуле: ![]() , остатки – по формуле:
, остатки – по формуле: ![]()
Шаг 3. Вычисление коэффициентов m; n второй вспомогательной зависимости ![]() , которая строится по следующей логической модели: зависимая переменная – W, факторы – Y; Z.
, которая строится по следующей логической модели: зависимая переменная – W, факторы – Y; Z.
Строится ковариационная матрица L [Y; Z; W], при вычислении элементов которой аргументы функции КОВАР задаются по следующей схеме:
| YY | YZ | YW |
| ZY | ZZ | ZW |
| WY | WZ | WW |
По ней вычисляется обратная матрица со стандартным обозначением элементов. В соответствии с заданной схемой построения ковариационной матрицы зависимой переменной рассматриваемой логической модели является третий столбец (в порядке использования при вычислении ковариационной матрицы), следовательно, коэффициенты m; n вычисляются по третьей строке обратной матрицы.
m = -Л31/Л33 n = -Л32/Л33
Шаг 4. Вычисление оцененного ряда и остатков второй вспомогательной модели. Оцененный ряд вычисляется по формуле: ![]() , остатки - по формуле:
, остатки - по формуле: ![]() .
.
Шаг 5. Вычисление t – статистики по остаткам вспомогательных зависимостей и границы критической области ![]() (0,05; Т – 2)
(0,05; Т – 2)
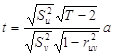
После вычисляем границу критической области с помощью функции Стьюдента.
Шаг 6. Построение доверительного интервала [d1; d2] по формулам:
d1 = 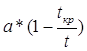 ; d2 =
; d2 = 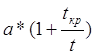
Далее следует вывод, в котором оценивается зависимость ряда w от ряда х и признается либо значительной, либо незначительной.
В моей работе требовалось использовать данную методику для построения трех доверительных интервалов: для коэффициента a, для коэффициента b, и для коэффициента с.
Для коэффициента a:
| Остатки Ut для коэффициента а | Остатки Vt для коэффициента а |
| 0,01149 | -373,36131 |
| -0,06013 | -313,88489 |
| -0,09823 | -500,65379 |
| -0,08774 | -140,33282 |
| -0,02043 | -174,70249 |
| -0,02657 | -201,65287 |
| -0,13940 | -49,72967 |
| -0,05933 | -78,73631 |
| -0,06845 | -83,73499 |
| -0,05766 | 302,64743 |
| -0,06447 | 17,18988 |
| 0,02664 | 731,55961 |
| 0,12052 | -221,19665 |
| 0,04820 | -329,98551 |
| 0,12914 | 143,16744 |
| 0,12048 | 40,82041 |
| 0,13511 | 424,17334 |
| 0,09884 | -95,33570 |
| -0,00916 | -238,17639 |
| -0,01648 | 280,53353 |
| -0,12722 | -25,59792 |
| -0,01471 | 666,76066 |
| -0,00616 | 865,03808 |
| 0,02108 | -90,69097 |
| 0,06339 | -772,54325 |
| -0,00533 | 850,02447 |
| 0,05195 | 631,80160 |
| -0,00201 | 1238,44989 |
| 0,05056 | 32,35612 |
| -0,03110 | -406,36945 |
| -0,02473 | 91,30160 |
| 0,01528 | -300,96111 |
| 0,07173 | -1169,88938 |
| 0,10176 | -808,09808 |
| 0,07283 | -200,25117 |
| -0,00670 | 823,88454 |
| 0,10308 | -623,54830 |
| 0,06409 | -648,32138 |
| -0,08003 | 503,84878 |
| -0,00840 | -8,84112 |
| 0,03691 | 488,12670 |
| -0,07376 | -1566,35279 |
| -0,06725 | -298,82295 |
| -0,09803 | -1004,13310 |
| -0,06623 | 1305,43489 |
| -0,04350 | 2136,17145 |
| -0,04377 | -382,44987 |
| 0,06391 | -464,93619 |
Для коэффициента b:
| Остатки Ut для коэффициента b | Остатки Vt для коэффициента b |
| -23,47559 | -431,84736 |
| 26,95313 | -280,81400 |
| 80,74856 | -342,09514 |
| 22,15600 | -140,96409 |
| -9,90273 | -217,72764 |
| -11,55513 | -253,84115 |
| 30,52604 | -64,03657 |
| 0,08075 | -121,58258 |
| 3,66611 | -122,99332 |
| -1,19381 | 257,38458 |
| 7,98798 | -6,87496 |
| -27,11122 | 673,72051 |
| -65,41348 | -319,91460 |
| 73,11726 | -86,84057 |
| -63,01018 | 57,55076 |
| -55,37166 | -29,34051 |
| -73,45752 | 313,15071 |
| -63,30661 | -203,79782 |
| -23,63244 | -312,10249 |
| -22,00609 | 205,92063 |
| 162,53294 | 344,73506 |
| -20,78616 | 596,90809 |
| -21,89493 | 798,23264 |
| 42,82658 | 46,53499 |
| -15,18956 | -769,75868 |
| 104,44682 | 1143,49027 |
| -42,46293 | 548,63213 |
| -28,21046 | 1156,68200 |
| -45,13863 | -59,43497 |
| -22,92131 | -494,19868 |
| -25,33372 | 1,22374 |
| -25,53171 | -362,55005 |
| -32,00032 | -1208,91214 |
| -44,59080 | -861,16131 |
| 15,79210 | -102,42111 |
| 71,93404 | 1023,80054 |
| 64,16036 | -366,05602 |
| 63,41561 | -421,26096 |
| 223,53285 | 1082,09466 |
| -10,45185 | -44,69351 |
| -47,13174 | 380,75194 |
| -13,66517 | -1658,80454 |
| -22,95825 | -413,00718 |
| -17,20387 | -1124,27874 |
| -7,67160 | 1235,51087 |
| -24,15877 | 2035,81371 |
| -25,19031 | -485,93811 |
| -61,94858 | -594,88904 |
Для коэффициента с:
| Остатки Ut для коэффициента с | Остатки Vt для коэффициента с |
| -161,75633 | -996,28985 |
| -49,68961 | -551,46315 |
| -5,33501 | -592,78957 |
| 13,53108 | -151,23091 |
| -96,20156 | -564,97419 |
| -79,81521 | -532,43409 |
| 117,65294 | 308,21632 |
| -17,21113 | -188,98085 |
| 5,48894 | -112,00876 |
| -7,56409 | 231,26339 |
| 1,76847 | -22,71336 |
| -152,57175 | 155,47175 |
| -308,61077 | -1338,08505 |
| -246,85626 | -1258,37446 |
| -317,64491 | -1002,71812 |
| -296,93056 | -1030,51453 |
| -309,02026 | -683,71813 |
| -237,77974 | -951,53990 |
| -41,76454 | -407,81682 |
| -21,16191 | 185,98051 |
| 89,27625 | 230,44919 |
| -10,92489 | 613,44624 |
| -18,72071 | 787,50315 |
| -109,51511 | -502,77830 |
| -141,29142 | -1277,92309 |
| -74,91716 | 553,77971 |
| -85,87313 | 334,38535 |
| 24,13273 | 1331,17188 |
| -55,28190 | -146,67885 |
| 107,15555 | -10,75987 |
| 111,60315 | 508,88745 |
| 41,30287 | -128,67759 |
| -54,17733 | -1329,24725 |
| -87,13975 | -1074,29363 |
| -60,81987 | -384,73432 |
| 68,41568 | 1086,01965 |
| -134,92937 | -1075,28411 |
| -42,07840 | -766,00742 |
| 162,38522 | 1079,47115 |
| 182,77542 | 698,36254 |
| 126,35774 | 1008,05139 |
| 330,39252 | -330,50831 |
| 336,50046 | 965,58139 |
| 399,40754 | 483,43041 |
| 337,66108 | 2575,11109 |
| 314,02384 | 3330,10235 |
| 323,56685 | 848,52978 |
| 132,18434 | 97,32975 |
Коэффициенты
a = – 726,022045
b = 2,846786592
с = 3,902613829
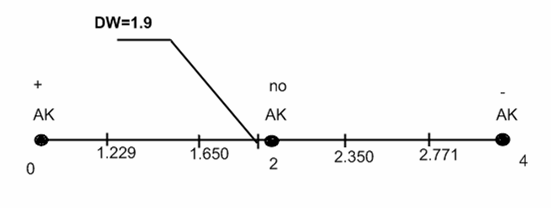
Доверительный интервал [d1; d2] для коэффициента а будет находиться в границах: [-3484,837463; 2032,793373].
Вывод: так как точка 0 принадлежит данному интервалу, то по критерию Стьюдента на уровне значимости 0,05 зависимость ряда w от ряда х признается незначимой.
Доверительный интервал [d1; d2] для коэффициента b будет находиться в границах: [-0,525333618; 6,218906803].
Вывод: так как точка 0 принадлежит данному интервалу, то по критерию Стьюдента на уровне значимости 0,05 зависимость ряда w от ряда х признается незначимой.
Доверительный интервал [d1; d2] для коэффициента с будет находиться в границах: [2,802620379; 5,002607279].
Вывод: так как точка 0 не принадлежит данному интервалу, то по критерию Стьюдента на уровне значимости 0,05 зависимость ряда w от ряда х признается значимой и положительной.
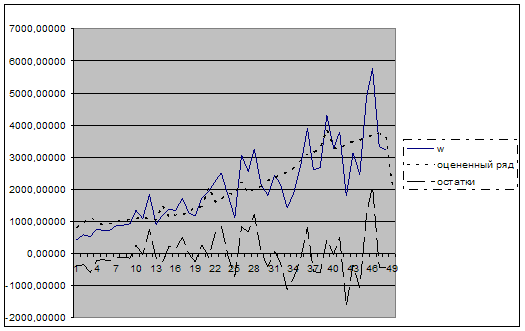
6 вопрос
По данным моего исследования я построила график зависимой переменной w, оцененного ряда ![]() и остатков
и остатков ![]() .
.
Похожие работы
... Федерации в 1996 году издано Методические рекомендации по планированию, учету и калькулированию себестоимости продукции (работ, услуг) в сельском хозяйстве. [13, с.124] Методические рекомендации призваны обеспечить единство состава и классификации затрат, методов их учета, исчисления себестоимости продукции во всех сельскохозяйственных организациях. Но указанные Методические рекомендации, по ...
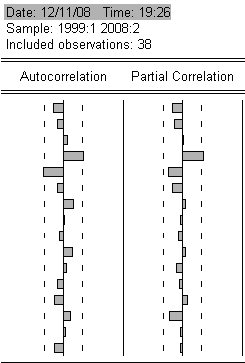
... no cross terms наблюдаемое значение оказывается меньше критического при уровнях значимости ,01 и ,005, из чего следует вывод об отсутствии гетероскедастичности в построенной модели. Проблему автокорреляции исследуем далее при помощи теста Бреуша-Годфри и Q-статистики Бокса-Льюнга. Результаты этих тестов представлены ниже: Breusch-Godfrey Serial Correlation LM Test: F-statistic 33.14949 ...
... оказывает определенное влияние на качество модели, однако ее устранение не является обязательным этапом, поэтому перейдем к дальнейшему исследованию качества регрессионной модели. 2. Исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка Переходим непосредственно к основной теме курсвой - проверяем модель на наличие гетероскедастичности. Для этого ...
... М.М. Анализ временных рядов и прогнозирование. М.: Финансы и статистика, 2001. 5. Джонстон Дж. Эконометрические методы. М.: Статистика, 1980. 6. Образцова О.Н., Назарова О.В., Канторович Г.Г. Экономическая статистика. Эконометрика. Методические материалы. – М.: ГУ – ВШЭ, 2000. 7. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2001. – 543 с. ...
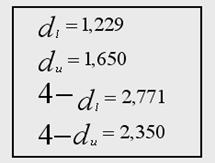
0 комментариев