Навигация
Выбор и расчет посадок для гладких соединений c расчетом размерной цепи
Содержание
Введение
1. Вопрос по стандартизации
2.Выбор и расчет посадок для гладких соединений
2.1 Выбор посадок по аналогии
2.2 Расчет и выбор посадки с натягом
2.3 Выбор средств измерения
3.Взаимозаменяемость стандартных соединений
3.1 Выбор и расчет посадок колец подшипников качения
3.2 Выбор и расчет посадок шпоночных соединений
3.3 Выбор и расчет посадок шлицевых соединений
3.4 Взаимозаменяемость резьбовых соединений
4.Расчет размерной цепи
4.1 Расчет методом максимум – минимум
4.2 Расчет вероятностным методом
Список литературы
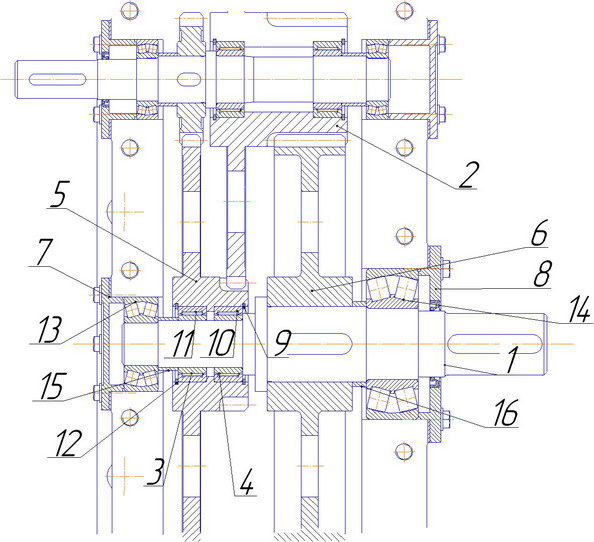
Приложение А (обязательное. Сборочный чертеж – мост приводной).
Приложение Б (обязательное. Чертеж – кожух полуоси).
Введение
На современном этапе развития науки и техники стандартизация глубоко проникла во все области жизни, как на производстве, так и в быту. Стандартизация основывается на современных техники и практического опыта и определяет основу не только настоящего, но и будущего развития и должна осуществляться неразрывно с процессом.
Основные назначения стандартов – нормативно-техническое обеспечение мероприятий по научно-техническому и торгово-экономическому сотрудничеству, дальнейшему развитию экономической интеграции.
Необходимость расширения масштабов работ по стандартизации вызывается, в частными, увеличением поставок специализированной машиностроительной продукции. Специализация производства как в пределах одной страны, так и в пределах региона требует проведения работ по стандартизации в области взаимозаменяемости деталей, сборочных единиц и агрегатов; и в частности применения и совершенствования единой системы стандартов на допуски и насадки.
Разработанная система допусков и насадок включает множество стандартов, в том числе, на допуски и насадки гладких соединений, допуски резьб и зубчатых передач, шпоночных и шлицевых соединений. Так как эти соединения преобладают, указанные стандарты являются базой для разработки других стандартов в области взаимозаменяемости. Поэтому подготовка современного инженера включает освоение широкого круга вопросов, связанных со стандартизацией.
Курс "метрология, стандартизация, квалиметрия" является логическим завершением цикла общетехнических курсов теорий машин и механизмов, технологии материалов, сопротивление материалов, деталей машин. Если другие курсы являются теоретической основой проектирования машин и механизмов, то данный курс рассматривает вопросы обеспечения точности
геометрических параметров, как необходимое условие взаимозаменяемости и таких важнейших показателей качества, как надежность долговечности. Полученные при изучении курса знания закрепляются в ходе изучения специальных дисциплин, в процессе курсового и дипломного проектирования.
1. Вопрос по стандартизации
Каждый вид продукции характеризуется параметрами, количественно выраженными конкретными числами. Например: автомобиль грузоподъемностью 8 т, электродвигатель мощностью 100 к Вт, вал диаметром 50 мм. Значения параметра определяется или путем расчетов, или назначаются из конструктивных соображений. При этом числовые характеристики параметров могут принимать самые разные значения. Без ограничения применяемых числовых характеристик унификация и стандартизация параметров были бы невозможны. Кроме того, опыт стандартизации показал, что последовательности чисел, характеризующих параметры стандартизуемых объектов, не должны быть случайными, а должны представлять собой ряды, образованные по математическим законам. Это позволит увязать между собой как геометрические размеры, так и параметры, характеризующие мощность, производительность, грузоподъемность, прочность.
Задача эта решается установлением рядов предпочтительных чисел при выборе числовых значений параметров в расчетах, проектировании, составлении различных технических документов. Система предпочтительных чисел является теоретической базой и основой стандартизации. Применение предпочтительных чисел позволяет унифицировать размеры и параметры продукции в масштабах всего народного хозяйства страны и международном масштабе. О важности взаимосвязи параметров отдельных видов продукции свидетельствует пример организации странами – членами СЭВ контейнерных перевозок водным, железнодорожным и автомобильным транспортом, при которых указаны параметры контейнеров, судов, железнодорожных платформ, автомобильных кузовов, подъемно – транспортных устройств в местах перегрузок контейнеров.
Ряды предпочтительных чисел должны отвечать следующим требованиям: быть бесконечными как в сторону малых, так и в сторону больших размеров, включать единицу и все десятикратные значения любого члена, быть простыми и легко запоминаемыми.
В начальный период стандартизации получили распространения ряды, выраженные арифметическими прогрессиями, но существенным недостатком арифметической прогрессии является ее относительная неравномерность. При постоянной абсолютной разности относительная разность между членами арифметического ряда 1, 2, 3,…10 для чисел 1 и 2 составляет 200%, а для чисел 9 и 10 всего 11%.
В связи с этим позднее стали применять ступенчато – арифметические ряды, например, ряды стандартных резьб:
1 – 1,1 – 1,2 – 1,4 – 1,6 – 1,8 – 2,0 – 2,2 – 2,5 – 3,0 – 3,5 – 4,0 – 4,5 - … - 145 – 150 – 155 - 160 – 165 - …ё1
у которых разности возрастают с увеличением абсолютного размера и соответственно равны 0,1; 0,2; 0,5; 5.
Тем не менее применение арифметической прогрессии в большинстве случаев не целесообразно и поэтому находят ограниченное распространение.
В большей степени удовлетворяют требованиям стандартизации геометрические прогрессии, у которых относительная разность между любыми слитными числами ряда является постоянной. Геометрическая прогрессия характеризуется тем, что отношение двух смежных членов всегда постоянна и равно знаменателю прогрессии
1 – 2 – 4 – 8 – 16 – 32 - …
1 – 1,25 – 1,6 – 2,0 – 2,5 – 3,15 – 4 - …
1 – 10 – 100 – 1000 – 10000 - …
В приведенных ряжах знаменатели соответственно равны 2; 1,25; 10.
Геометрические прогрессии обладают рядом ценных свойств, которые дают основание использовать их для построения рядов предпочтительных чисел.
В геометрической прогрессии, имеющей в числе членов единицу каждый ее член (Ni) определяется из выражения.
Ni =φ![]()
Где I – порядковый номер члена
φ - знаменатель прогрессии.
Для приведенного выше ряда
N![]() =2
=2![]() =16
=16
Необходимо иметь в виду, что порядковый номер единицы во всех рядах равно
N![]() =2
=2![]() =1
=1
В первые свойства геометрической прогрессии были использованы в 1877 – 1879 гг. офицером французского инженерного корпуса Ф. Ренаром при разработке системы характеристик хлопчатобумажных канатов, которые изготавливались бы заранее независимо от места применения. За основу был взят канат, один метр которого имел массу аm. Знаменатель прогрессии был выбран с таким расчетом, чтобы каждый пятый член ряда давал десятикратное увеличение, то есть
аφ![]() =10а, откуда φ = 10
=10а, откуда φ = 10![]()
Числовой ряд выглядел следующим образом:
а; а![]() ; а(
; а(![]() )
)![]() ; а (
; а (![]() )
)![]() ; а(
; а(![]() )
)![]() ; а(
; а(![]() )
)![]() .
.
После вычисления:
а; 1,5849а; 2,5119а; 3,9811а; 6,3096а; 10а.
После округления:
1; 1,6; 2,5; 4; 6,3; 10.
Из этого ряд, условно обозначенного как ряд R5, были впоследствии образованы ряды R10, R20, R40; имеющие соответственно знаменатели:![]() ;
;![]() ;
;![]()
Не всегда имеется необходимость использовать все числа того или иного ряда. Стандартом допускается применять производные ряды, получаемые из основных или дополнительного путем отбора каждого второго, третьего, четвертого или n – го члена ряда.
Частота ряда в каждом конкретном случае должна быть основана технически и экономически. Сужение ряда ведет к увеличению серийности, а следовательно снижению трудоемкости и себестоимости, но может вызывать излишние затраты при эксплуатации.
Похожие работы
... : TN=TD+Td TN=54+20=74мкм KT=(TN+Nз.с.)/TN KT=(65,2+0,85)/40=1,6>1 Следовательно, посадка выбрана точно. Вычерчиваем схему расположения полей допусков и эскизы соединения и его деталей с нанесением соответствующих размеров и обозначений. 3. Расчет и выбор посадок подшипников качения 1. Для подшипникового узла (тихоходный вал) выбрать и обосновать класс точности подшипника ...
... ) Nзе=Nminf-Nmin Nзе=16.05-7=9.03 мкм Определяем коэффициент запаса точности выбранной посадки: TN= Nmax-Nmin TN=83-7=76 Рекомендуется значение К=1…2.Следовательно, посадка выбрана точно. 3. РАСЧЕТ И ВЫБОР ПОСАДОК ПОДШИПНИКОВ КАЧЕНИЯ Для подшипникового узла быстроходного вала выбрать и обосновать класс точности подшипника качения. Установить вид нагружения внутреннего и ...
... Изм. Лист № документа Подпись Дата 2.3. Расчет характеристик посадок подшипника. Подшипниковый узел ведущего вала. К данному узлу шпиндельной головки не предъявлено особых требований к точности, следовательно, выбираем шариковый радиальный однорядный подшипник нулевого класса точности 303. ГОСТ 8338-75 Внутренний диаметр d = ...
... привертных крышек поз. 7, 8, которые фиксируют наружные кольца опорных подшипников.. На хвостовик вала устанавливается шпонка и надевается зубчатая муфта. Рисунок 1.1 - Сборочная единица (Тихоходный вал редуктора) 2. ИСХОДНЫЕ ДАННЫЕ Тип производства – массовое. Передаваемый крутящий момент – 1,8 · 10 6 Н · мм. Частота вращения вала n =66 об/мин. Параметры зубчатого колеса: m n = 6 мм; ...

0 комментариев