Возведение обеих частей уравнения в квадрат
Стандартные иррациональные уравнения
Иррациональные уравнения, которые решаются введением новой переменной
Применение основных свойств функции
Использование ограниченности функции
Использование наибольшего и наименьшего значений функции
Иррациональные показательные уравнения
Навигация
Стандартные иррациональные уравнения
Иррациональные уравнения
36308
знаков
0
таблиц
4
изображения
2. Стандартные иррациональные уравнения
Как правило, в школьном курсе рассмотрение иррациональных уравнений сводится к разбору нескольких несложных примеров. Они в большинстве случаев решаются возведением в квадрат левой и правой частей уравнения. После решения обязательно выполняется проверка. Не обращается внимание на то, что иррациональные уравнения могут решаться и с использованием понятия равносильности. В данном параграфе представлены различные виды иррациональных уравнений, которые можно отнести к стандартным и решать одним из следующих методов, а именно:
1) метод перехода к уравнению - следствию с последующей проверкой полученных корней;
2) метод равносильного перехода к уравнению или к смешанной системе;
3) метод введения новой переменной.
2.1 Уравнения вида 
Пример 1. Решить уравнение 
.
Решение. Возведем обе части исходного уравнения в квадрат.
.
О т в е т: {6}.
Пример 2. Решить уравнение 
.
Решение. В левой части исходного уравнения стоит арифметический квадратный корень – он по определению неотрицателен, а в правой части – отрицательное число.
Следовательно, уравнение не имеет корней.
О т в е т:
.
Запишем равносильность, с помощью которой решаются уравнения данного вида.
, если 
и не имеет решения, если 
.
Пример 3. Решить уравнение 
.
Решение. Возведем обе части исходного уравнения в куб.
; 
.
О т в е т: {-5}.
Запишем равносильность, с помощью которой решаются уравнения данного вида: 
.
2.2 Уравнения вида 
Довольно часто при решении уравнений данного вида учащиеся используют следующую формулировку свойства произведения «Произведение двух сомножителей равно нулю, когда хотя бы один из них равен нулю». Заметим, что формулировку свойства произведения должна выглядеть следующим образом: « произведение двух сомножителей равно нулю, когда хотя бы один из них равен нулю, а другой при этом имеет смысл».
Запишем равносильность, с помощью которой решаются уравнения данного вида:
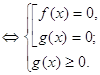
Пример 1. Решить уравнение 
.
Решение.
.
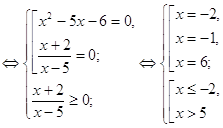О т в е т: {-2;6}.
Пример 2. Решить уравнение 
.
Решение. В данном случае уравнение не имеет вида, указанного в заголовке. Следовательно, его необходимо преобразовать. Но сначала найдем ОДЗ переменной 
.
ОДЗ: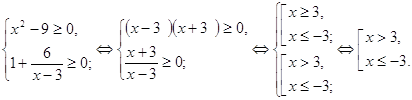
Преобразуем уравнение к виду 
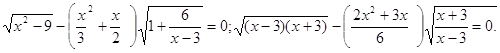
При решении уравнения учащиеся часто необоснованно делят обе части уравнения на выражение, содержащее неизвестное (в данном случае, на 
), что приводит к потере корня и приобретению «постороннего». Подобные уравнения, содержащие в обеих частях общий множитель, следует решать переносом всех членов в одну часть и разложением полученного выражения на множители.
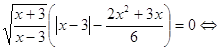
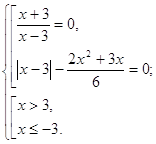
Решим каждое уравнение из совокупности.
; 
.
(1).
Учитывая, что ОДЗ: 
получаем, что уравнение (1) равносильно совокупности: 
. Тогда 
, 
не удовлетворяет условию 
, данное уравнение не имеет корней.
Следовательно, совокупность примет следующий вид: 
Вернемся к системе: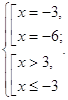 
О т в е т: {-3;6}.
Похожие работы
... введение нового(новых) неизвестного. Пример 2. Обозначим , тогда а) Уравнение примет вид: Корень не удовлетворяет условию Ответ: 76. Методы решения иррациональных уравнений. Методы решения иррациональных уравнений, как правило основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному, либо ...
... , т.к. . б) , т.к. . в) . Выясним, при каких n выражения под знаком модуля меняют знак: n=-1, n=1, n=0. 1) Если n<-1, то 2) Если -1£n<0, то 3) Если 0<n<1, то 4) Если n³1, то Ответ: II. Иррациональные уравнения. Рассмотрим уравнение вида . Основной метод решения – возведение обеих частей уравнения в степень n. При этом, если n – четное, то могут возникнуть ...
... по способам решения иррациональных неравенств вида , рассмотрена подробно, изложение теории строгое. Только в учебнике Виленкина рассматривается решение иррационального неравенства вида . Наиболее большой объем упражнений для решения иррациональных уравнений и неравенств представлен в учебниках [11] и [5]. В учебнике [4] упражнений не много, но они разнообразны. Основные понятия, относящиеся к ...
... литературы дается характеристика этих форм, разработана методика применения самостоятельной работы вместе с иными формами организации познавательной деятельности на факультативных занятиях в выпускных классах средней школы, изучены учебные возможности учащихся в экспериментальной группе, проведена опытно- экспериментальная работа по включению самостоятельной работы школьников в процесс обучения. ...
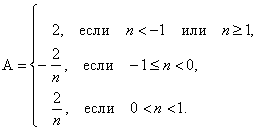
0 комментариев