Навигация
Использование наибольшего и наименьшего значений функции
3.2.2 Использование наибольшего и наименьшего значений функции
Справедливы следующие утверждения:
1) наибольшее (наименьшее) значение непрерывной функции, принимаемое на интервале ![]()
![]() может достигаться в тех точках интервала
может достигаться в тех точках интервала ![]() , в которых ее производная равна нулю или не существует (каждая такая точка называется критической точкой);
, в которых ее производная равна нулю или не существует (каждая такая точка называется критической точкой);
2) чтобы найти наибольшее и наименьшее значение непрерывной на отрезке![]() функции, имеющей на интервале (а;b) конечное число критических точек, достаточно вычислить значения функции во всех критических точках, принадлежащих интервалу (а;b), а также в концах отрезка и из полученных чисел выбрать наибольшее и наименьшее;
функции, имеющей на интервале (а;b) конечное число критических точек, достаточно вычислить значения функции во всех критических точках, принадлежащих интервалу (а;b), а также в концах отрезка и из полученных чисел выбрать наибольшее и наименьшее;
3) если в критической точке ![]() функция непрерывна, а ее производная, проходя через эту точку, меняет знак с «минуса» на «плюс», то точка
функция непрерывна, а ее производная, проходя через эту точку, меняет знак с «минуса» на «плюс», то точка ![]() - точка минимума, а если ее производная меняет знак с «плюса» на «минус», то
- точка минимума, а если ее производная меняет знак с «плюса» на «минус», то ![]() - точка максимума.
- точка максимума.
Пример 1. Решить уравнение ![]() .
.
Решение. Найдем ОДЗ переменной x.
ОДЗ: ![]() .
.
Рассмотрим непрерывную функцию ![]() на отрезке [2;4], где D(f)=[2;4].
на отрезке [2;4], где D(f)=[2;4].
Функция f(x) на интервале (2;4) имеет производную:![]() , обращаются в ноль только при х=3.
, обращаются в ноль только при х=3.
Т.к. функция f(x)непрерывна на отрезке [2;4], то ее наибольшее и наименьшее значения находятся среди чисел f(3);f(2);f(4). Т.к. f(3)=2;f(2)=f(4)=![]() ,
, ![]() , то наибольшее значение f(x) есть f(3)=2.
, то наибольшее значение f(x) есть f(3)=2.
Следовательно, данное уравнение имеет единственный корень: 3.
О т в е т:{3}.
4. Смешанные иррациональные уравнения и методы их решения
4.1 Иррациональные уравнения, содержащие двойную иррациональность
Пример 1. Решить уравнение ![]()
Решение. Возведем обе части уравнения в куб.
![]() Возведем обе части полученного уравнения в квадрат.
Возведем обе части полученного уравнения в квадрат. ![]()
Введем новую переменную. Пусть ![]() , тогда
, тогда ![]() . Получаем, что
. Получаем, что ![]() . Тогда
. Тогда ![]() .
.
Выполним обратную замену. ![]() Или
Или ![]() .
.
Тогда ![]() или
или ![]()
Проверка показывает, что ![]() не является корнем данного уравнения, а 1- является.
не является корнем данного уравнения, а 1- является.
О т в е т: {1}.
Пример 2. Решить уравнение ![]()
Решение.
![]()
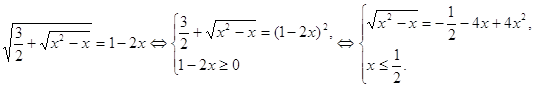
Введем новую переменную. Пусть ![]() . Тогда
. Тогда ![]()
Тогда система примет следующий вид:
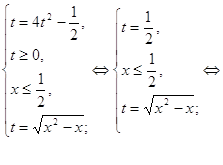
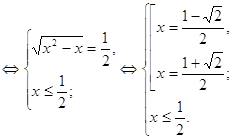
О т в е т: 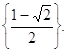
Пример 3. Решить уравнение ![]()
Решение. Введем новую переменную. Пусть ![]() . Тогда
. Тогда ![]() . Получаем, что
. Получаем, что
![]()
![]() .
.
Т.к. ![]() , то данное уравнение равносильно следующему:
, то данное уравнение равносильно следующему: ![]()
Получаем, что ![]() . Учитывая, что
. Учитывая, что ![]() , то решения:
, то решения: ![]() . Следовательно,
. Следовательно, ![]() .
.
Выполним обратную замену. ![]() . Тогда
. Тогда ![]()
О т в е т: [-4;0].
Пример 4. Решить уравнение ![]()
Решение. Преобразуем подкоренные выражения.
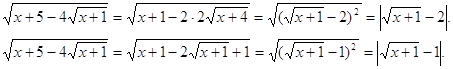
Вернемся к исходному уравнению.
![]()
Последнее уравнение решим методом интервалов.
1. Пусть ![]() . Получаем, что
. Получаем, что
![]() .
.
Т.к. ![]() , то на данном промежутке уравнение не имеет корней.
, то на данном промежутке уравнение не имеет корней.
2. Пусть ![]() . Получаем, что
. Получаем, что ![]() Равенство верно. Найдем все значения
Равенство верно. Найдем все значения ![]() из данного промежутка.
из данного промежутка.![]() . Следовательно,
. Следовательно, ![]()
3. Пусть ![]() . Получаем, что
. Получаем, что ![]() . Т.к.
. Т.к. ![]() , то на данном промежутке уравнение не имеет корней.
, то на данном промежутке уравнение не имеет корней.
Замечание. Данное уравнение можно решать, выполнив замену переменной ![]() . После решения исходного уравнения относительно переменной
. После решения исходного уравнения относительно переменной ![]() , выполнив обратную замену, найдем корень уравнения.
, выполнив обратную замену, найдем корень уравнения.
О т в е т: [0;3].
Замечание. Выражение вида ![]() обычно называют двойным радикалом или сложным радикалом.
обычно называют двойным радикалом или сложным радикалом.
Если подкоренное выражение представляет собой полный квадрат, то можно в двойном радикале освободиться от внешнего радикала, воспользовавшись равенством ![]() .
.
Преобразование двойных радикалов.
Упражнение 1. Освободиться от внешнего радикала в выражении ![]() .
.
Решение. Слагаемое ![]() можно рассматривать как удвоенное произведение чисел
можно рассматривать как удвоенное произведение чисел ![]() и
и ![]() или чисел
или чисел ![]() и
и ![]() . Число 7 должно быть равно сумме квадратов этих чисел. Подбором находим, что это условие выполняется для чисел
. Число 7 должно быть равно сумме квадратов этих чисел. Подбором находим, что это условие выполняется для чисел ![]() и
и ![]() , т.е.
, т.е. ![]() .
.
Получаем, что
![]()
О т в е т:![]() .
.
Похожие работы
... введение нового(новых) неизвестного. Пример 2. Обозначим , тогда а) Уравнение примет вид: Корень не удовлетворяет условию Ответ: 76. Методы решения иррациональных уравнений. Методы решения иррациональных уравнений, как правило основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному, либо ...
... , т.к. . б) , т.к. . в) . Выясним, при каких n выражения под знаком модуля меняют знак: n=-1, n=1, n=0. 1) Если n<-1, то 2) Если -1£n<0, то 3) Если 0<n<1, то 4) Если n³1, то Ответ: II. Иррациональные уравнения. Рассмотрим уравнение вида . Основной метод решения – возведение обеих частей уравнения в степень n. При этом, если n – четное, то могут возникнуть ...
... по способам решения иррациональных неравенств вида , рассмотрена подробно, изложение теории строгое. Только в учебнике Виленкина рассматривается решение иррационального неравенства вида . Наиболее большой объем упражнений для решения иррациональных уравнений и неравенств представлен в учебниках [11] и [5]. В учебнике [4] упражнений не много, но они разнообразны. Основные понятия, относящиеся к ...
... литературы дается характеристика этих форм, разработана методика применения самостоятельной работы вместе с иными формами организации познавательной деятельности на факультативных занятиях в выпускных классах средней школы, изучены учебные возможности учащихся в экспериментальной группе, проведена опытно- экспериментальная работа по включению самостоятельной работы школьников в процесс обучения. ...
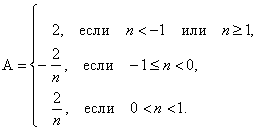


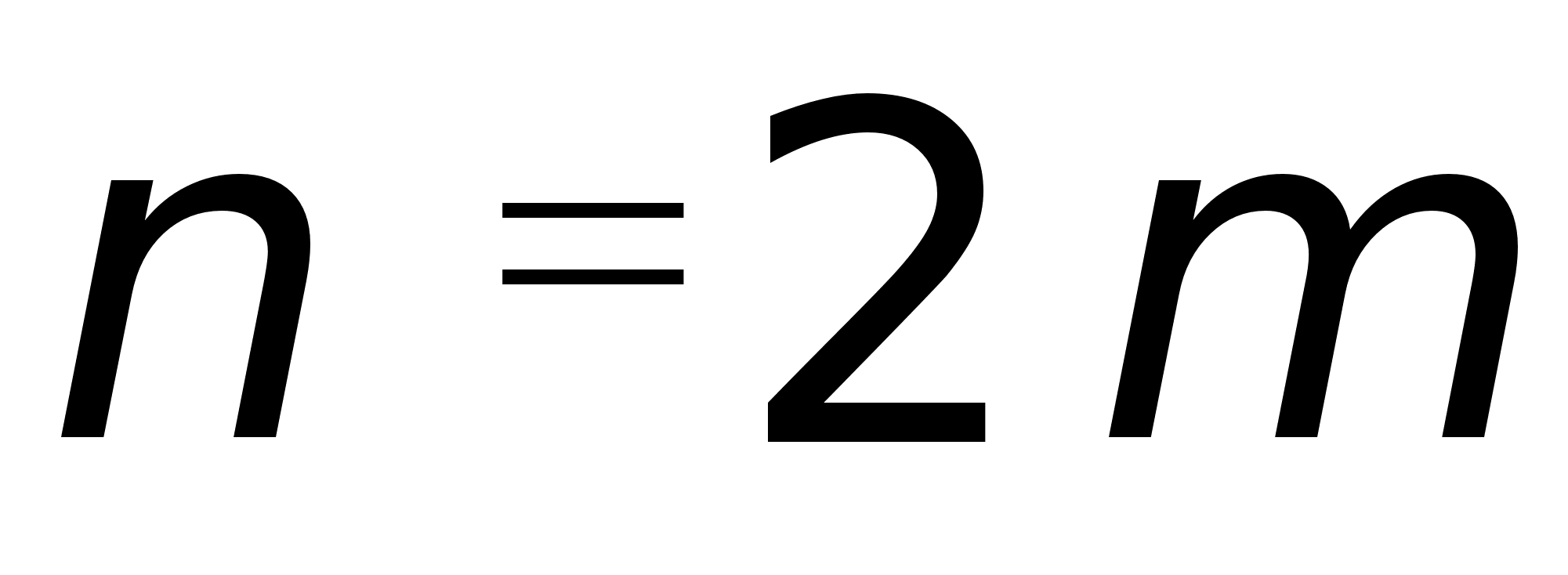
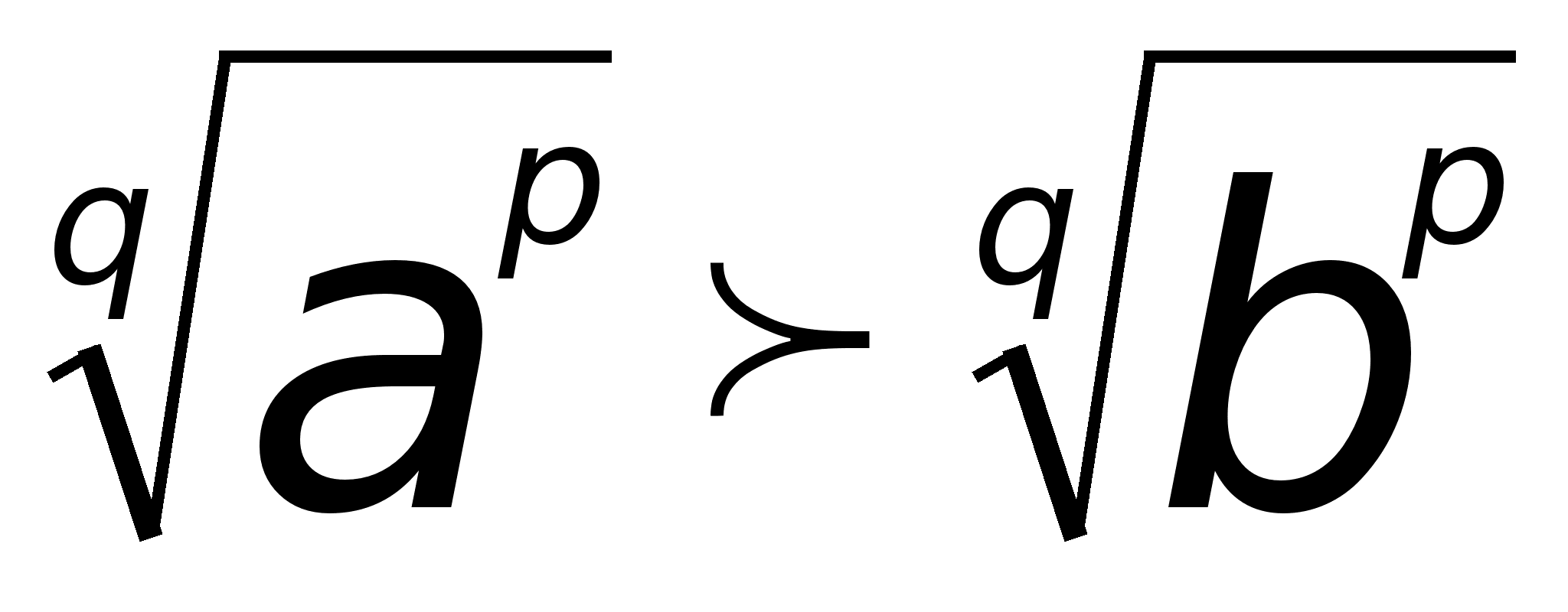
0 комментариев