Навигация
Применение основных свойств функции
3.1 Применение основных свойств функции
3.1.1 Использование области определения уравнения
Иногда знание области определения уравнения позволяет доказать, что уравнение не имеет решений, а иногда позволяет найти решения уравнения непосредственной подстановкой чисел из нее.
Пример 1. Решить уравнение ![]() .
.
![]() Решение. Найдем область определения уравнения.
Решение. Найдем область определения уравнения.
ОДЗ: ![]() .
.
Следовательно, данная система решений не имеет.
Т.к. система решений не имеет, то и данное уравнение не имеет корней.
О т в е т: ![]() .
.
Пример 2. Решить уравнение ![]()
Решение. Найдем ОДЗ переменной х.
ОДЗ: 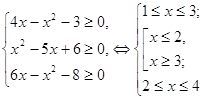 .
.
Следовательно, ![]() или
или ![]() .
.
Таким образом, решения данного уравнения могут находиться среди найденных двух чисел.
Проверкой убеждаемся, что только 2 является корнем исходного уравнения.
О т в е т: {2}.
3.1.2 Использование области значений уравнений
Пример 1. Решить уравнение ![]()
Решение. Т.к. ![]() , следовательно,
, следовательно, ![]() , но
, но ![]() (правая часть уравнения отрицательна, а левая положительна), значит данное уравнение не имеет решений.
(правая часть уравнения отрицательна, а левая положительна), значит данное уравнение не имеет решений.
О т в е т: ![]()
Пример 2. Решить уравнение ![]() .
.
Решение. Т.к. ![]() , то
, то
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Следовательно, левая часть уравнения принимает неотрицательное значение только при ![]() . А это значит, что его корнем может быть только значение 5, а может случиться, что уравнение вообще не будет иметь корней. Для решения этого вопроса выполним проверку.
. А это значит, что его корнем может быть только значение 5, а может случиться, что уравнение вообще не будет иметь корней. Для решения этого вопроса выполним проверку.
Проверка показывает, что 5 является корнем исходного уравнения.
О т в е т: {5}.
3.1.3 Использование монотонности функции
Решение уравнений и неравенств с использованием свойств монотонности основывается на следующих утверждениях.
1. Пусть f(x) - непрерывная и строго монотонная функция на промежутке Q, тогда уравнение f(x)=c, где c - данная константа может иметь не более одного решения на промежутке Q.
2. Пусть f(x) и g(x) - непрерывные на промежутке Q функции, f(x) - строго возрастает, а g(x)- строго убывает на этом промежутке, тогда уравнение f(x)= g(x) может иметь не более одного решения на промежутке Q.
Отметим, что в каждом из случаев промежутки Q могут иметь один из видов: ![]()
Пример 1. Решим уравнение ![]()
Решение. Найдем ОДЗ переменной х.
ОДЗ: ![]() .
.
Следовательно, ![]() .
.
На ОДЗ функции ![]() и
и ![]() непрерывны и строго убывают, следовательно, непрерывна и убывает функция
непрерывны и строго убывают, следовательно, непрерывна и убывает функция ![]() . Поэтому каждое свое значение функция h(x) принимает только в одной точке. Т.к. h(2)=2 , то 2 является единственным корнем исходного уравнения.
. Поэтому каждое свое значение функция h(x) принимает только в одной точке. Т.к. h(2)=2 , то 2 является единственным корнем исходного уравнения.
О т в е т: {2}.
Похожие работы
... введение нового(новых) неизвестного. Пример 2. Обозначим , тогда а) Уравнение примет вид: Корень не удовлетворяет условию Ответ: 76. Методы решения иррациональных уравнений. Методы решения иррациональных уравнений, как правило основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному, либо ...
... , т.к. . б) , т.к. . в) . Выясним, при каких n выражения под знаком модуля меняют знак: n=-1, n=1, n=0. 1) Если n<-1, то 2) Если -1£n<0, то 3) Если 0<n<1, то 4) Если n³1, то Ответ: II. Иррациональные уравнения. Рассмотрим уравнение вида . Основной метод решения – возведение обеих частей уравнения в степень n. При этом, если n – четное, то могут возникнуть ...
... по способам решения иррациональных неравенств вида , рассмотрена подробно, изложение теории строгое. Только в учебнике Виленкина рассматривается решение иррационального неравенства вида . Наиболее большой объем упражнений для решения иррациональных уравнений и неравенств представлен в учебниках [11] и [5]. В учебнике [4] упражнений не много, но они разнообразны. Основные понятия, относящиеся к ...
... литературы дается характеристика этих форм, разработана методика применения самостоятельной работы вместе с иными формами организации познавательной деятельности на факультативных занятиях в выпускных классах средней школы, изучены учебные возможности учащихся в экспериментальной группе, проведена опытно- экспериментальная работа по включению самостоятельной работы школьников в процесс обучения. ...
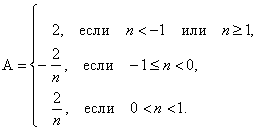


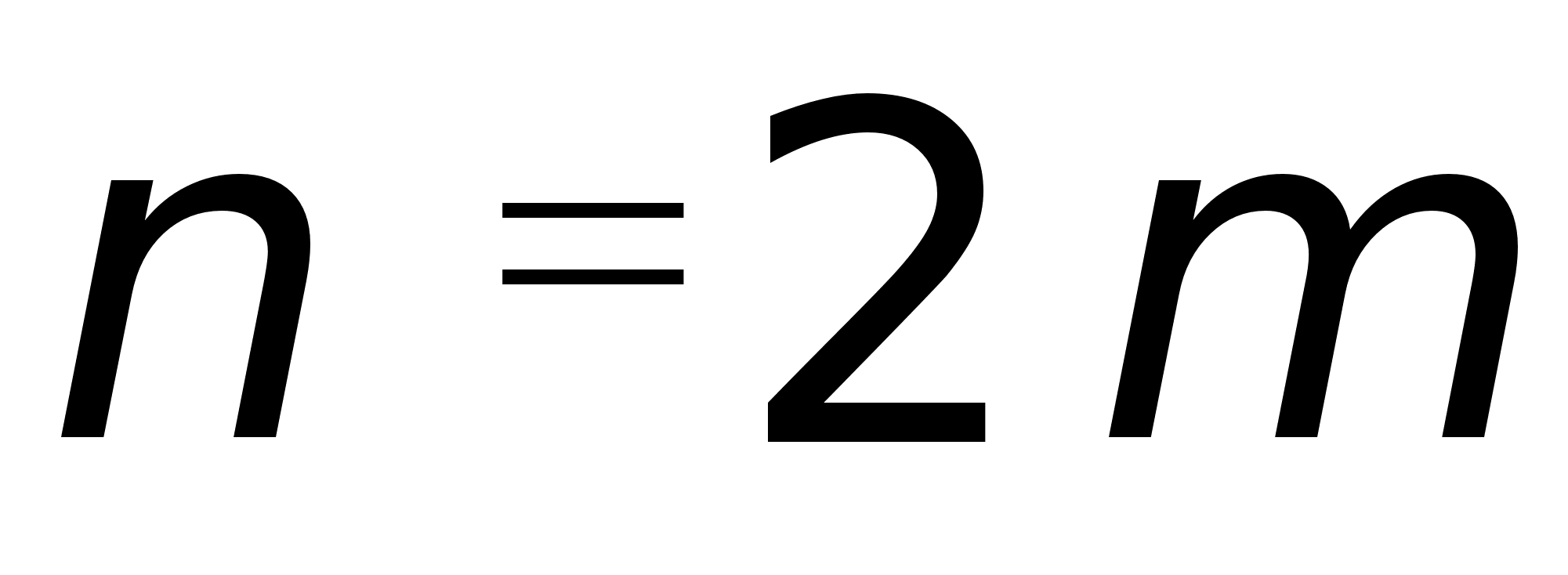
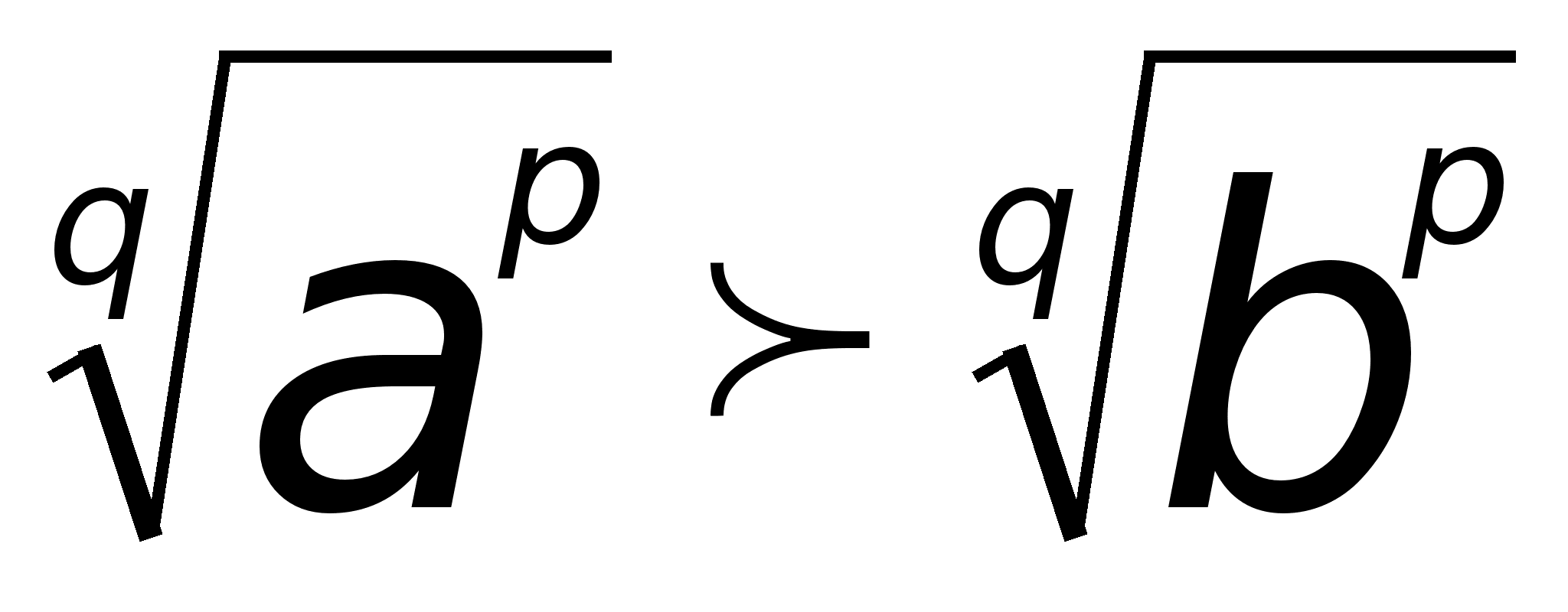
0 комментариев