Возведение обеих частей уравнения в квадрат
Стандартные иррациональные уравнения
Иррациональные уравнения, которые решаются введением новой переменной
Применение основных свойств функции
Использование ограниченности функции
Использование наибольшего и наименьшего значений функции
Иррациональные показательные уравнения
Навигация
Иррациональные показательные уравнения
Иррациональные уравнения
36308
знаков
0
таблиц
4
изображения
4.2. Иррациональные показательные уравнения
Пример 1. Решить уравнение 
.
Решение. ; 
- решений нет.
О т в е т: 
Пример 2. Решить уравнение 
Решение.
- Решений нет, т.к. 
О т в е т:
Пример 3. Решить уравнение 
Решение.
; 
О т в е т: 
.
Приме 4. Решить уравнение 
Решение.
; 
Введем новую переменную. Пусть 
. Получаем, что 
. Тогда 
Выполним обратную замену. 
Или 
;
- решений нет.
;
.
О т в е т:{3}.
Пример 5. Решить уравнение 
Решение. Множество М – общая часть (пересечение) областей существования функций 
- есть все 
На множестве М функции 
и 
положительны. Поэтому, логарифмируя обе части уравнения, получим уравнение, равносильное исходному на М.
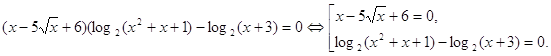
Решим уравнения совокупности.
. Введем новую переменную. Пусть 
. Получаем, что 
. Тогда 
. Выполним обратную замену. 
или 
. Тогда 
или 
.
Получаем, что исходное уравнение равносильно системе:
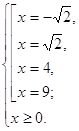
О т в е т: 
.
Замечание. В задачах повышенной сложности встречаются уравнения вида 
, где 
- некоторые положительные числа. Такие уравнения не являются иррациональными уравнениями, т.к. не содержат переменной под знаком радикала, но все, же разберем их решение в данном пункте.
Пример 6. Решить уравнение 
Решение. Преобразуем выражение 
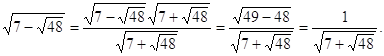
Тогда исходное уравнение примет вид: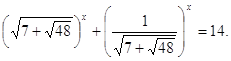 
Замечание. Можно заметить, что 
, следовательно, 
и 
- взаимно обратные числа. Тогда 
. Введем новую переменную. Пусть 
, а 
Получаем, что исходное уравнение равносильно следующему 
. Тогда 
Выполним обратную замену.
или 
; 
;
Тогда 
.
; 
Тогда 
О т в е т :{-2;2}.
4.3 Иррациональные логарифмические уравнения
Пример 1. Решить уравнения 
Решение. 
; 
Учитывая, что 
, данное уравнение равносильно системе:
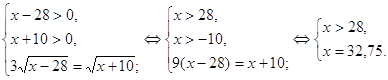
О т в е т:{32,75}.
Пример 2. Решить уравнения 
Решение. 
. Преобразуем правую часть уравнения.
Вернемся к исходному уравнению.
; 
Введем новую переменную. Пусть 
. Получаем, что
.
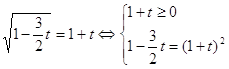Решим уравнение системы.
; 
.
Тогда 
Вернемся к системе: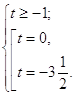 
Следовательно, 
Выполним обратную замену: 
Проверка показывает, что 1 является корнем исходного уравнения.
О т в е т: {1}.
Пример 3. решить уравнение 
Решение. Найдем ОДЗ переменной х.
ОДЗ:
.
На ОДЗ исходное уравнение равносильно уравнению
; 
; 
Введем новую переменную. Пусть 
или 
; 
; 
О т в е т: {3;81}.
Заключение
Данная курсовая работа помогла мне научиться решать иррациональные уравнения следующих типов: стандартные, нестандартные, показательные, логарифмические, повышенного уровня. Применять основные свойства функции, область определения, область значения функции. Использовать наибольшее и наименьшее значения функции. Применение производной. Я считаю, что цели которые поставлены перед выполнением курсовой работы выполнены.
Литература
О.В. Харькова «Иррациональные уравнения».
А.Н. Колмогоров «Алгебра и начала анализа».
Е.Д. Куланин, В.П. Норин «3000 конкурсных задач по математике».
В.А. Гусев, А.Г. Мордкович «Справочные материалы по математике».
М.И. Сканави «Сборник задач по математике».
Похожие работы
... введение нового(новых) неизвестного. Пример 2. Обозначим , тогда а) Уравнение примет вид: Корень не удовлетворяет условию Ответ: 76. Методы решения иррациональных уравнений. Методы решения иррациональных уравнений, как правило основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному, либо ...
... , т.к. . б) , т.к. . в) . Выясним, при каких n выражения под знаком модуля меняют знак: n=-1, n=1, n=0. 1) Если n<-1, то 2) Если -1£n<0, то 3) Если 0<n<1, то 4) Если n³1, то Ответ: II. Иррациональные уравнения. Рассмотрим уравнение вида . Основной метод решения – возведение обеих частей уравнения в степень n. При этом, если n – четное, то могут возникнуть ...
... по способам решения иррациональных неравенств вида , рассмотрена подробно, изложение теории строгое. Только в учебнике Виленкина рассматривается решение иррационального неравенства вида . Наиболее большой объем упражнений для решения иррациональных уравнений и неравенств представлен в учебниках [11] и [5]. В учебнике [4] упражнений не много, но они разнообразны. Основные понятия, относящиеся к ...
... литературы дается характеристика этих форм, разработана методика применения самостоятельной работы вместе с иными формами организации познавательной деятельности на факультативных занятиях в выпускных классах средней школы, изучены учебные возможности учащихся в экспериментальной группе, проведена опытно- экспериментальная работа по включению самостоятельной работы школьников в процесс обучения. ...
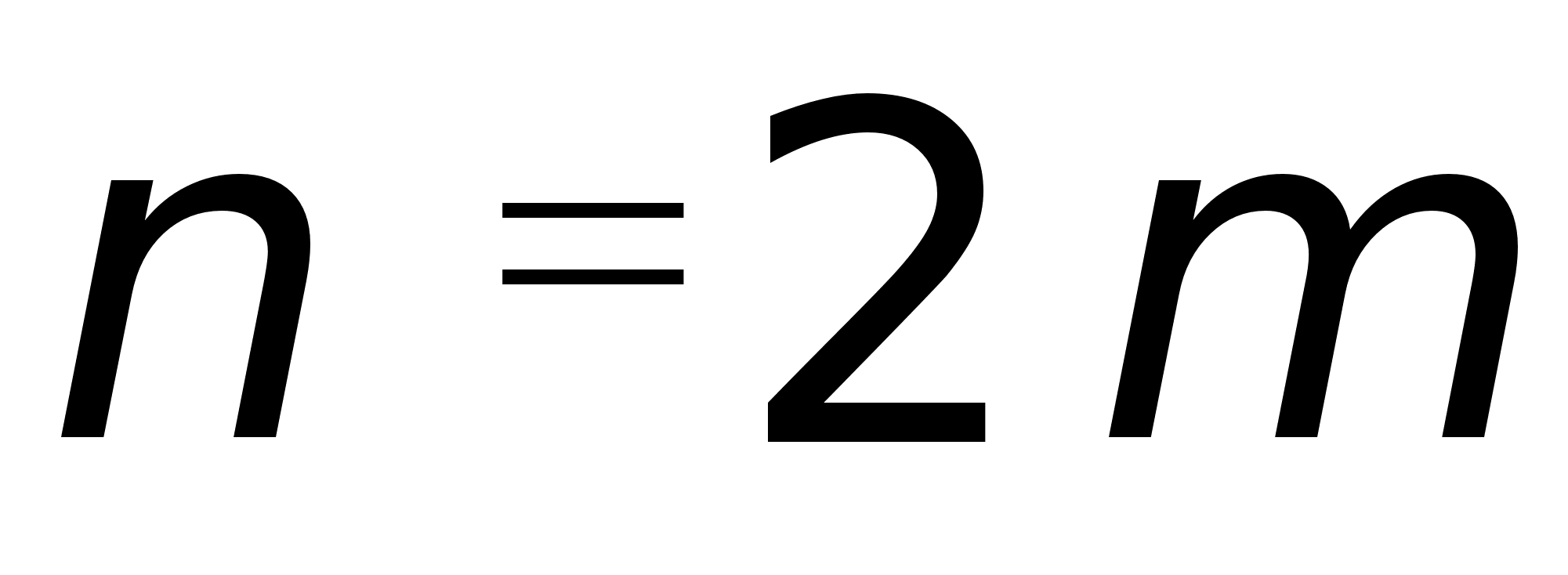
0 комментариев