Навигация
Исследование методов решения системы дифференциальных уравнений с постоянной матрицей
Содержание
1. Введение
2. Постановка задачи
3. Нахождение собственных чисел и построение ФСР 4. Построение фундаментальной матрицы решений методом Эйлера 5. Нахождение приближённого решения в виде матричного ряда6. Построение общего решения матричным методом
7. Задача Коши для матричного метода
8. Решение неоднородной системыГрафики
Заключение
1. Введение
Рассмотрим систему линейных уравнений первого порядка, записанную в нормальной форме:
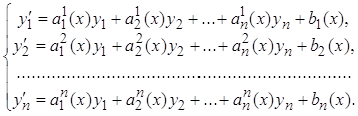 (1)
(1)
где коэффициенты аij, i=1,2,…..,n, к=1,2,…,n, являются постоянными величинами;
yi=yi(t), i=1,2,…,n - неизвестные функции переменной t.
Если все bi(t) (i=1,2,…,n) положить равным нулю (bi(t)=0), то получится однородная система, соответствующая неоднородной системе (1).
Обозначая матрицу системы через А(х), а вектор ![]() через
через ![]() тогда систему (1) можем переписать в матричной форме
тогда систему (1) можем переписать в матричной форме
![]() (1а)
(1а)
Если ![]() , то получаем соответствующую систему однородных уравнений
, то получаем соответствующую систему однородных уравнений
![]() . (2)
. (2)
Всякая совокупность n функций
![]()
![]()
![]()
определенных и непрерывно дифференцируемых в интервале (a;b), называется решением системы (1) в этом интервале, если она обращает все уравнения системы (1) в тождества:
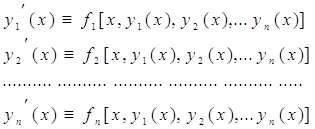
![]()
справедливые при всех значениях x из интервала (a, b). Общее решение неоднородной системы представляет собой сумму общего решения соответствующей однородной системы и частного решения неоднородной.
2. Постановка задачи
Цель работы: исследование методов решения системы дифференциальных уравнений с постоянной матрицей:
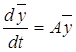 ;
;![]() ;
;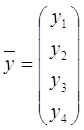
1. Найти собственные числа и построить фундаментальную систему решений (ФСР).
2. Построить фундаментальную матрицу методом Эйлера.
3. Найти приближенное решение в виде матричного ряда.
4. Построить общее решение матричным методом. Исследовать зависимость Жордановой формы матрицы А от ее собственных чисел.
5. Решить задачу Коши.
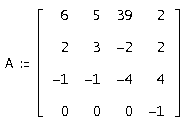
Начальные условия:
Вектор начальных условий: [1, 2, 3, 4]
t = 0
3. Нахождение собственных чисел и построение ФСР
Однородной линейной системой дифференциальных уравнений называется система уравнений вида:
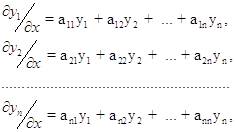 (3)
(3)
Если в матрице системы ![]() все
все ![]() =const, то данная система называется системой с постоянными коэффициентами или с постоянной матрицей.
=const, то данная система называется системой с постоянными коэффициентами или с постоянной матрицей.
Фундаментальной системой решений однородной линейной системы уравнений называется базис линейного пространства решений a, т.е. n линейно независимых решений этой системы.
Для построения фундаментальной системы решений дифференциального уравнения необходимо найти собственные числа характеристического полинома, так как в зависимости от их вида (характеристические числа могут быть действительными разными, кратными, комплексными) строится фундаментальная система решений.
Для того чтобы эта система n линейных однородных уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы определитель системы (вронскиан) был равен нулю:
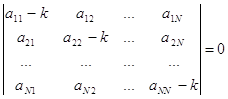 (4)
(4)
Из этого уравнения степени n определяется значение k, при которых система имеет нетривиальные решения. Уравнение (4) называется характеристическим.
Запишем характеристический полином, для этого воспользуемся функцией CHARPOLY
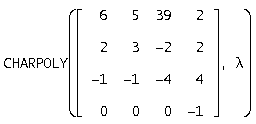
![]()
Для нахождения собственных чисел воспользуемся функцией SOLVE(U, l), которая возвращает характеристические числа матрицы А в вектор l. Получим:
![]()
![]()
Получилось два действительно корня ![]() и два комплексно-сопряженных корня
и два комплексно-сопряженных корня ![]() . Следовательно, вектора, образующие фундаментальную матрицу, для данного типа корней будут находиться отдельно для
. Следовательно, вектора, образующие фундаментальную матрицу, для данного типа корней будут находиться отдельно для ![]() и отдельно для
и отдельно для ![]() . Запишем ФСР для данных для полученных характеристических чисел:
. Запишем ФСР для данных для полученных характеристических чисел:
Матрицу y(x), столбцами которой являются решения, образующие фундаментальную систему, называют фундаментальной матрицей.
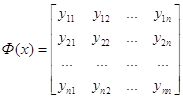
И общее решение системы будет выглядеть следующим образом:
![]()
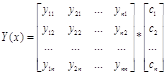
Найдем решение данной системы с помощью метода Эйлера.
4. Построение фундаментальной матрицы решений методом ЭйлераМетод Эйлера заключается в следующем.
Решение системы (1) находится в виде:
![]() (5)
(5)
Функция (5) является решением системы (1), если ![]() – собственное значение матрицы А, а а – собственный вектор этой матрицы, соответствующей числу
– собственное значение матрицы А, а а – собственный вектор этой матрицы, соответствующей числу ![]() . Если собственные значения
. Если собственные значения ![]() 1,
1, ![]() 2, … ,
2, … ,![]() n матрицы А попарно различны и a1, a2, …, anсоответствующие собственные векторы этой матрицы, то общее решение системы уравнений (1) определяется формулой :
n матрицы А попарно различны и a1, a2, …, anсоответствующие собственные векторы этой матрицы, то общее решение системы уравнений (1) определяется формулой :
![]()
где С1, С2, … , Сn – произвольные числа.
Для случая кратных корней решение системы принимает вид
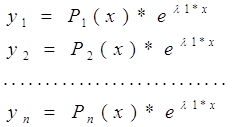 (6)
(6)
где Pi(x)-полиномы степени не выше, чем (к-1), имеющих в совокупности к произвольных коэффициентов. Так что среди коэффициентов этих полиномов к коэффициентов являются произвольными, а оставшиеся к·n-k выражаются через них. Для отыскания коэффициентов полиномов подставим решение (6) в исходную систему уравнений, приравняем коэффициенты при одинаковых функциях. Решим систему по отношению к (k·n-k) коэффициентов. Получим выражение всех коэффициентов через свободные.
Если для кратного собственного значения ![]() матрицы А имеется столько линейно независимых собственных векторов
матрицы А имеется столько линейно независимых собственных векторов ![]() , какова его кратность, то ему соответствует k независимых решений исходной системы:
, какова его кратность, то ему соответствует k независимых решений исходной системы:
![]()
Если для собственного значения ![]() кратности k имеется только m (m<k) линейно независимых собственных векторов, то решения, соответствующие
кратности k имеется только m (m<k) линейно независимых собственных векторов, то решения, соответствующие ![]() , можно искать в виде произведения векторного многочлена степени k - m на
, можно искать в виде произведения векторного многочлена степени k - m на ![]() , т.е. в виде:
, т.е. в виде:
![]()
Чтобы найти векторы ![]() , надо подставить выражение (4) в систему (3). Приравняв коэффициенты подобных членов в левой и правой частях системы, получим уравнение для нахождения векторов
, надо подставить выражение (4) в систему (3). Приравняв коэффициенты подобных членов в левой и правой частях системы, получим уравнение для нахождения векторов ![]() .
.
Для данного задания были найдены следующие собственные значения:
![]() .
.
Построили фундаментальную систему решений:
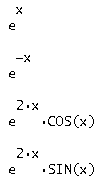
Найдем 1 строку фундаментальной матрицы решений для характеристического числа ![]() . Запишем третью строку решений в общем виде:
. Запишем третью строку решений в общем виде:
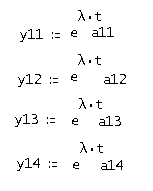
Где аij найдем по выражению:
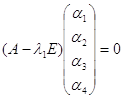 или
или 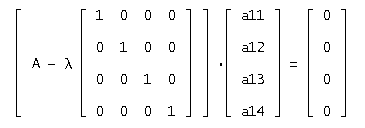
Полученная матрица:
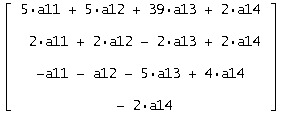
Решаем систему:
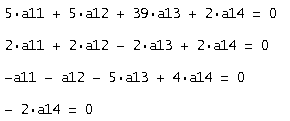
Полученные корни:
![]()
Доопределим ![]()
Тогда первая строка будет иметь вид:
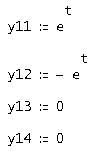
Аналогично найдем вторую строку фундаментальной матрицы решений для первого характеристического числа -1. Полученные значения:
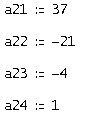
Тогда вторая строка будет иметь вид:
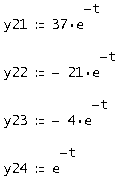
Найдем третью и четвертую строки фундаментальной матрицы решений для первого характеристического числа ![]() . Сопряженный корень
. Сопряженный корень![]() не порождает новых вещественных линейно независимых частных решений.
не порождает новых вещественных линейно независимых частных решений.
Полученные значения:
![]()
Отделяя в нем вещественные и мнимые части, получим два вещественных решения, которые и составляют первую и вторую строки фундаментальной матрицы решений
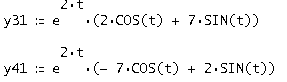
Аналогично остальные 3:
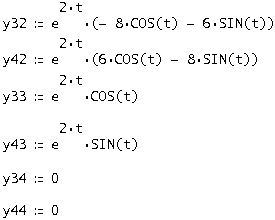
Запишем найденную фундаментальную матрицу решений:
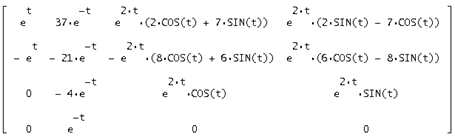
Умножим транспонированную фундаментальную матрицу решений на вектор свободных коэффициентов ![]() и получим вектор общего решения исходной системы:
и получим вектор общего решения исходной системы:
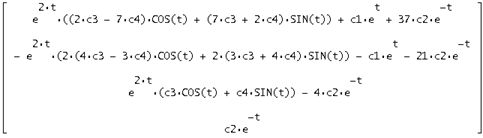
Сделаем проверку найденного решения следующим образом:
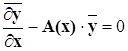
Получаем нулевую матрицу-столбец:
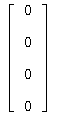 что показывает, что общее решение найдено верно.
что показывает, что общее решение найдено верно.
Дадим определение матричному ряду и экспоненциальной функции матрицы.
Матричные ряды. Рассмотрим бесконечную последовательность матриц ![]() ,
, ![]() ,
,![]() . Будем говорить, что последовательность матриц сходится к матрице А:
. Будем говорить, что последовательность матриц сходится к матрице А:
![]() ,
,
если ![]() при
при ![]() . Из определения нормы следует, что сходимость матриц эквивалентна поэлементной сходимости. Матричным рядом называется символ
. Из определения нормы следует, что сходимость матриц эквивалентна поэлементной сходимости. Матричным рядом называется символ ![]() , причем говорят, что этот ряд сходится к сумме
, причем говорят, что этот ряд сходится к сумме ![]() , если к f сходится последовательность частичных сумм Sk, где
, если к f сходится последовательность частичных сумм Sk, где
. ![]()
Пусть ![]() , тогда можно определить степень матрицы А обычным образом:
, тогда можно определить степень матрицы А обычным образом:
![]() (k раз).
(k раз).
Рассмотрим ряд, называемый степенным:
![]() ,
, ![]() ,
, ![]() ,
,
где по определению положим A0 = En.
Экспоненциальная функция матрицы. В качестве примера рассмотрим степенной ряд, равный:
![]() .
.
Так как радиус сходимости соответствующего числового ряда
![]()
Равен бесконечности, то ряд сходится при всех А. Сумма ряда называется экспоненциальной функцией (экспонентой) и обозначается через еА, если ехр{А}.
Приближенно вектор решений можно найти как произведение матричного ряда:
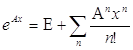
и вектора начальных условий y0=[y1,y2, …..yk].
Формула является матричной задачей Коши в приближенном виде.
Экспонентой ![]() матрицы А называется сумма ряда
матрицы А называется сумма ряда
![]()
где Е – единичная матрица.
Матрица ![]() является решением матричной задачи Коши:
является решением матричной задачи Коши:
![]() т.е. является фундаментальной матрицей системы.
т.е. является фундаментальной матрицей системы.
Найдем разложение матричного ряда последовательно по семи, восьми и десяти первым членам.
для получения разложения по 7 первым членам (аналогично по 8,10 и 10). Результатом будет являться матрица 4*4. Полученные матрицы умножаем на вектор начальных условий S=[1,2,3,4] и получаем приближенное решение в виде матричного ряда.




При увеличении членов разложения ряда вектор приближенных решений будет стремиться к вектору точных решений. Этот факт можно наблюдать, графически сравнивая изображение точного и приближенного решений (см. приложение).
Умножим на соответствующий вектор начальных условий и получим приближенное решение в виде матричного ряда, запишем полученное решение для n=7.
[s1 ≔ 1, s2 ≔ 2, s3 ≔ 3, s4 ≔ 4]

Похожие работы
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
... , является важнейшей вспомогательной научно-технической задачей . Целью данной курсовой работы является разработка алгоритма решения систем линейных дифференциальных уравнений первого порядка пяти точечным методом прогноза и коррекции Адамса-Башфорта . 1. ПОСТАНОВКА ЗАДАЧИ Рассмотрим произвольную систему линейных дифференциальных уравнений первого порядка : ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
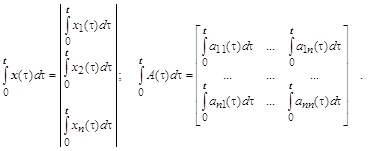
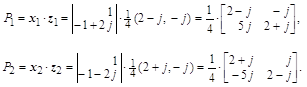
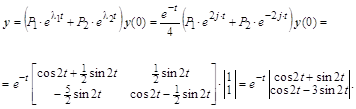
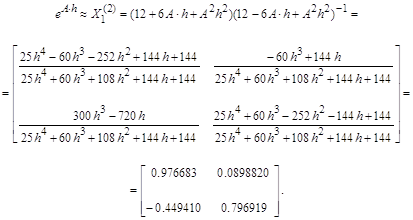
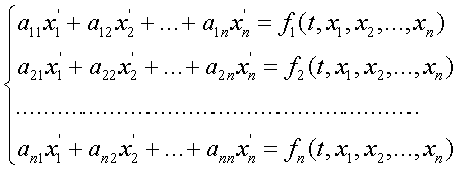
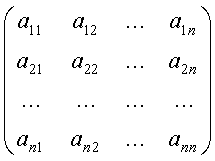
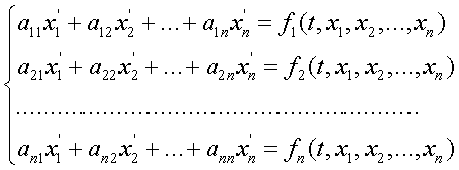
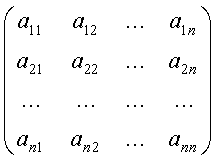
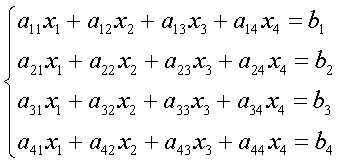
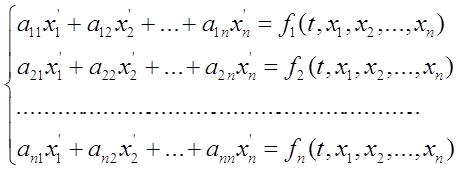

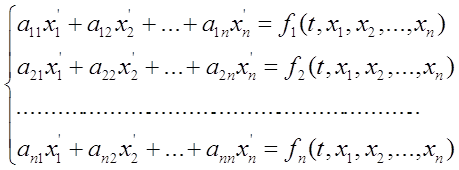
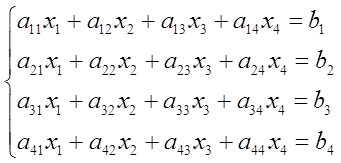
0 комментариев