Навигация
Задача Коши для матричного метода
7. Задача Коши для матричного метода
Необходимо из всех решений системы уравнений найти такое решение, в котором y(i)(t) принимает заданное числовое значение y0iв заданной точке, т.е. найти значения сi для следующих заданных значений: x=0, y=[1, 2, 3,4].
В вектор решений y(t) подставляем заданные условия и решаем полученную систему относительно c1, c2, c3, c4:
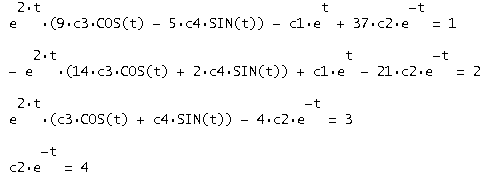
В результате получаем:
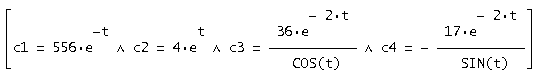
При подстановке c1, c2, c3, c4в общее решение получим решение в форме Коши:
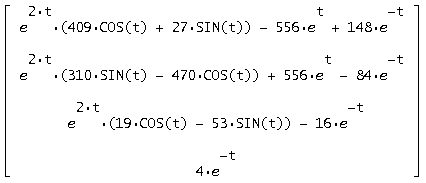

Получился нулевой вектор ![]() . Следовательно, найденная матрица является решением исходной системы.
. Следовательно, найденная матрица является решением исходной системы.
Пусть J – жорданова клетка матрицы А. Для случая действительных разных корней жорданова клетка будет выглядеть следующим образом:
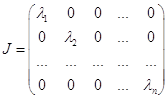
Пусть среди действительных собственных чисел матрицы А есть кратные. Жорданова клетка будет находиться по следующей формуле:
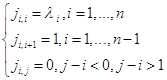
Например, если кратность k=2, то жорданову клетку матрицы мы можем записать так:
![]()
Если кратность k=3, то жорданову клетку матрицы мы можем записать так:
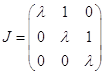
Если же среди трех собственных чисел ![]() являются корнями кратности 2, то жорданова форма будет выглядеть следующим образом:
являются корнями кратности 2, то жорданова форма будет выглядеть следующим образом:
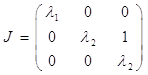
Если два собственных числа матрицы А являются комплексными сопряженными, то запись жордановой клетки будет выглядеть так:
![]()
где ![]() – действительная,
– действительная, ![]() – мнимая часть собственного числа
– мнимая часть собственного числа ![]() .
.
Общее решение неоднородной системы можно найти по формуле:
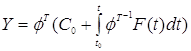
Где ![]() - фср, Со – матрица
- фср, Со – матрица 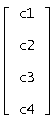 , F(t) – вектор правых части.
, F(t) – вектор правых части.
![]() - общее решение однородной системы
- общее решение однородной системы
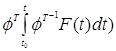 - частное решение неоднородной системы
- частное решение неоднородной системы Полученное частное решение неоднородной системы:
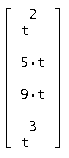
Общее решение однородной системы
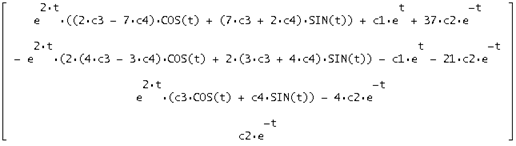
Тогда их сумма будет искомым общим решением неоднородной системы:
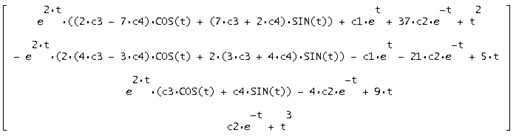
Проверим

Найденное решение верно.
Графики
Изобразим графически точное частное решение однородной линейной системы дифференциальных уравнений с постоянными коэффициентами для начальных условий: t0 = 0, y0 = [1, 2, 3, 4].
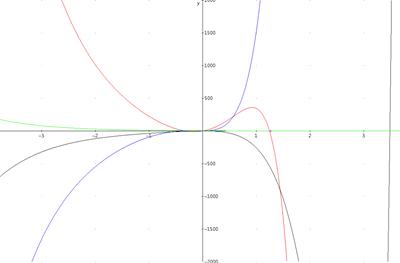
Сравним график одной функции вектора точного решения и одной функции вектора приближенного решения с 3-мя, 5-ю и 7-ю членами ряда:
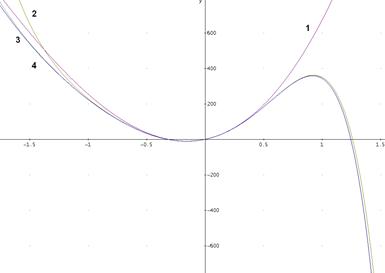
Где 1 – график приближенного решения для трех членов ряда; 2 – график приближенного решения для шести членов ряда; 3 – график приближенного решения для девяти членов ряда; 4 – график точного решения.
Можно сделать вывод:
С увеличением числа членов ряда, число совпадения членов ряда с точным решением будет увеличиваться, область совпадения будет расти.
Заключение
В ходе проделанной работы было изучено 3 метода нахождения общего решения однородной системы линейных дифференциальных уравнений: метод Эйлера, решение в виде матричного ряда и матричный метод. По сравнению с методом Эйлера и матричным методом, метод разложения в матричный ряд прост в реализации, но дает приближенное решение. Также была изучена задача Коши, которая была использована для нахождения частного решения однородной системы линейных дифференциальных уравнений для данного вида начальных условий.
Для установления правильности проведенных вычислений была проведена проверка с помощью подстановки полученных решений в исходную систему уравнений.
Для реализации этой работы в DERIVE были использованы следующие функции пакета:
1. EIGENVALUES (A, ![]() ) – вычисление собственных чисел матрицы A с последующей записью в вектор
) – вычисление собственных чисел матрицы A с последующей записью в вектор ![]() .
.
2. SOLVE (Pm=0, ![]() ) – решение уравнения Pm=0, где Pm – полином степени m: Pm=p0*
) – решение уравнения Pm=0, где Pm – полином степени m: Pm=p0*![]() mp1*
mp1*![]() m-1+…+pm-1*
m-1+…+pm-1*![]() +pm, а
+pm, а ![]() - переменная, относительно которой решается данное уравнение.
- переменная, относительно которой решается данное уравнение.
3. EXACT_VECTOR(A, ![]() ) – вычисление точного собственного вектора матрицы А и размещение этих значений в
) – вычисление точного собственного вектора матрицы А и размещение этих значений в ![]() .
.
4. DIF(A,x,n) – дифференцирование A по x n раз.
5. SUM(M,n,f,g) – вычисление суммы M по n изменяющимся с f до g.
6. VECTOR(u,k,n)– задание (вычисление) вектора значений при k изменяющемся от 1 до n.
А также функции меню:
1. SOLVE/SYSTEM –решение системы с последующим заданием в диалоговом окне количества уравнений, самих уравнений и переменных, относительно которых решается данное уравнение.
2. Simplify > Expand– раскрытие выражений.
Команда Expand используется для раскрытия математических выражений.
Expand expression: #n: где n – номер строки выражения (операнда).
Expand Variable: #n .
В этом варианте команды необходимо указать имя переменной, по которой будет проведено преобразование. Если по всем -<Enter>.
3. Для построения графиков использовали функцию 2D-plot.
Похожие работы
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
... , является важнейшей вспомогательной научно-технической задачей . Целью данной курсовой работы является разработка алгоритма решения систем линейных дифференциальных уравнений первого порядка пяти точечным методом прогноза и коррекции Адамса-Башфорта . 1. ПОСТАНОВКА ЗАДАЧИ Рассмотрим произвольную систему линейных дифференциальных уравнений первого порядка : ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
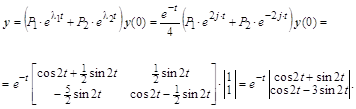
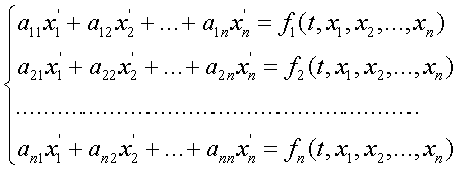
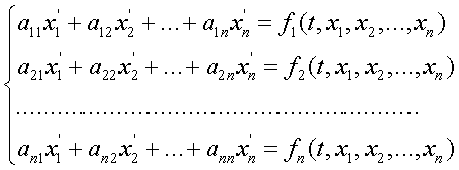

0 комментариев