Навигация
Построение общего решения матричным методом
6. Построение общего решения матричным методом
Матричный метод решения системы уравнений (1) основан на непосредственном отыскании фундаментальной матрицы этой системы.
![]()
Экспонентой eA матрицы А называется сумма ряда
где Е – единичная матрица.
Свойство матричной экспоненты:
а) если АВ=ВА, то еА+В=еА*еВ= еВ *еА;
б) если А=S-1*B*S, то еА=S-1*eB*S, где матрица S – это матрица преобразования переменных из собственного базиса в базис исходных переменных.
в) матрица y(t)=eAt является решением матричной задачи Коши:
т.е. является фундаментальной матрицей системы (1).
Из свойства в) следует, что решение y(t) системы (1) удовлетворяющее условию y(0)=y0, определяется выражением y(t)=eAt*y0. Таким образом, задача нахождения решений системы уравнений (1) эквивалентна задачи отыскания матрицы eAt по матрице А.
Для вычисления матрицы eAt удобно представить матрицу А в виде:
![]() ,
,
где матрица S – это матрица преобразования переменных из собственного базиса в базис исходных переменных, а BА – жорданова форма матрицы А, т.к. eAt= S-1*eBt*S.
Жорданова форма матрицы зависит от вида характеристических чисел.
1. Пусть характеристические числа действительные кратные, тогда Жорданова форма матрицы размерности nxn имеет вид:
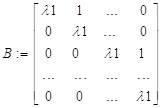
где ![]() - действительный корень кратности n.
- действительный корень кратности n.
2. Если среди корней характеристического полинома имеются, как действительные разные, так и действительные кратные корни, то матрица В имеет вид:
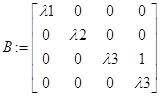
где ![]() - действительные разные корни, а
- действительные разные корни, а ![]() - действительный корень кратности 2.
- действительный корень кратности 2.
3. При наличии среди корней характеристического полинома корней комплексно-сопряженных Жорданова клетка выглядит следующим образом:
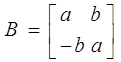
где а ![]() комплексно сопряженный корень характеристического полинома.
комплексно сопряженный корень характеристического полинома.
Так как в нашем случае среди характеристических чисел присутствуют, как комплексно-сопряженные корни л = 2 - ∨ л = 2 + , так и действительный разные корни л = -1 ∨ л = 1,то жорданова матрица выглядит следующим образом:
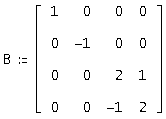
Из уравнения A*S = S*В, где S – невырожденная матрица, получаем систему 16-го порядка, из которой находим элементы матрицы S. Полученная матрица S будет выглядеть следующим образом:

Решаем систему 16-го порядка из уравнения A*S = S*В

Доопределяем некоторые элементы и получаем следующую матрицу S:

Сделаем проверку A*S - S*В=0:
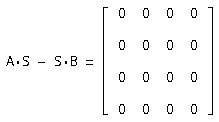
Значит матрица перехода найдена верно.
Для нахождения вектора решений y необходимо умножить матрицу S на ![]() , где
, где ![]() - это вектор, элементы которого зависят от корней характеристического многочлена:
- это вектор, элементы которого зависят от корней характеристического многочлена:
![]()
Для комплексных чисел ![]() имеет следующий вид:
имеет следующий вид:
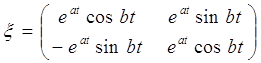
Для случая корней действительных разных:
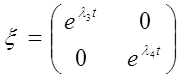
В нашем случае ![]() получается равной:
получается равной:
![]() =
=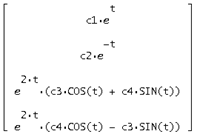
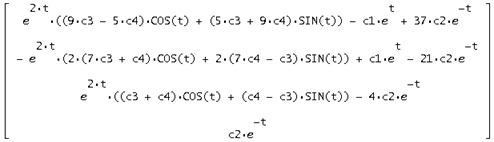
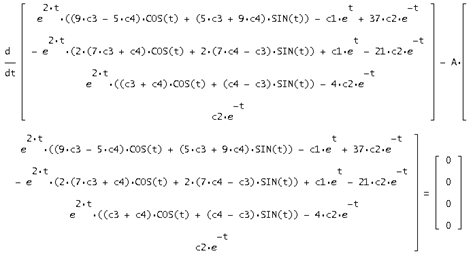
Похожие работы
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
... , является важнейшей вспомогательной научно-технической задачей . Целью данной курсовой работы является разработка алгоритма решения систем линейных дифференциальных уравнений первого порядка пяти точечным методом прогноза и коррекции Адамса-Башфорта . 1. ПОСТАНОВКА ЗАДАЧИ Рассмотрим произвольную систему линейных дифференциальных уравнений первого порядка : ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
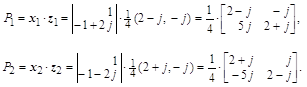
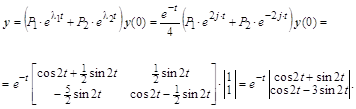
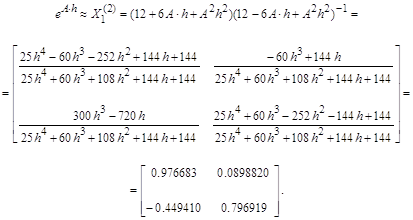
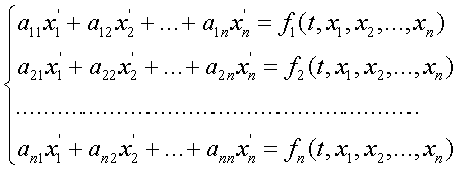
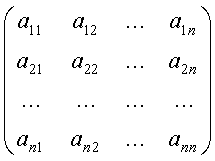
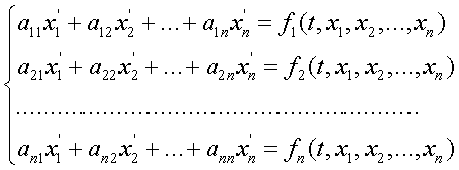
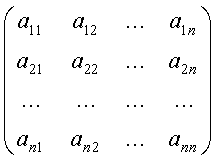
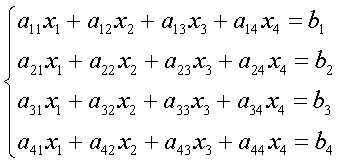
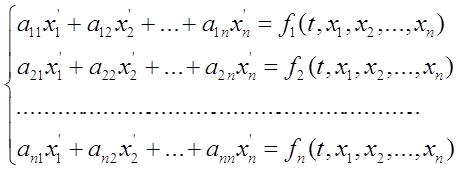

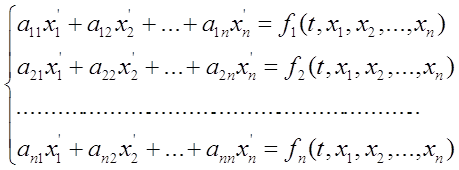
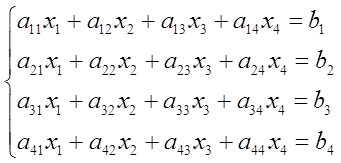
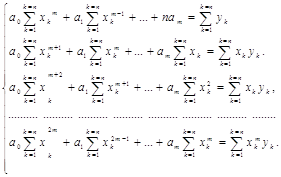
0 комментариев