Навигация
2. ИССЛЕДОВАНИЕ ФУНКЦИЙ
2.1 Достаточные условия экстремума функции
В лекции 1 мы рассмотрели основные теоремы математического анализа, которые широко используются при исследовании функции, построении ее графика.
По теореме Ферма: из дифференцируемости функции f(x) в точке локального экстремума х0 следует, что f'(x0) = 0. Данное условие является необходимым условием существования в точке локального экстремума, то есть если в точке х0 – экстремум функции f(x) и в этой точке существует производная, то f'(x0) = 0. Точки х0, в которых f'(x0) = 0, называются стационарными точками функции. Заметим, что равенство нулю производной
в точке не является достаточным для существования локального экстремума в этой точке.
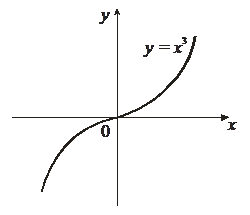
Пример 1. у = х3, у' = 3х2, у'(0) = 0, но
в точке х0 = 0 нет экстремума.
Точками, подозрительными на экстремум функции f(x) на интервале (a, b), являются точки, в которых производная существует и равна 0 либо она не существует или равна бесконечности. На рисунках функции имеют минимум в точке х0 = 0:
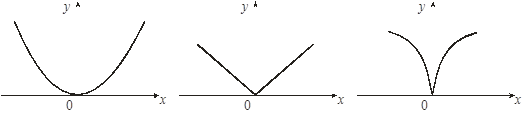
f '(0) = 0 f '(0) $ f '(0) = ¥
Рассмотрим достаточные условия существования в точке локального экстремума, которые позволят ответить на вопрос: «Есть ли в точке экстремум и какой именно – минимум или максимум?».
Теорема 1 (первое достаточное условие экстремума). Пусть непрерывная функция f(x) дифференцируема в некоторой проколотой окрестности U(x0) точки х0 (проколотая окрестность означает, что сама точка х0 выбрасывается из окрестности) и непрерывна в точке х0. Тогда:
1) если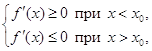 
(1)
то в точке х0 – локальный максимум;
2) если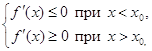 
(2)
то в точке х0 – локальный минимум.
Доказательство.
Из неравенств (1) и следствия 3 теоремы Лагранжа (о монотонности функции) следует, что при х < х0 функция не убывает, а при х > х0 функция не возрастает, то есть
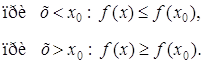(3)
Следовательно, из (3) получаем, что в точке х0 функция имеет локальный максимум.
Аналогично можно рассмотреть неравенства (2) для локального минимума:
 |
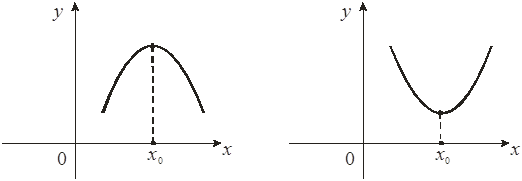f (x) f (x)
f '(х) ³ 0 f '(х) £ 0 f '(х) £ 0 f '(х) ³ 0
Теорема доказана.
Пример 2. Исследовать на монотонность и локальный экстремум функцию 
с помощью производной первого порядка.
Решение. Найдем стационарные точки функции:
Þ х2 –1 = 0 Þ х1 = –1, х2 = 1.
Заметим, что данная функция не определена в точке х = 0. Следовательно:
| х | (–¥; –1) | –1 | (–1; 0) | 0 | (0; 1) | 1 | (1; +¥) |
| у' | + | 0 | – | – | – | 0 | + |
| у |
| –2 |
| – |
| 2 |
|
max min
То есть функция возрастает на интервалах (–¥; –1) и (1; +¥), убывает на интервалах (–1; 0), (0; 1), имеет локальный максимум в точке
х1 = –1, равный уmax (–1) = –2; имеет локальный минимум в точке х2 = 1,
уmin (1) = 2.
Теорема 2 (второе достаточное условие экстремума). Пусть функция f (x) дважды непрерывно-дифференцируема. Если х0 – стационарная точка
(f ' (х0) = 0), в которой f '' (х0) > 0, то в точке х0 функция имеет локальный минимум. Если же f '' (х0) < 0, то в точке х0 функция имеет локальный максимум.
Доказательство. Пусть для определенности f '' (х0) > 0. Тогда
Следовательно:
при х < х0, f ' (х) < 0,
при х > х0, f ' (х) > 0.
Поэтому по теореме 1 в точке х0 функция имеет локальный минимум.
Теорема доказана.
Пример 3. Исследовать на экстремум функцию с помощью второй производной.
Решение. В примере 2 для данной функции мы нашли первую производную 
и стационарные точки х1 = –1, х2 = 1.
Найдем вторую производную данной функции:
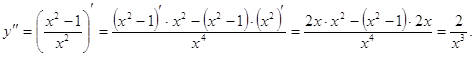
Найдем значения второй производной в стационарных точках.
Þ в точке х1 = –1 функция имеет локальный максимум;
Þ в точке х2 = 1 функция имеет локальный минимум (по теореме 2).
Заметим, что теорема 1 более универсальна. Теорема 2 позволяет проанализировать на экстремум лишь точки, в которых первая производная равна нулю, в то время как теорема 1 рассматривает три случая: равенство производной нулю, производная не существует, равна бесконечности в подозрительных на экстремум точках.
Похожие работы
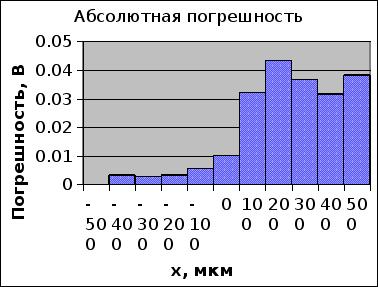
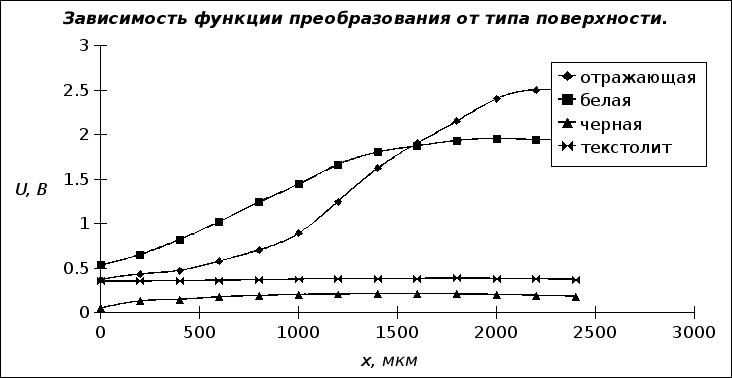
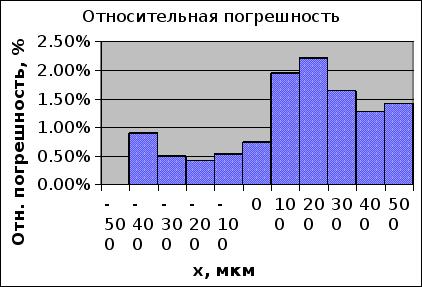
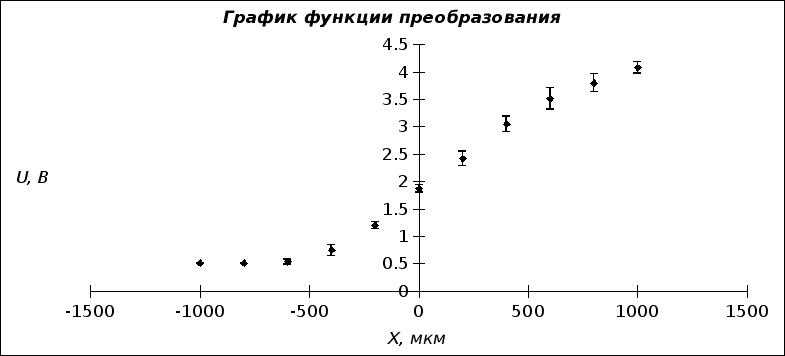
... образованию Московский государственный институт электроники и математики Кафедра ЭВА Лабораторная работа по курсу "Метрология и измерительная техника" Исследование функций преобразования и метрологических характеристик бесконтактных волоконно-оптических датчиков перемещений. Выполнили студенты группы С-45 Голышевский А. Костарев В. Куприянов Ю. Сапунов Г. Преподаватель Зак Е.А. Москва ...
... пунктах были рассмотрены методы исследования поведения функции с помощью производной. Однако среди вопросов, касающихся полного исследования функции, есть и такие, которые с производной не связаны. Так, например, необходимо знать, как ведет себя функция при бесконечном удалении точки ее графика от начала координат. Такая проблема может возникнуть в двух случаях: когда аргумент функции уходит на ...
... , уменьшением отека и размеров лимфатических узлов, наблюдается заметное уменьшение секреции и кислотности желудочного сока. Признаки заметного раздражения нервной системы исчезают. Повторные исследования секреторной функции желудка позволяют выяснить, что после 1—2-недельного лечения стрептомицином секреторная функция желудка резко усиливается, а инсулин вызывает исключительно сильное отделение ...
... и вентиляционной недостаточности, проследить динамику изменений функций внешнего дыхания в процессе лечения больного. Исследование функции внешнего дыхания проводятся с целью определения типа и тяжести вентиляционных нарушений, уточнения тяжести нарушений газового состава крови. В клинике используются методы определения статических и динамических показателей функции внешнего дыхания, такие как ...
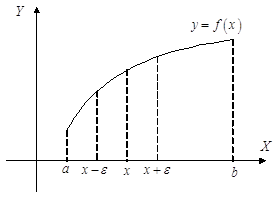
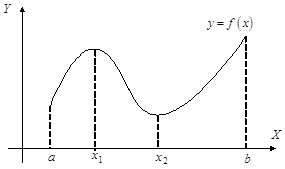
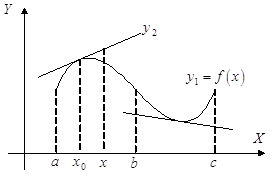
0 комментариев