Навигация
Асимптоты графика функции
2.3 Асимптоты графика функции
Асимптотой будем называть прямую, к которой график функции неограниченно близко приближается. Различают вертикальные и наклонные асимптоты.
Прямая х = х0 называется вертикальной асимптотой графика функции f(х), если хотя бы один из пределов f(х0 – 0) или f(х0 + 0) равен бесконечности.
Пример 6. Найти вертикальные асимптоты функций:
а) ![]() б)
б) 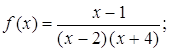 в)
в) 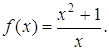
Решение. Вертикальными асимптотами функций будут прямые х = х0, где х0 – точки, в которых функция не определена.
а) х = 3 – вертикальная асимптота функции ![]() . Действительно,
. Действительно, ![]() ;
;
б) х = 2, х = –4 – вертикальные асимптоты функции 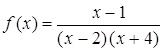 . Действительно,
. Действительно,
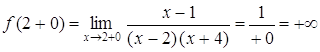 ,
,
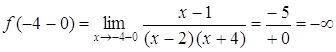 ;
;
в) х = 0 – вертикальная асимптота функции 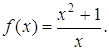 Действительно,
Действительно, 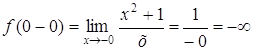 .
.
Прямая у = kx + b называется наклонной асимптотой графика непрерывной функции f(х) при х ® +¥ или х ® –¥, если f(х) = kx + b + α(х), ![]() , то есть если наклонная асимптота для графика функции f(х) существует, то разность ординат функции f(х) и прямой у = kx + b в точке х стремится к 0 при х ® +¥ или при х ® –¥.
, то есть если наклонная асимптота для графика функции f(х) существует, то разность ординат функции f(х) и прямой у = kx + b в точке х стремится к 0 при х ® +¥ или при х ® –¥.
Теорема 6. Для того чтобы прямая у = kx + b являлась наклонной асимптотой графика функции f(х) при х ® +¥ или х ® –¥, необходимо и достаточно существование конечных пределов:
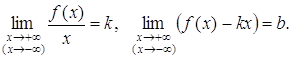 (4)
(4)
Следовательно, если хотя бы один из данных пределов не существует или равен бесконечности, то функция не имеет наклонных асимптот.
Пример 7. Найти наклонные асимптоты функции ![]()
Решение. Найдем пределы (4):
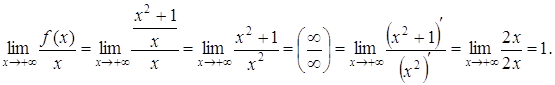
Следовательно, k = 1.
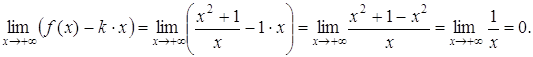
Следовательно, b = 0.
Таким образом, функция ![]() имеет наклонную асимптоту
имеет наклонную асимптоту
у = kx + b = 1 · х + 0 = х.
Ответ: у = х – наклонная асимптота.
Пример 8. Найти асимптоты функции 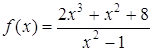 .
.
Решение.
а) функция неопределенна в точках х1 = –1, х2 = 1. Следовательно, прямые х1 = –1, х2 = 1 – вертикальные асимптоты данной функции.
Действительно, 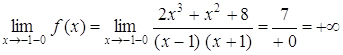 .
.
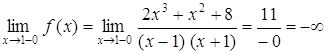 ;
;
б) у = kx + b.
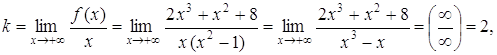
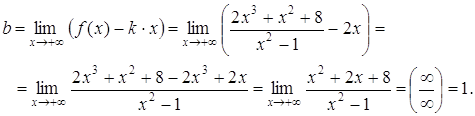
Следовательно, у = 2х + 1 – наклонная асимптота данной функции.
Ответ: х1 = –1, х2 = 1 – вертикальные, у = 2х + 1 – наклонная асимп-
тоты.
2.4 Общая схема построения графика функции
1. Находим область определения функции.
2. Исследуем функцию на периодичность, четность или нечетность.
3. Исследуем функцию на монотонность и экстремум.
4. Находим промежутки выпуклости и точки перегиба.
5. Находим асимптоты графика функции.
6. Находим точки пересечения графика функции с осями координат.
7. Строим график.
Прежде чем перейти к примерам, напомним определения четности и нечетности функции.
Функция у = f(х) называется четной, если для любого значения х, взятого из области определения функции, значение (–х) также принад-лежит области определения и выполняется равенство f(х) = f(–х). График четной функции симметричен относительно оси ординат.
Функция у = f(х) называется нечетной для любого значения х, взятого из области определения функции, значение (–х) также принадлежит об-ласти определения, и выполняется равенство f(–х) = –f(х). График не-четной функции симметричен относительно начала координат.
Пример 9. Построить график ![]() .
.
Решение. Мы используем данные, полученные для этой функции в других примерах.
Похожие работы
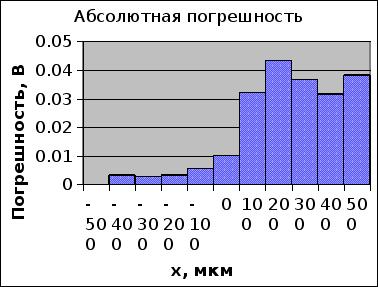
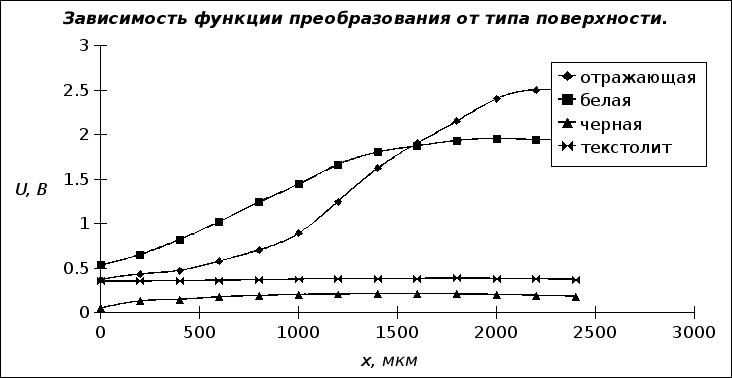
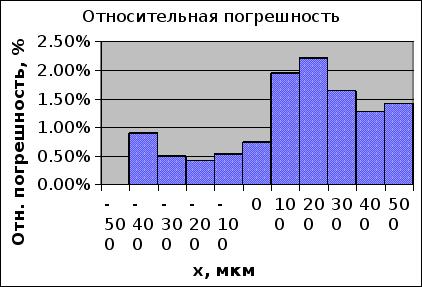
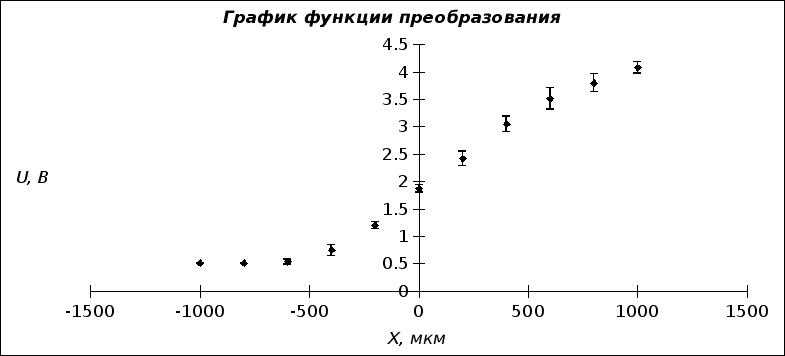
... образованию Московский государственный институт электроники и математики Кафедра ЭВА Лабораторная работа по курсу "Метрология и измерительная техника" Исследование функций преобразования и метрологических характеристик бесконтактных волоконно-оптических датчиков перемещений. Выполнили студенты группы С-45 Голышевский А. Костарев В. Куприянов Ю. Сапунов Г. Преподаватель Зак Е.А. Москва ...
... пунктах были рассмотрены методы исследования поведения функции с помощью производной. Однако среди вопросов, касающихся полного исследования функции, есть и такие, которые с производной не связаны. Так, например, необходимо знать, как ведет себя функция при бесконечном удалении точки ее графика от начала координат. Такая проблема может возникнуть в двух случаях: когда аргумент функции уходит на ...
... , уменьшением отека и размеров лимфатических узлов, наблюдается заметное уменьшение секреции и кислотности желудочного сока. Признаки заметного раздражения нервной системы исчезают. Повторные исследования секреторной функции желудка позволяют выяснить, что после 1—2-недельного лечения стрептомицином секреторная функция желудка резко усиливается, а инсулин вызывает исключительно сильное отделение ...
... и вентиляционной недостаточности, проследить динамику изменений функций внешнего дыхания в процессе лечения больного. Исследование функции внешнего дыхания проводятся с целью определения типа и тяжести вентиляционных нарушений, уточнения тяжести нарушений газового состава крови. В клинике используются методы определения статических и динамических показателей функции внешнего дыхания, такие как ...
0 комментариев