Навигация
Исследование функций на выпуклость и вогнутость. Точка перегиба
19723
знака
8
таблиц
16
изображений
2.2 Исследование функций на выпуклость и вогнутость. Точка перегиба
Пусть функция f (х) задана на интервале (a, b) и х1, х2 – любые различные точки этого интервала. Через точки А (х1, f(х1)) и В (х2, f(х2)) графика функции f(х) проведем прямую, отрезок АВ которой называется хордой. Уравнение этой прямой запишем в виде у = у(х).
Функция f(х) называется выпуклой вниз на интервале (a, b), если для любых точек х1, х2 Î (a, b), а £ х1 < х2 £ b, хорда АВ лежит не ниже графика этой функции, т. е. если f(х) £ у (х), х Î [х1, х2] Ì (a, b):
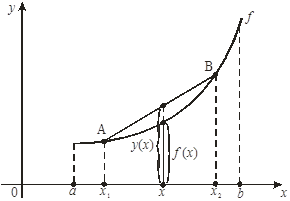
Заметим, что выпуклую вниз функцию иногда называют вогнутой функцией. Аналогично определяется выпуклость функции вверх.
Функция f(х) называется выпуклой вверх на интервале (a, b), если для любых точек х1, х2 Î (a, b), а £ х1 < х2 £ b, хорда АВ лежит не выше графика этой функции, т. е. если f(х) ³ у (х), х Î [х1, х2] Ì (a, b):
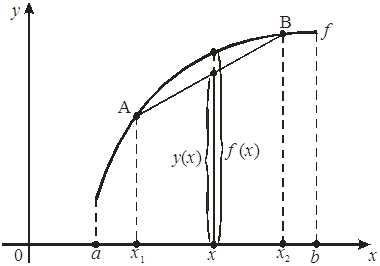
Теорема 3 (достаточное условие выпуклости). Если f(х) – дважды непрерывно дифференцируема на интервале (a, b) и
1) f ''(х) > 0, х Î (a, b), то на (a, b) функция f(х) выпукла вниз;
2) f ''(х) < 0, х Î (a, b), то на (a, b) функция f(х) выпукла вверх.
Точка х0 называется точкой перегиба функции f(х), если $ d – окрест-ность точки х0, что для всех х Î (х0 – d, х0) график функции находится с одной стороны касательной, а для всех х Î (х0, х0 + d) – с другой стороны каса-тельной, проведенной к графику функции f(х) в точке х0, то есть точка х0 – точка перегиба функции f(х), если при переходе через точку х0 функция f(х) меняет характер выпуклости:
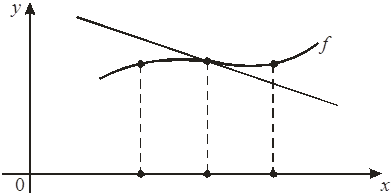
х0 – d х0 х0 + d
Теорема 4 (необходимое условие существования точки перегиба). Если функция f(х) имеет непрерывную в точке х0 производную f '' и х0 – точка перегиба, то f '' (х0) = 0.
Доказательство.
Если бы f '' (х0) < 0 или f '' (х0) > 0, то по теореме 3 в точке х0 функция f(х) была бы выпукла вверх или вниз. Следовательно, f ''(х0) = 0.
Теорема доказана.
Теорема 5 (достаточное условие перегиба). Если функция f(х) дважды непрерывно дифференцируема в окрестности точки х0 и при переходе через точку х0 производная f ''(х) меняет знак, то точка х0 является точкой перегиба функции f(х).
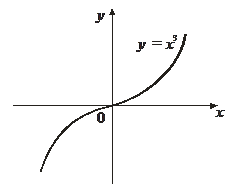
Пример 4. Исследовать на выпуклость и найти точки перегиба функции у = х3.
Решение. у' = 3х2, у'' = 6х = 0 Þ х0 = 0 – точка, подозрительная на перегиб.
В точке х0 = 0 функция у = х3 имеет перегиб:
| х | (–¥; 0) | 0 | (0; +¥) |
| у'' | – | 0 | + |
| у | выпукла вверх | 0 | выпукла вниз |
| точка перегиба |
Пример 5. Исследовать на выпуклость и найти точки перегиба функции 
.
Решение. В примере 3 мы уже находили вторую производную данной функции 
. Так как 
то точек подозрительных на перегиб нет. Рассмотрим промежутки выпуклости:
| х | (–¥; 0) | 0 | (0; +¥) |
| у'' | – | – | + |
| у | выпукла вверх | – | выпукла вниз |
| функция не определена |
Похожие работы
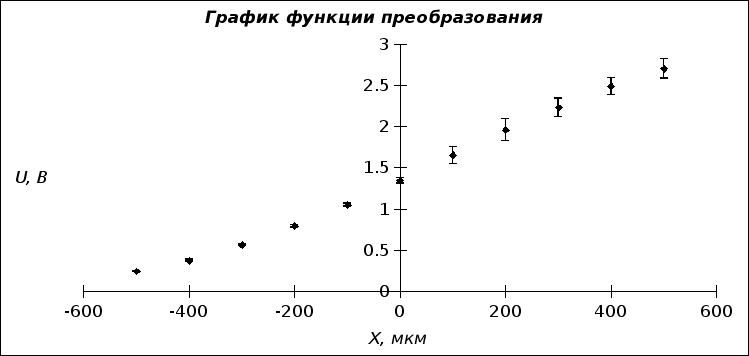
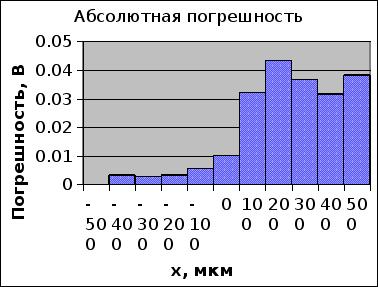
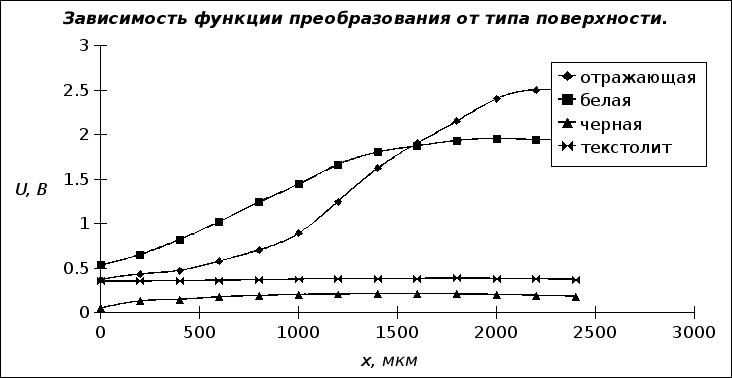
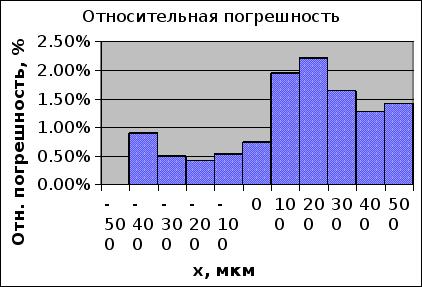
... образованию Московский государственный институт электроники и математики Кафедра ЭВА Лабораторная работа по курсу "Метрология и измерительная техника" Исследование функций преобразования и метрологических характеристик бесконтактных волоконно-оптических датчиков перемещений. Выполнили студенты группы С-45 Голышевский А. Костарев В. Куприянов Ю. Сапунов Г. Преподаватель Зак Е.А. Москва ...
... пунктах были рассмотрены методы исследования поведения функции с помощью производной. Однако среди вопросов, касающихся полного исследования функции, есть и такие, которые с производной не связаны. Так, например, необходимо знать, как ведет себя функция при бесконечном удалении точки ее графика от начала координат. Такая проблема может возникнуть в двух случаях: когда аргумент функции уходит на ...
... , уменьшением отека и размеров лимфатических узлов, наблюдается заметное уменьшение секреции и кислотности желудочного сока. Признаки заметного раздражения нервной системы исчезают. Повторные исследования секреторной функции желудка позволяют выяснить, что после 1—2-недельного лечения стрептомицином секреторная функция желудка резко усиливается, а инсулин вызывает исключительно сильное отделение ...
... и вентиляционной недостаточности, проследить динамику изменений функций внешнего дыхания в процессе лечения больного. Исследование функции внешнего дыхания проводятся с целью определения типа и тяжести вентиляционных нарушений, уточнения тяжести нарушений газового состава крови. В клинике используются методы определения статических и динамических показателей функции внешнего дыхания, такие как ...
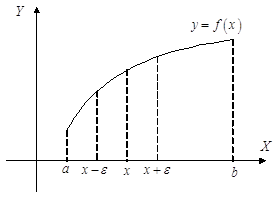
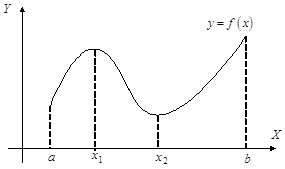
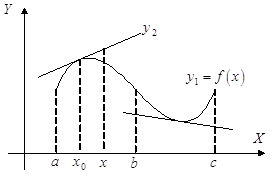
0 комментариев