Навигация
Зная параметры "а" и "в" и пользуясь табулированными функциями аf(t) и F(t), можно определить дифференциальную и интегральную функции
4. Зная параметры "а" и "в" и пользуясь табулированными функциями аf(t) и F(t), можно определить дифференциальную и интегральную функции.
При нахождении функции f(t) для каждого интервала статистического ряда определяется отношение ![]() , где tci – середина i-го интервала. По найденному отношению при определенной величине параметра "в" по таблице определяем значение функции аf(tci-tсм), нормированной по "а".
, где tci – середина i-го интервала. По найденному отношению при определенной величине параметра "в" по таблице определяем значение функции аf(tci-tсм), нормированной по "а".
Значение функции f(t) для i-го интервала статистического ряда определится из выражения:
![]() (1.22)
(1.22)
Для нахождения функции F(t) для каждого интервала определяется отношение ![]() , где tкi – конец i-го интервала. По найденному отношению и параметру "в" по таблице определяем значение интегральной функции F(tкi – tсм).
, где tкi – конец i-го интервала. По найденному отношению и параметру "в" по таблице определяем значение интегральной функции F(tкi – tсм).
Для данного задания значение дифференциальной и интегральной функций при ЗРВ будут равны:
для первого интервала
![]()
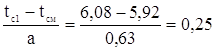 в=2,5
в=2,5 ![]()
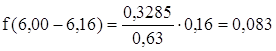
![]()
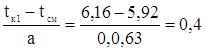 в=2,5 F(tк1)= 0,096
в=2,5 F(tк1)= 0,096
для второго интервала
![]()
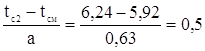 в=2,5
в=2,5 ![]()
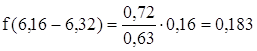
![]()
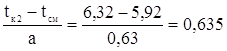 в=2,5 F(tк1)=0,243
в=2,5 F(tк1)=0,243
Дальнейшие результаты расчетов представлены в таблице 1.4.
Графическое изображение дифференциальной функции f(t) и интегральной функции F(t) при выравнивании по ЗНР и по ЗРВ представлено на рисунке 1.1 и 1.2 в приложении.
Таблица 1.4 – Значения f(t) и F(t) при ЗРВ
| Интервалы, мм | 6,00-6,16 | 6,16-6,32 | 6,32-6,48 | 6,48-6,64 | 6,64-6,80 | 6,80-6,96 |
| f(t) | 0,083 | 0,183 | 0,247 | 0,234 | 0,15 | 0,069 |
| F(t) | 0,096 | 0,243 | 0,536 | 0,719 | 0,902 | 0,969 |
1.7 Критерии согласия опытных и теоретических распределений показателей надежности
Применительно к показателям надежности тракторов и сельскохозяйственных машин, чаще используется критерий согласия Пирсона χ2.
Критерий χ2 определяется по формуле:
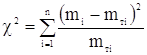 , (1.23)
, (1.23)
где n – число интервалов в статистическом ряду;
mi – опытная частота в i-ом интервале;
mтi – теоретическая частота в i-ом интервале.
![]() (1.24)
(1.24)
Для определения критерия согласия χ2 нужно иметь статистический ряд, который удовлетворяет условиям:
![]()
![]() . (1.25)
. (1.25)
В случае, если статистический ряд не удовлетворяет этим условиям, проводится укрупнение его путем объединения интервалов с частотой mi или mтi меньше 5 с соседними.
Для данного задания значение теоретической частоты (mтi) для каждого интервала статистического ряда, определенное по формуле 1.24 для ЗНР и ЗРВ представлено в таблице 1.5.
Таблица 1.5 – Значение теоретической частоты для ЗНР и ЗРВ
| Интервалы, мм | 6,00-6,16 | 6,16-6,32 | 6,32-6,48 | 6,48-6,64 | 6,64-6,80 | 6,80-6,96 | |
| Опытная частота mi | 3 | 5 | 6 | 7 | 6 | 3 | |
| F (t) | ЗНР | 0,085 | 0,239 | 0,484 | 0,732 | 0,902 | 0,975 |
| ЗРВ | 0,096 | 0,243 | 0,536 | 0,719 | 0,902 | 0,969 | |
| Теоретическая частота, mтi | ЗНР | 2,55 | 4,62 | 7,35 | 7,44 | 5,1 | 2,19 |
| ЗРВ | 2,88 | 4,41 | 8,79 | 5,49 | 5,49 | 2,01 | |
Так как при выравнивании по ЗНР статистический ряд не удовлетворяет условию 1.25, производим укрупнение статистического ряда, т.е. объединяем первый и второй, а также пятый и шестой интервалы. Укрупненный статистический ряд представлен в таблице 1.6.
Таблица 1.6 – Укрупненный статистический ряд для определения критерия согласия χ2
| Интервалы, мм | 6,00-6,32 | 6,32-6,48 | 6,48-6,64 | 6,64-6,96 | |
| Опытная частота, mi | 8 | 6 | 7 | 9 | |
| Теоретическая частота, mтi | ЗНР | 7,17 | 7,35 | 7,44 | 7,29 |
| ЗРВ | 7,29 | 8,79 | 5,49 | 7,5 | |
Критерий χ2 будет соответственно равен:
- для закона нормального закона
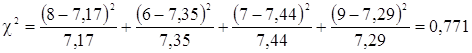 .
.
- для закона распределения Вейбулла
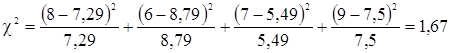 .
.
Для количественной оценки совпадения опытного и теоретического распределения определяется вероятность совпадения по критерию Пирсона Р(χ2), определяемая по таблицам в литературных источниках.
Вероятность совпадения при прочих равных условиях зависит также от повторности исследуемой информации. Для пользования таблицей необходимо определить число степеней свободы "r" по уравнению:
![]() (1.26)
(1.26)
где ny – число интервалов укрупненного статистического ряда;
к – число параметров теоретического закона распределения;
1 – связь, накладываемая закономерностью ∑Pi=1.
Для данного примера ![]()
Тогда для закона нормального распределения Р(χ2) = 40%, для закона распределения Вейбулла Р(χ2) = 20%.
Принято считать, что теоретический закон согласуется с опытным распределением, если Р(χ2)≥10%.
Из проведенной проверки следует, что оба теоретические закона согласуются с опытным распределением, но вероятность совпадения закона нормального распределения несколько выше, чем закон распределения Вейбулла.
Похожие работы
... на регулирующие воздействия, определив перечень параметров, необходимых при этом. Обработка информации при разработке нефтяных месторождений наиболее эффективно проводится в условиях автоматизированных систем. В процессе автоматизированной обработки информации при решении задач проектирования, анализа и управления процессом разработки нефтяных месторождений последовательно возникают и решаются ...
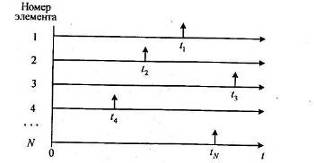
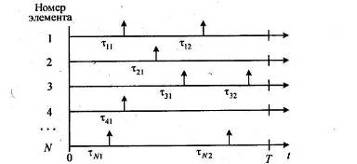
... 1.2. Временная диаграмма моментов отказов восстанавливаемых элементов с известными номерами Второй способ регистрации отказов, очевидно, сводится к первому, если фиксируются номера отказавших элементов. В качестве статистических данных берется совокупность разностей τi,j, представляющих собой времена работы элементов до первого отказа. · Третий способ регистрации Элементы, поставленные ...
... его увеличением для целей информационного обеспечения исполнительных местных органов [7,8]. 3 ОПЫТ УПРАВЛЕНИЯ И ОБОЩЕНИЕ ДАННЫХ НА ПРИМЕРЕ АЛМАТИНСКОГО ОБЛАСТНОГО УПРАВЛЕНИЯ СТАТИСТИКИ3.1 Алматинское областное управление статистики как субъект сбора и обобщения статистической информации В своей деятельности Алматинское областное управление статистики (АОУС) руководствуется ...
... , и обеспеченном необходимыми средствами испытаний. К эксплуатационным относятся испытания, проводимые для определения (оценки) показателей надежности в заданных режимах и условиях эксплуатации. Организация определительных испытаний на надёжность Определительные испытания на надёжность могут проводиться по разным планам. Каждый план имеет некоторое количество параметров, для каждого из ...
0 комментариев