Статистический ряд информации
Проверка информации на выпадающие точки
Определение коэффициента вариации
Зная параметры "а" и "в" и пользуясь табулированными функциями аf(t) и F(t), можно определить дифференциальную и интегральную функции
Определение доверительных границ рассеивания одиночного и среднего значений показателя надежности. Абсолютная и относительная предельные ошибки
Определение минимального числа объектов наблюдения при оценке показателей надежности
Нанести опытные точки на график и через них провести прямую линию таким образом, чтобы точки были максимально приближены к этой прямой
Продолжить график до пересечения с осью абсцисс и найти отрезок "Б". По отрезку определяем параметр "в"
Навигация
Определение доверительных границ рассеивания одиночного и среднего значений показателя надежности. Абсолютная и относительная предельные ошибки
Обработка статистической информации при определении показателей надежности
30463
знака
8
таблиц
0
изображений
1.8 Определение доверительных границ рассеивания одиночного и среднего значений показателя надежности. Абсолютная и относительная предельные ошибки
Доверительные границы рассеивания показателей надежности при использовании закона нормального распределения определяется по формулам:
а) для одиночного значения показателя надежности
; (1.27)
; (1.28)
; (1.29)
, (1.30)
где 
- нижняя доверительная граница одиночного значения показателя надежности;
- верхняя доверительная граница одиночного значения показателя надежности;
σ – среднее квадратическое отклонение;
- коэффициент Стьюдента определяется по таблице в зависимости от принятой доверительной вероятности α и объема информации N;
- доверительный интервал;
- абсолютная ошибка рассеивания.
б) для среднего значения показателя надежности:
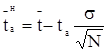; (1.31)
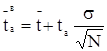; (1.32)
; (1.33)
, (1.34)
где - 
- нижняя доверительная граница рассеивания среднего значения показателя надежности;
- верхняя доверительная граница рассеивания среднего значения показателя надежности;
- абсолютная ошибка рассеивания среднего значения показателя надежности.
Относительная ошибка переноса опытных значений показателя надежности на генеральную совокупность:
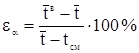(1.35)
Определяем доверительные границы рассеивания одиночного и среднего значений показателя надежности, предварительно задаемся доверительной вероятностью α = 0,95. По таблице определяем значение коэффициента Стьюдента для α = 0,95 и N = 30. Для заданных условий = 2,04. Тогда, по формулам 1.27, 1.28, 1.30 и 1.31 определим:
мм;
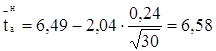мм;
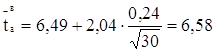мм;
мм;
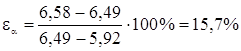
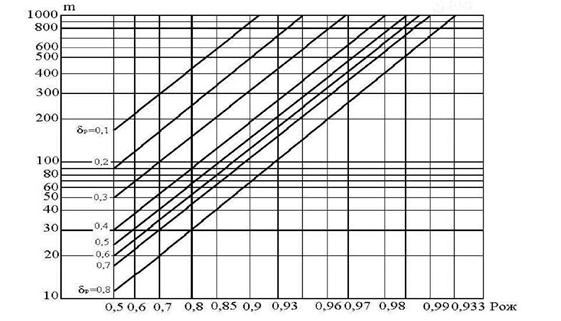
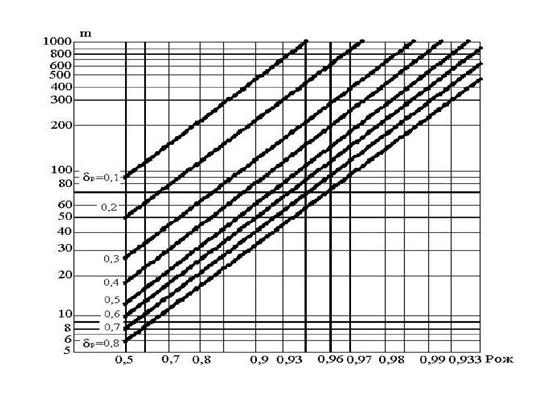
Расчет доверительных границ рассеивания при использовании закона распределения Вейбулла ведется от нуля, т.к. кривая распределения в этом случае асимметрична.
Рассеивание одиночных значений показателя надежности определяется по формулам:
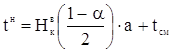, (1.36)
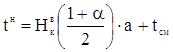(1.37)
где tн – нижняя доверительная граница;
tв – верхняя доверительная граница;
– нормированная квантиль закона распределения Вейбулла, определяется по таблице из литературных источников для известных значений "в" и 
;
а – параметр распределения Вейбулла.
Для определения границ рассеивания среднего значения используются формулы:
, (1.38)
, (1.39)
где 
– нижняя доверительная граница;
– верхняя доверительная граница;
r1; r3 – коэффициенты Вейбулла, определяются по таблице из литературы;
в – параметр распределения Вейбулла.
При доверительной вероятности α=0,95; 
=6,49 мм; tсм=5,92 мм; в=2,5; а=0,63 мм доверительные границы рассеивания одиночного и среднего значения определенные по формулам 1.21…1.24 будут равны:
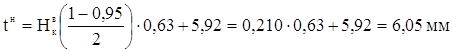
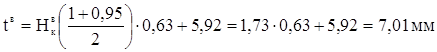
Относительная ошибка рассеивания (переноса) опытных значений показателя надежности на генеральную совокупность:
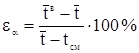(1.40)
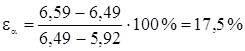
Похожие работы
... на регулирующие воздействия, определив перечень параметров, необходимых при этом. Обработка информации при разработке нефтяных месторождений наиболее эффективно проводится в условиях автоматизированных систем. В процессе автоматизированной обработки информации при решении задач проектирования, анализа и управления процессом разработки нефтяных месторождений последовательно возникают и решаются ...
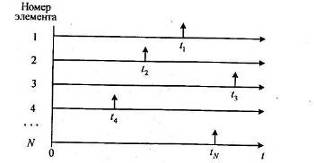
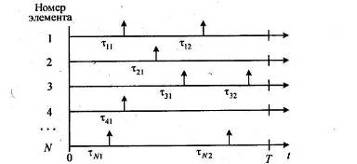
... 1.2. Временная диаграмма моментов отказов восстанавливаемых элементов с известными номерами Второй способ регистрации отказов, очевидно, сводится к первому, если фиксируются номера отказавших элементов. В качестве статистических данных берется совокупность разностей τi,j, представляющих собой времена работы элементов до первого отказа. · Третий способ регистрации Элементы, поставленные ...
... его увеличением для целей информационного обеспечения исполнительных местных органов [7,8]. 3 ОПЫТ УПРАВЛЕНИЯ И ОБОЩЕНИЕ ДАННЫХ НА ПРИМЕРЕ АЛМАТИНСКОГО ОБЛАСТНОГО УПРАВЛЕНИЯ СТАТИСТИКИ3.1 Алматинское областное управление статистики как субъект сбора и обобщения статистической информации В своей деятельности Алматинское областное управление статистики (АОУС) руководствуется ...
... , и обеспеченном необходимыми средствами испытаний. К эксплуатационным относятся испытания, проводимые для определения (оценки) показателей надежности в заданных режимах и условиях эксплуатации. Организация определительных испытаний на надёжность Определительные испытания на надёжность могут проводиться по разным планам. Каждый план имеет некоторое количество параметров, для каждого из ...
0 комментариев